冀教版九年级下册31.3用频率估计概率课件(共19张ppt)
文档属性
| 名称 | 冀教版九年级下册31.3用频率估计概率课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 438.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览





文档简介
用频率估计概率
我们知道, 抛掷一枚均匀硬币, 硬币落地后, 出现“正面朝上”的可能性和“反面朝上”的可能性是一样的, 即“正面朝上”的概率和“反面朝上”的概率都是 .在实际掷硬币时, 会出现什么情况?若只抛一次说明不了什么问题, 我们不妨多抛掷几次试试.
(1) 抛掷一枚均匀硬币400次,每隔50次,
分别记录“正面朝上”和“反面朝上”的
次数, 汇总数据后, 完成下表:
{8A107856-5554-42FB-B03E-39F5DBC370BA}累计抛
掷次数
50
100
150
200
250
300
350
400
"正面朝上"的频数
"正面朝上"的频率
做一做
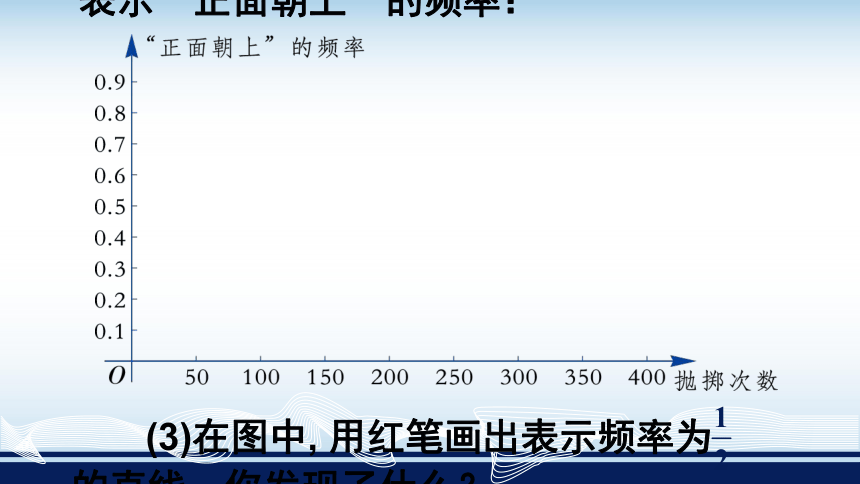
(2)根据上表的数据,在图中画折线统计图表示“正面朝上”的频率:
(3)在图中, 用红笔画出表示频率为 的直线,你发现了什么?
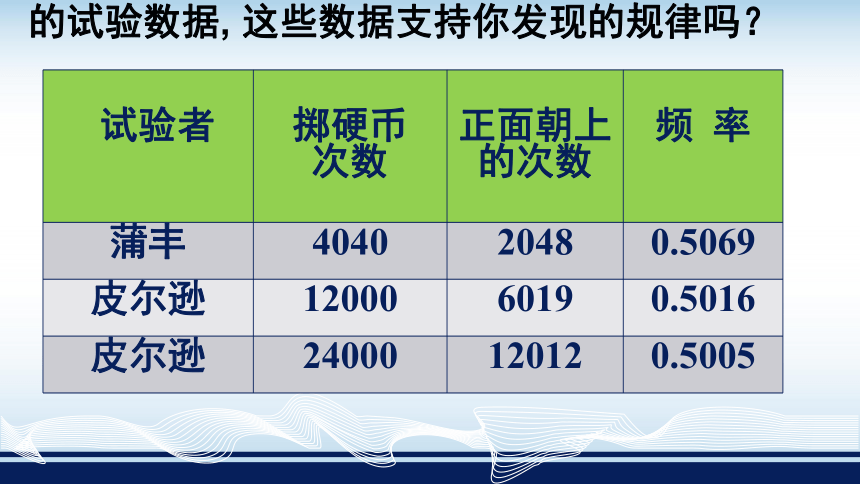
(4)下表是历史上一些数学家所做的掷硬币的试验数据, 这些数据支持你发现的规律吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
试验者
掷硬币
次数
正面朝上的次数
频 率
蒲丰
4040
2048
0.5069
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
看来用频率估计硬币出现 “正面朝上” 的概率是合理的.
可以看出,随着掷硬币次数的增加,“正面朝上”的频率稳定在 左右.
上面的例子说明,通过大量重复试验,
可以用随机事件发生的频率来估计该事件
发生的概率.
对于掷硬币试验,它的所有可能结果
只有两个,而且出现两种可能结果的可能性相等,而对于一般的随机事件,当试验所有的可能结果不是有限个,或者各种可能结果发生的可能性不相等时,就不能用4.2节的方法来求概率. 频率是否可以估计该随机事件的概率呢?
我们再来做一个抛瓶盖试验.
做一做
在一块平整地板上抛掷一个矿泉水瓶盖,
瓶盖落地后有两种可能情况:“开口朝上”
和“开口不朝上”. 由于瓶盖头重脚轻,上下
不对称,“开口朝上”和“开口不朝上”的
可能性一样吗? 如果不一样,出现哪种情况
的可能性大一些?我们借助重复试验来解决
这个问题.
(1) 全班同学分成6组,每组同学依次抛掷
瓶盖80次,观察瓶盖着地时的情况,并根据全班
试验结果填写下表:
{8A107856-5554-42FB-B03E-39F5DBC370BA}
累计抛掷
次数
80
160
240
320
400
480
“开口朝上”的频数
“开口朝上”的频率
(2) 根据上表中的数据,在图中画折线
统计表示“开口朝上”的频率.
(3) 观察“开口朝上”的频率分布图,
随着抛掷次数的增加,“开口朝上”的频率
是如何变化的?
(4) 该试验中,是“开口朝上”的可能性
大还是“开口不朝上”的可能性大?
研究随机现象与随机事件的基本方法就是重复地对现象进行观察,在n次观察中,如果某个随机事件发生了m次,则在这n次观察中
这个事件发生的频率为 如果随机事件发生
的概率(即可能性)大,则它在多次的重复观察中出现的次数就越多,因而其频率就大,所以频率在一定程度上也反映了随机事件的可能性的大小.
可以发现,在抛瓶盖试验中,“开口朝上”
的频率 一般会随着抛掷次数的增加, 稳定
在某个常数p 附近. 这个常数就是“开口朝上”发生的可能性.即事件“开口朝上”的概率.
所以在大量重复试验中, 如果事件A发生的频率为 ,那么用 作为事件A发生的概率的估计是合理的.
在抛瓶盖试验中,“开口朝上”的频率稳定于哪一个数值?你能估计出瓶盖“开口朝上”
的概率吗?
需要指出的是,频率和概率都是随机事件
可能性大小的定量的刻画,但频率与试验次数
及具体的试验有关,因此频率具有随机性;而
概率是刻画随机事件发生可能性大小的数值,
是一个固定的量, 不具有随机性.因此, 掷100次
硬币并不一定能得到“正面朝上”的频率是
和“反面朝上”的频率是
例 瓷砖生产受烧制时间、温度、材质的
影响, 一块砖坯放在炉中烧制, 可能成为合格品,
也可能成为次品或废品, 究竟发生哪种结果, 在
烧制前无法预知, 所以这是一种随机现象, 而
烧制的结果是“合格品”是一个随机事件, 这个事件的概率称为“合格品率”.由于烧制结果
不是等可能的,我们常用“合格品”的频率
作为“合格品率”的估计.
范例分析
{8A107856-5554-42FB-B03E-39F5DBC370BA}
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品频率
某瓷砖厂对最近出炉的一大批某型号瓷砖
进行质量抽检,结果如下:
(1) 计算上表中合格品的各频率(精确到0.001);
(2) 估计这种瓷砖的合格品率(精确到0.01);
(3) 若该工厂本月生产该型号瓷砖500000块,
试估计合格品数.
解
(1)逐项计算,填表如下:
0.960
0.950
0.957
0.963
0.962
0.962
0.963
0.961
0.962
(2) 观察上表,可以发现, 当抽取的瓷砖数n≥400时,合格品频率稳定在0.962的附近,所以我们可取p=0.96作为该型号瓷砖的合格品率的估计.
练习
如图是一个能自由转动的转盘,盘面被分成
8个相同的扇形,颜色分为红、黄、蓝3种.转盘的指针固定,让转盘自由转动,当它停止后,记下指针指向的颜色.如此重复做50次,把结果记录在下表中:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
红色
黄色
蓝色
频 数
频 率
(3) 500000×96%=480000(块),
可以估计该型号合格品数为480000块.
(1) 试估计当圆盘停下来时,指针指向黄色
的概率是多少?
(2) 如果自由转动圆盘240次, 那么指针指向
黄色的次数大约是多少?
我们知道, 抛掷一枚均匀硬币, 硬币落地后, 出现“正面朝上”的可能性和“反面朝上”的可能性是一样的, 即“正面朝上”的概率和“反面朝上”的概率都是 .在实际掷硬币时, 会出现什么情况?若只抛一次说明不了什么问题, 我们不妨多抛掷几次试试.
(1) 抛掷一枚均匀硬币400次,每隔50次,
分别记录“正面朝上”和“反面朝上”的
次数, 汇总数据后, 完成下表:
{8A107856-5554-42FB-B03E-39F5DBC370BA}累计抛
掷次数
50
100
150
200
250
300
350
400
"正面朝上"的频数
"正面朝上"的频率
做一做
(2)根据上表的数据,在图中画折线统计图表示“正面朝上”的频率:
(3)在图中, 用红笔画出表示频率为 的直线,你发现了什么?
(4)下表是历史上一些数学家所做的掷硬币的试验数据, 这些数据支持你发现的规律吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
试验者
掷硬币
次数
正面朝上的次数
频 率
蒲丰
4040
2048
0.5069
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
看来用频率估计硬币出现 “正面朝上” 的概率是合理的.
可以看出,随着掷硬币次数的增加,“正面朝上”的频率稳定在 左右.
上面的例子说明,通过大量重复试验,
可以用随机事件发生的频率来估计该事件
发生的概率.
对于掷硬币试验,它的所有可能结果
只有两个,而且出现两种可能结果的可能性相等,而对于一般的随机事件,当试验所有的可能结果不是有限个,或者各种可能结果发生的可能性不相等时,就不能用4.2节的方法来求概率. 频率是否可以估计该随机事件的概率呢?
我们再来做一个抛瓶盖试验.
做一做
在一块平整地板上抛掷一个矿泉水瓶盖,
瓶盖落地后有两种可能情况:“开口朝上”
和“开口不朝上”. 由于瓶盖头重脚轻,上下
不对称,“开口朝上”和“开口不朝上”的
可能性一样吗? 如果不一样,出现哪种情况
的可能性大一些?我们借助重复试验来解决
这个问题.
(1) 全班同学分成6组,每组同学依次抛掷
瓶盖80次,观察瓶盖着地时的情况,并根据全班
试验结果填写下表:
{8A107856-5554-42FB-B03E-39F5DBC370BA}
累计抛掷
次数
80
160
240
320
400
480
“开口朝上”的频数
“开口朝上”的频率
(2) 根据上表中的数据,在图中画折线
统计表示“开口朝上”的频率.
(3) 观察“开口朝上”的频率分布图,
随着抛掷次数的增加,“开口朝上”的频率
是如何变化的?
(4) 该试验中,是“开口朝上”的可能性
大还是“开口不朝上”的可能性大?
研究随机现象与随机事件的基本方法就是重复地对现象进行观察,在n次观察中,如果某个随机事件发生了m次,则在这n次观察中
这个事件发生的频率为 如果随机事件发生
的概率(即可能性)大,则它在多次的重复观察中出现的次数就越多,因而其频率就大,所以频率在一定程度上也反映了随机事件的可能性的大小.
可以发现,在抛瓶盖试验中,“开口朝上”
的频率 一般会随着抛掷次数的增加, 稳定
在某个常数p 附近. 这个常数就是“开口朝上”发生的可能性.即事件“开口朝上”的概率.
所以在大量重复试验中, 如果事件A发生的频率为 ,那么用 作为事件A发生的概率的估计是合理的.
在抛瓶盖试验中,“开口朝上”的频率稳定于哪一个数值?你能估计出瓶盖“开口朝上”
的概率吗?
需要指出的是,频率和概率都是随机事件
可能性大小的定量的刻画,但频率与试验次数
及具体的试验有关,因此频率具有随机性;而
概率是刻画随机事件发生可能性大小的数值,
是一个固定的量, 不具有随机性.因此, 掷100次
硬币并不一定能得到“正面朝上”的频率是
和“反面朝上”的频率是
例 瓷砖生产受烧制时间、温度、材质的
影响, 一块砖坯放在炉中烧制, 可能成为合格品,
也可能成为次品或废品, 究竟发生哪种结果, 在
烧制前无法预知, 所以这是一种随机现象, 而
烧制的结果是“合格品”是一个随机事件, 这个事件的概率称为“合格品率”.由于烧制结果
不是等可能的,我们常用“合格品”的频率
作为“合格品率”的估计.
范例分析
{8A107856-5554-42FB-B03E-39F5DBC370BA}
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品频率
某瓷砖厂对最近出炉的一大批某型号瓷砖
进行质量抽检,结果如下:
(1) 计算上表中合格品的各频率(精确到0.001);
(2) 估计这种瓷砖的合格品率(精确到0.01);
(3) 若该工厂本月生产该型号瓷砖500000块,
试估计合格品数.
解
(1)逐项计算,填表如下:
0.960
0.950
0.957
0.963
0.962
0.962
0.963
0.961
0.962
(2) 观察上表,可以发现, 当抽取的瓷砖数n≥400时,合格品频率稳定在0.962的附近,所以我们可取p=0.96作为该型号瓷砖的合格品率的估计.
练习
如图是一个能自由转动的转盘,盘面被分成
8个相同的扇形,颜色分为红、黄、蓝3种.转盘的指针固定,让转盘自由转动,当它停止后,记下指针指向的颜色.如此重复做50次,把结果记录在下表中:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
红色
黄色
蓝色
频 数
频 率
(3) 500000×96%=480000(块),
可以估计该型号合格品数为480000块.
(1) 试估计当圆盘停下来时,指针指向黄色
的概率是多少?
(2) 如果自由转动圆盘240次, 那么指针指向
黄色的次数大约是多少?
