人教版八年级上册第14章 整式乘除与因式分解 第3课时 用完全平方公式分解因式课件(24张PPT)
文档属性
| 名称 | 人教版八年级上册第14章 整式乘除与因式分解 第3课时 用完全平方公式分解因式课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 444.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:15:41 | ||
图片预览








文档简介
第十四章 整式的乘法与因式分解
14.3 因式分解
第3课时 用完全平方公式分解因式
我们把a?+2ab+b?和a?-2ab+b?这样的式子叫作完全平方式.
精彩回放
区分特征
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
1.两个数的平方和加上这两个数的_________________,等于这两个数的____的平方.用字母表示为a2+2ab+b2=______________.
2.两个数的平方和减去这两个数的______________,等于这两个数的______的平方.用字母表示为a2-2ab+b2=_______________.
3.像a2+2ab+b2,a2-2ab+b2这样的式子叫做__________________.
积的2倍
和
(a+b)2
积的2倍
差
(a-b)2
完全平方式
基础检测
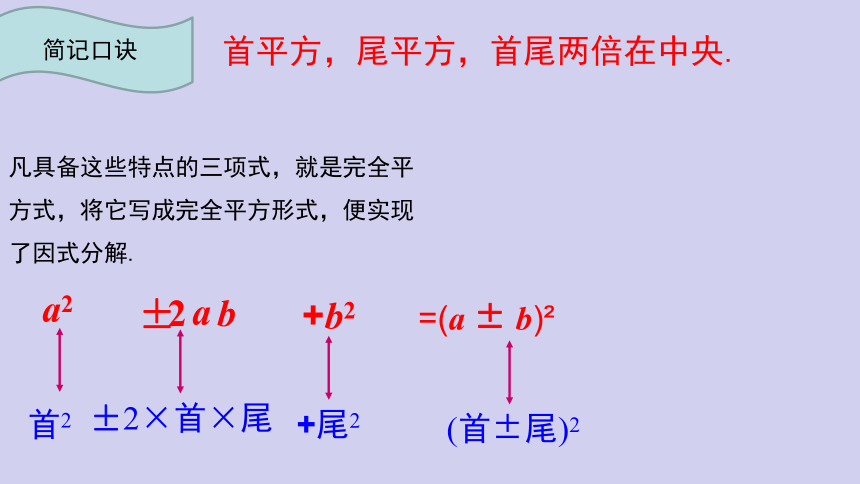
简记口诀 首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
简记口诀
精彩演示
分解因式:
16x2+24x+9;
分析: 16x2=(4x)2, 9=3?,24x=2·4x·3, 所以16x2+24x+9是一个完全平方式,
即16x2 + 24x +9= (4x)2+ 2·4x·3 + (3)2.
2
a
b
+b2
a2
1.(6分)分解因式:
(1) x2+2x+1=__________________;
(2) x2-4x+4=_______________;
(3) 3x2-18x+27=_________________.
(x+1)2
(x-2)2
3(x-3)2
实际演练
3.a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
2.m?-6m+9=( )? - 2· ( ) ·( )+( )? =( )?
1. x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a?±2ab+b?=(a±b)?,填空:
m
m - 3
3
x
2
m
3
1.下列四个多项式中,能因式分解的是( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
2.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
B
完全平方式
3.(3分)下列式子中是完全平方式的是( )
A.a2+ab+b2 B.a2+2a+2
C.a2-2b+b2 D.a2+2a+1
4.(2分)若x2+2(m-3)x+16是完全平方式,则m的值为______________.
5.(2分)已知9x2-12xy+m是一个完全平方式,则m=________.
D
7或-1
4y2
利用完全平方公式分解因式
6.(3分)下列各式中可以用完全平方公式分解因式的是( )
A.m2-mn+n2 B.(a+b)2-4ab
C.x2-2x+4 D.x2+2x-1
7.(3分)(长春中考)把多项式x2-6x+9分解因式,结果正确的是( )
A.(x-3)2 B.(x-9)2
C.(x+3)(x-3) D.(x+9)(x-9)
B
A
8.若m=2n+1,则m2-4mn+4n2的值是________.
1
9.若关于x的多项式x2-8x+m2是完全平方式,则m的值为___________ .
±4
10.把下列多项式因式分解.
(1)x2-12x+36; (2)4(2a+b)2-4(2a+b)+1;
(2)原式=[2(2a+b)]? - 2·2(2a+b)·1+(1)?
=(4a+2b - 1)2;
解:(1)原式 =x2-2·x·6+(6)2
=(x-6)2;
11.(2分)利用完全平方公式计算:
2×1012+2×101×98+2×492=________________.
12.(8分)把下列各式因式分解:
(1)4x2+y2-4xy;
解:原式=(2x-y)2
(2)9-12a+4a2;
解:原式=(3-2a)2
45 000
(3)x3-6x2+9x;
解:原式=x(x-3)2
(4)(m+n)2-6(m+n)+9.
解:原式=(m+n-3)2
(2)原式
12.计算:(1)38.92-2×38.9×48.9+48.92.
解:(1)原式=(38.9-48.9)2
=100.
13.(8分)(1)已知a-b=3,求a(a-2b)+b2的值;
解:原式=a2-2ab+b2=(a-b)2,当a-b=3时,原式=32=9
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
解:原式=ab(a2+2ab+b2)=ab(a+b)2.当ab=2,a+b=5时,原式=2×52=50
14、选择题(每小题4分,共16分)
1.(漯河月考)已知x2+16x+k是完全平方式,则常数k等于( )
A.64 B.48 C.32 D.16
2.把多项式a2-2ab+b2-1分解因式,结果是( )
A.(a-b+1)(a-b-1)
B.(a-b+1)(a+b-1)
C.(a+b+1)(a+b-1)
D.(a+b+1)(a-b-1)
A
A
3.多项式4x2+1加上一个数或单项式后,使它成为一个整式的完全平方式,那么加上的数或单项式可以从①-1;②4x;③-4x;④4x4中选取( )
A.② B.③
C.②③ D.①②③④
4.在△ABC中,已知三边a,b,c满足a4+2a2b2+b4-2a3b-2ab3=0,则△ABC的形状是( )
A.等腰三角形 B.等腰直角三角形
C.等边三角形 D.直角三角形
D
A
15、填空题(每小题4分,共8分)
1.若a+b=3,则2a2+4ab+2b2-6的值为____.
2.若A=(2 019-1 985)2,B=(2 019-1 985)(2 018-1 986),C=(2 018-1 986)2,则A+C-2B的值为____.
12
4
三、解答题(共36分)
16.(16分)分解因式:
(1)4a2-b2+2b-1;
解:原式=(2a+b-1)(2a-b+1)
(2)x2-1-2ax+a2;
解:原式=(x-a+1)(x-a-1)
(3)(a2-b2)+4(b-1);
解:原式=(a+b-2)(a-b+2)
(4)x2-xy+4x-4y.
解:原式=(x+4)(x-y)
17 (1)已知a-b=3,求a(a-2b)+b2的值;
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
原式=2×52=50.
解:(1)原式=a2-2ab+b2=(a-b)2.
当a-b=3时,原式=32=9.
(2)原式=ab(a2+2ab+b2)=ab(a+b)2.
当ab=2,a+b=5时,
18.(10分)若|m+4|与n2-2n+1互为相反数,把多项式x2+4y2-mxy-n分解因式.
解:由题意有|m+4|+(n2-2n+1)=0,即|m+4|+(n-1)2=0,∴m=-4,n=1.∴x2+4y2-mxy-n=x2+4y2+4xy-1=(x+2y)2-12=(x+2y+1)(x+2y-1)
【综合运用】
19.(10分)阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq,得x2+(p+q)x+pq=(x+p)(x+q).
利用这个式子可以将某些二次项系数是1的二次三项式分解因式.
例如:将式子x2+3x+2分解因式.
分析:这个式子的常数项2=1×2,一次项系数3=1+2,所以x2+3x+2=x2+(1+2)x+1×2.
解:x2+3x+2=(x+1)(x+2).
请仿照上面的方法,解答下列问题:
(1)分解因式:x2+7x-18=___________________;
(2)利用因式分解法解方程:x2-6x+8=0;
(3)填空:若x2+px-8可分解为两个一次因式的积,则整数p的所有可能值是_________________.
解:(2)方程分解得(x-2)(x-4)=0,可得x-2=0或x-4=0,解得x=2或x=4 (3)-8=-1×8,-8=-8×1,-8=-2×4,-8=-4×2.∵-1+8=7,-8+1=-7,-2+4=2,-4+2=-2,∴p的可能值为±7或±2
(x-2)(x+9)
±7或±2
14.3 因式分解
第3课时 用完全平方公式分解因式
我们把a?+2ab+b?和a?-2ab+b?这样的式子叫作完全平方式.
精彩回放
区分特征
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
1.两个数的平方和加上这两个数的_________________,等于这两个数的____的平方.用字母表示为a2+2ab+b2=______________.
2.两个数的平方和减去这两个数的______________,等于这两个数的______的平方.用字母表示为a2-2ab+b2=_______________.
3.像a2+2ab+b2,a2-2ab+b2这样的式子叫做__________________.
积的2倍
和
(a+b)2
积的2倍
差
(a-b)2
完全平方式
基础检测
简记口诀 首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
简记口诀
精彩演示
分解因式:
16x2+24x+9;
分析: 16x2=(4x)2, 9=3?,24x=2·4x·3, 所以16x2+24x+9是一个完全平方式,
即16x2 + 24x +9= (4x)2+ 2·4x·3 + (3)2.
2
a
b
+b2
a2
1.(6分)分解因式:
(1) x2+2x+1=__________________;
(2) x2-4x+4=_______________;
(3) 3x2-18x+27=_________________.
(x+1)2
(x-2)2
3(x-3)2
实际演练
3.a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
2.m?-6m+9=( )? - 2· ( ) ·( )+( )? =( )?
1. x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a?±2ab+b?=(a±b)?,填空:
m
m - 3
3
x
2
m
3
1.下列四个多项式中,能因式分解的是( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
2.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
B
完全平方式
3.(3分)下列式子中是完全平方式的是( )
A.a2+ab+b2 B.a2+2a+2
C.a2-2b+b2 D.a2+2a+1
4.(2分)若x2+2(m-3)x+16是完全平方式,则m的值为______________.
5.(2分)已知9x2-12xy+m是一个完全平方式,则m=________.
D
7或-1
4y2
利用完全平方公式分解因式
6.(3分)下列各式中可以用完全平方公式分解因式的是( )
A.m2-mn+n2 B.(a+b)2-4ab
C.x2-2x+4 D.x2+2x-1
7.(3分)(长春中考)把多项式x2-6x+9分解因式,结果正确的是( )
A.(x-3)2 B.(x-9)2
C.(x+3)(x-3) D.(x+9)(x-9)
B
A
8.若m=2n+1,则m2-4mn+4n2的值是________.
1
9.若关于x的多项式x2-8x+m2是完全平方式,则m的值为___________ .
±4
10.把下列多项式因式分解.
(1)x2-12x+36; (2)4(2a+b)2-4(2a+b)+1;
(2)原式=[2(2a+b)]? - 2·2(2a+b)·1+(1)?
=(4a+2b - 1)2;
解:(1)原式 =x2-2·x·6+(6)2
=(x-6)2;
11.(2分)利用完全平方公式计算:
2×1012+2×101×98+2×492=________________.
12.(8分)把下列各式因式分解:
(1)4x2+y2-4xy;
解:原式=(2x-y)2
(2)9-12a+4a2;
解:原式=(3-2a)2
45 000
(3)x3-6x2+9x;
解:原式=x(x-3)2
(4)(m+n)2-6(m+n)+9.
解:原式=(m+n-3)2
(2)原式
12.计算:(1)38.92-2×38.9×48.9+48.92.
解:(1)原式=(38.9-48.9)2
=100.
13.(8分)(1)已知a-b=3,求a(a-2b)+b2的值;
解:原式=a2-2ab+b2=(a-b)2,当a-b=3时,原式=32=9
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
解:原式=ab(a2+2ab+b2)=ab(a+b)2.当ab=2,a+b=5时,原式=2×52=50
14、选择题(每小题4分,共16分)
1.(漯河月考)已知x2+16x+k是完全平方式,则常数k等于( )
A.64 B.48 C.32 D.16
2.把多项式a2-2ab+b2-1分解因式,结果是( )
A.(a-b+1)(a-b-1)
B.(a-b+1)(a+b-1)
C.(a+b+1)(a+b-1)
D.(a+b+1)(a-b-1)
A
A
3.多项式4x2+1加上一个数或单项式后,使它成为一个整式的完全平方式,那么加上的数或单项式可以从①-1;②4x;③-4x;④4x4中选取( )
A.② B.③
C.②③ D.①②③④
4.在△ABC中,已知三边a,b,c满足a4+2a2b2+b4-2a3b-2ab3=0,则△ABC的形状是( )
A.等腰三角形 B.等腰直角三角形
C.等边三角形 D.直角三角形
D
A
15、填空题(每小题4分,共8分)
1.若a+b=3,则2a2+4ab+2b2-6的值为____.
2.若A=(2 019-1 985)2,B=(2 019-1 985)(2 018-1 986),C=(2 018-1 986)2,则A+C-2B的值为____.
12
4
三、解答题(共36分)
16.(16分)分解因式:
(1)4a2-b2+2b-1;
解:原式=(2a+b-1)(2a-b+1)
(2)x2-1-2ax+a2;
解:原式=(x-a+1)(x-a-1)
(3)(a2-b2)+4(b-1);
解:原式=(a+b-2)(a-b+2)
(4)x2-xy+4x-4y.
解:原式=(x+4)(x-y)
17 (1)已知a-b=3,求a(a-2b)+b2的值;
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
原式=2×52=50.
解:(1)原式=a2-2ab+b2=(a-b)2.
当a-b=3时,原式=32=9.
(2)原式=ab(a2+2ab+b2)=ab(a+b)2.
当ab=2,a+b=5时,
18.(10分)若|m+4|与n2-2n+1互为相反数,把多项式x2+4y2-mxy-n分解因式.
解:由题意有|m+4|+(n2-2n+1)=0,即|m+4|+(n-1)2=0,∴m=-4,n=1.∴x2+4y2-mxy-n=x2+4y2+4xy-1=(x+2y)2-12=(x+2y+1)(x+2y-1)
【综合运用】
19.(10分)阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq,得x2+(p+q)x+pq=(x+p)(x+q).
利用这个式子可以将某些二次项系数是1的二次三项式分解因式.
例如:将式子x2+3x+2分解因式.
分析:这个式子的常数项2=1×2,一次项系数3=1+2,所以x2+3x+2=x2+(1+2)x+1×2.
解:x2+3x+2=(x+1)(x+2).
请仿照上面的方法,解答下列问题:
(1)分解因式:x2+7x-18=___________________;
(2)利用因式分解法解方程:x2-6x+8=0;
(3)填空:若x2+px-8可分解为两个一次因式的积,则整数p的所有可能值是_________________.
解:(2)方程分解得(x-2)(x-4)=0,可得x-2=0或x-4=0,解得x=2或x=4 (3)-8=-1×8,-8=-8×1,-8=-2×4,-8=-4×2.∵-1+8=7,-8+1=-7,-2+4=2,-4+2=-2,∴p的可能值为±7或±2
(x-2)(x+9)
±7或±2
