探索勾股定理

探索勾股定理（第一课时）
课型：探索新知 班级： 学习小组： 小组人姓名：
【 学习目标 】
通过自己动手操作，探索勾股定理。（难点）
会用勾股定理进行简单的计算，体会数形结合的思想。（重点）
将准备的4个全等的直角三角形拼成一个正方形,比比看谁拼的又快又好。
a、b、c分别表示直角三角形的三边，如图。
1.你能用不同的方法计算你所拼成的正方形的面积吗？
2.能不能根据面积找到a、b、c之间的等量关系呢？
你发现a、b、c之间的等量关系式是： 。
即：
公式变形为：
（1）
（2）
（3）
（4）
（5）
如图：受台风的影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
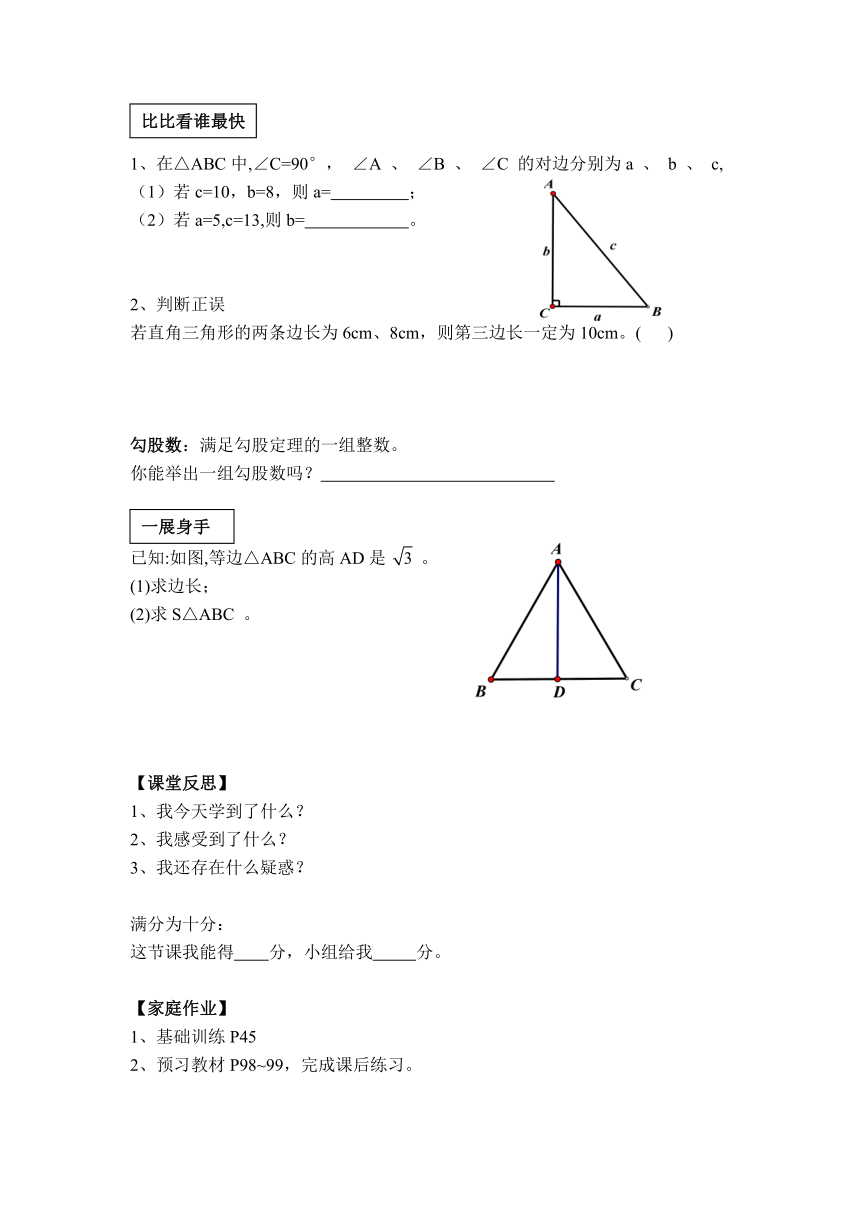
1、在△ABC中,∠C=90°， ∠A 、 ∠B 、 ∠C 的对边分别为a 、 b 、 c,
（1）若c=10，b=8，则a= ；
（2）若a=5,c=13,则b= 。
2、判断正误
若直角三角形的两条边长为6cm、8cm，则第三边长一定为10cm。( )
勾股数：满足勾股定理的一组整数。
你能举出一组勾股数吗？
已知:如图,等边△ABC的高AD是 。
(1)求边长；
(2)求S△ABC 。
【课堂反思】
我今天学到了什么？
我感受到了什么？
我还存在什么疑惑？
满分为十分：
这节课我能得 分，小组给我 分。
【家庭作业】
基础训练P45
预习教材P98~99，完成课后练习。
探索勾股定理（第二课时）
课型：预展结合课 班级： 学习小组： 小组人姓名：
【 学习目标 】
经历探索活动，了解勾股定理的逆定理。
会利用勾股定理的逆定理，判断一个三角形是否为直角三角形。
1勾股定理： 。
即： 。
2若直角三角形的两条直角边边长为5cm、12cm，那么斜边长是多少？
如图1，已知在△ABC中，AB=c,BC=a,AC=b,且a2+b2=c2,那么△ABC是直角三角形吗？
由此，我能得到直角三角形的判定定理：
如果 ；
那么这个三角形是直角三角形。
注意：1此定理是与勾股定理的联系是 ，我们称之为互逆定理。
这个定理又叫做： 。
2勾股定理的逆定理可以用来判定一个三角形是否为直角三角形。
1、若三角形的三边分别为4,4， ，则此三角形为 三角形。
2、如图，在△ABC中，已知AB=10，BD=6，AD=8，AC=17,求DC的长。
已知：如图AB=3，BC=12，CD=13，DA=4，AB⊥AD，试判断△BDC是否为直角三角形，并说明理由。
【课堂反思】
我今天学到了什么？
我感受到了什么？
我还存在什么疑惑？
满分为十分：
这节课我能得 分，小组给我 分。
【家庭作业】
1基础训练P46~47
A层：全做；B、C层：1~9；
2预习教材P99~100，完成课后练习。
比一比
提示：大正方形的面积有几种表示方法
算一算
这就是著名的“勾股定理”。
知识回归生活
比比看谁最快
一展身手
课堂抽测
测试下你的预习成果
学法指导：直角三角形的两直角边与斜边有什么关系？画一个Rt△,使它的两直角边分别为a、b,斜边为c，如图2.
图1
图2
牛刀小试