人教版八年级下册17.1 勾股定理第3课时课件(共16张ppt)
文档属性
| 名称 | 人教版八年级下册17.1 勾股定理第3课时课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
第十七章 勾股定理
17.1 勾股定理
第3课时
2、能在数轴上标出 、 、 等无理数。
1、理解勾股定理并能对无理数 : 、 、 、
、 等作出几何解释。
3、通过作图体会数形结合的思想。
重点:在数轴上标出无理数的点。
难点:理解尺规作图的原理。
1.已知直角三角形ABC的三边为a、b、c , ∠C= 90°,则 a、b、c 三者之间的关系是 ;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是 ;
3. 叫做无理数.
知识回顾
a2+b2=c2
无限不循环小数
问题思考
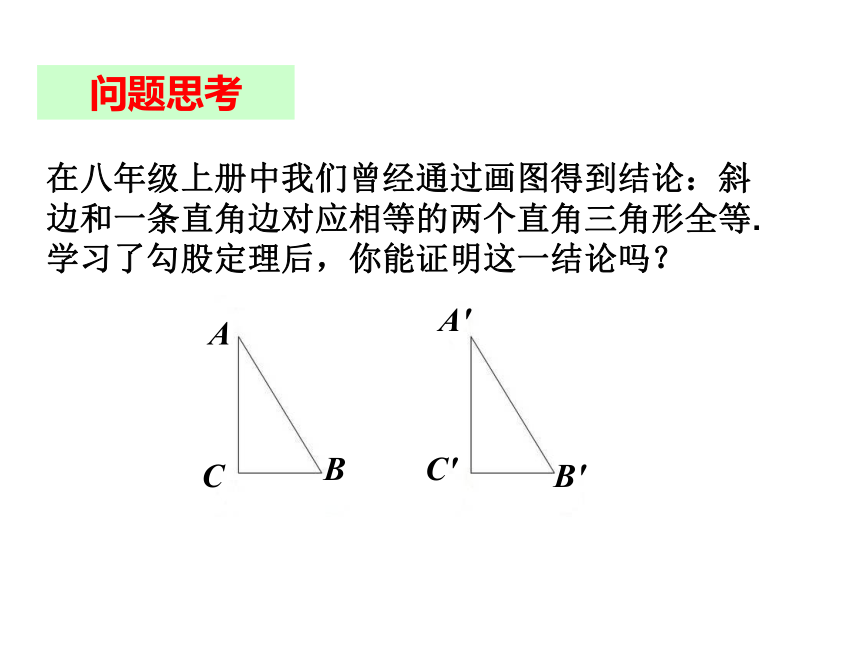
在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
B
A
C
C′
A′
B′
B
A
C
C′
A′
B′
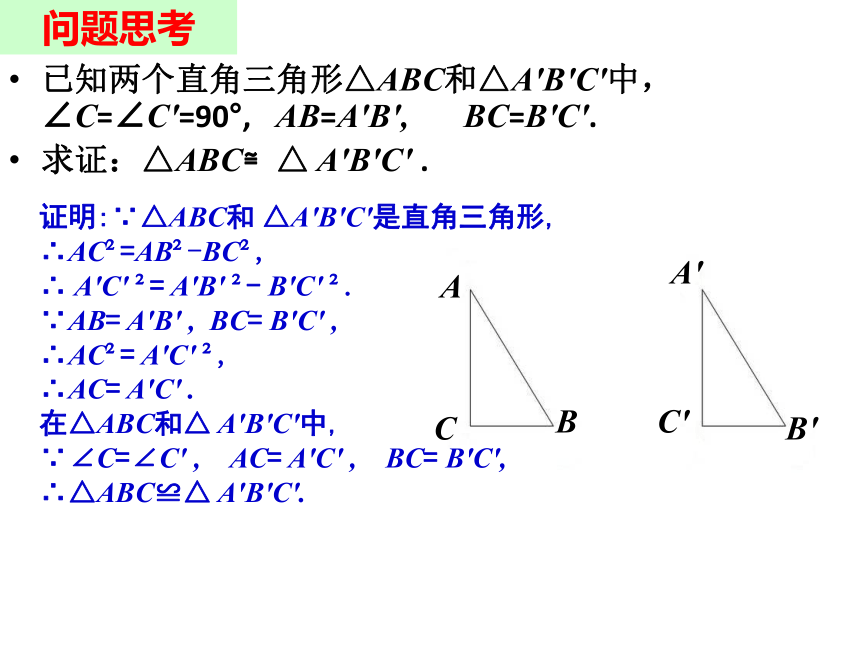
已知两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°,? AB=A′B′,? BC=B′C′.
求证:△ABC≌△ A′B′C′ .
问题思考
证明:∵△ABC和 △A′B′C′是直角三角形,
∴AC?=AB?-BC?,
∴ A′C′ ?= A′B′ ?- B′C′ ?.
∵AB= A′B′ ,?BC= B′C′ ,
∴AC?= A′C′ ?,
∴AC= A′C′ .
在△ABC和△ A′B′C′中,
∵∠C=∠C′ , AC= A′C′ , BC= B′C′,
∴△ABC≌△ A′B′C′.
?????????
实数
数轴上的点
一一对应
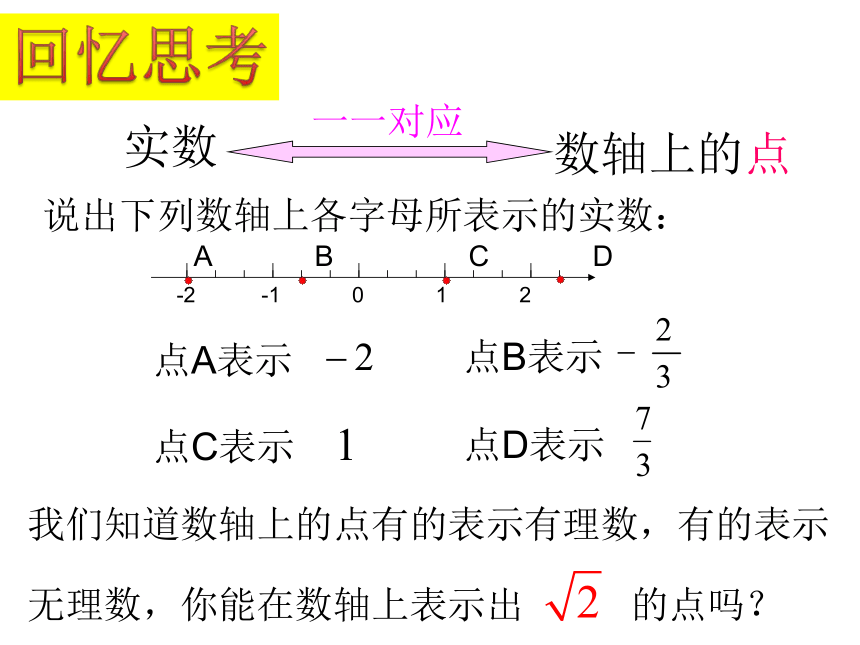
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?
-1 0 1 2 3
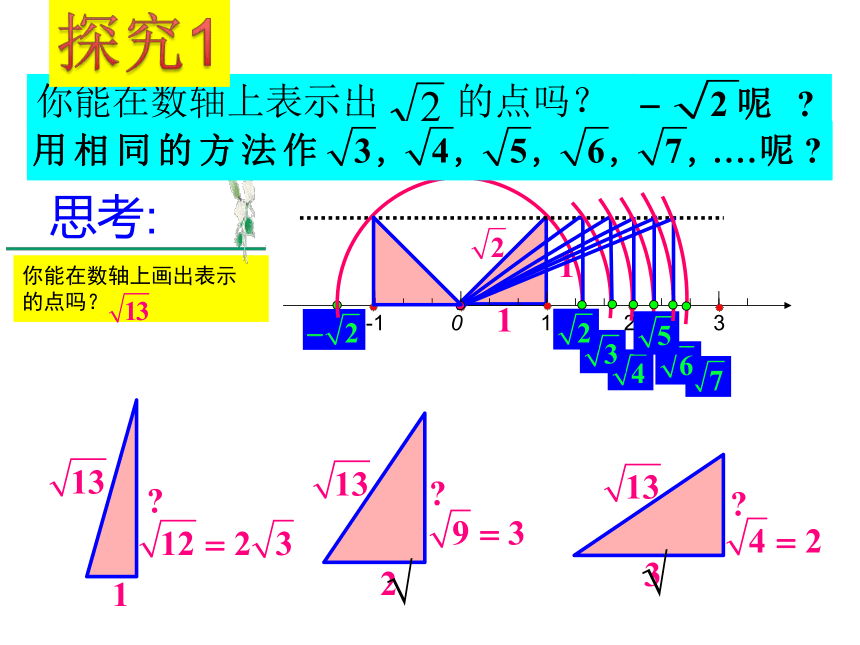
你能在数轴上表示出 的点吗?
你能在数轴上画出表示 的点吗?
思考:
√
√
探究二:你能在数轴上画出表示 的点吗?
活动探究
AB
1
2
BC
1
2
结合上面表格内容,尝试在数轴上画出 的点,你会选择哪组数据呢?
A
C
B
在直角三角形ABC中,若AC边为 则两条边AB和BC可以为多长?
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
你能在数轴上画出表示 的点吗?
思考:
0
1
2
3
4
l
A
B
C
你能在数轴上画出表示 的点和 的点吗?
√
√
0
1
2
3
4
A
B
C
课堂小结
怎样在数轴上表示无理数?
思想:以无理数为边构建直角三角形
(1)构造直角三角形
(2)在数轴上构造直角三角形。
(3)画弧
在数学中也有这样一幅美丽的“海螺型”图案
由此可知,利用勾股定理,可以作出长为
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
数学海螺图:
你能在数轴上表示出
的点吗?
的线段.
1.判断正误:
(1)所有的无理数都能在数轴上表示.( )
(2)数轴上的点都表示无理数.( )
√
×
自我检测1:
一、完成下列题目:
1、
①若两条直角边分别为1和1,则斜边的长为 ;
②若两条直角边分别为 2和1,则斜边的长为 ;
③若两条直角边分别为 3和1,则斜边的长为 ;
④若两条直角边分别为 4和1,则斜边的长为 ;
⑤若两条直角边分别为 5和1,则斜边的长为 ;
⑥若两条直角边分别为 6和1,则斜边的为 ;
……
?
1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段?
A
练习&1
?
2.如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个?写出落在x轴上的顶点坐标.
O
D
⌒
C
E
F
H
x
y
练习&1
?
17.1 勾股定理
第3课时
2、能在数轴上标出 、 、 等无理数。
1、理解勾股定理并能对无理数 : 、 、 、
、 等作出几何解释。
3、通过作图体会数形结合的思想。
重点:在数轴上标出无理数的点。
难点:理解尺规作图的原理。
1.已知直角三角形ABC的三边为a、b、c , ∠C= 90°,则 a、b、c 三者之间的关系是 ;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是 ;
3. 叫做无理数.
知识回顾
a2+b2=c2
无限不循环小数
问题思考
在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
B
A
C
C′
A′
B′
B
A
C
C′
A′
B′
已知两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°,? AB=A′B′,? BC=B′C′.
求证:△ABC≌△ A′B′C′ .
问题思考
证明:∵△ABC和 △A′B′C′是直角三角形,
∴AC?=AB?-BC?,
∴ A′C′ ?= A′B′ ?- B′C′ ?.
∵AB= A′B′ ,?BC= B′C′ ,
∴AC?= A′C′ ?,
∴AC= A′C′ .
在△ABC和△ A′B′C′中,
∵∠C=∠C′ , AC= A′C′ , BC= B′C′,
∴△ABC≌△ A′B′C′.
?????????
实数
数轴上的点
一一对应
说出下列数轴上各字母所表示的实数:
A B C D
-2 -1 0 1 2
点C表示
点D表示
点B表示
点A表示
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?
-1 0 1 2 3
你能在数轴上表示出 的点吗?
你能在数轴上画出表示 的点吗?
思考:
√
√
探究二:你能在数轴上画出表示 的点吗?
活动探究
AB
1
2
BC
1
2
结合上面表格内容,尝试在数轴上画出 的点,你会选择哪组数据呢?
A
C
B
在直角三角形ABC中,若AC边为 则两条边AB和BC可以为多长?
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
你能在数轴上画出表示 的点吗?
思考:
0
1
2
3
4
l
A
B
C
你能在数轴上画出表示 的点和 的点吗?
√
√
0
1
2
3
4
A
B
C
课堂小结
怎样在数轴上表示无理数?
思想:以无理数为边构建直角三角形
(1)构造直角三角形
(2)在数轴上构造直角三角形。
(3)画弧
在数学中也有这样一幅美丽的“海螺型”图案
由此可知,利用勾股定理,可以作出长为
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
数学海螺图:
你能在数轴上表示出
的点吗?
的线段.
1.判断正误:
(1)所有的无理数都能在数轴上表示.( )
(2)数轴上的点都表示无理数.( )
√
×
自我检测1:
一、完成下列题目:
1、
①若两条直角边分别为1和1,则斜边的长为 ;
②若两条直角边分别为 2和1,则斜边的长为 ;
③若两条直角边分别为 3和1,则斜边的长为 ;
④若两条直角边分别为 4和1,则斜边的长为 ;
⑤若两条直角边分别为 5和1,则斜边的长为 ;
⑥若两条直角边分别为 6和1,则斜边的为 ;
……
?
1、如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段?
A
练习&1
?
2.如图,D(2,1),以OD为一边画等腰三角形,并且使另一个顶点在x轴上,这样的等腰三角形能画多少个?写出落在x轴上的顶点坐标.
O
D
⌒
C
E
F
H
x
y
练习&1
?
