直角三角形全等的判定

直角三角形全等的判定
课型：预展结合课 班级： 学习小组： 小组人姓名：
【 学习目标 】
1、已知斜边和直角边会作直角三角形； 2、熟练掌握“斜边、直角边公理”，以及熟练地利用这个公理和判定两个直角三角形全等； 3、熟练使用“分析综合法”探求解题思路。
1．说出判定一般三角形全等的依据，并说出它们的共同点。
2．判断：如图，具有下列条件的Rt△ABC与Rt△A′B′C′ （其中∠C＝∠C′＝90。）是否全等， 如果全等请在（　） 里填写理由；如果不全等，在（　）里打“×”：
（1）AC＝A′C′,∠A＝A′　　 （　 ）
（2）AC＝A′C′，BC＝B′C′　（ 　）
（3）∠A＝∠A′，∠B＝∠B′　（　 ）
（4）AC＝A′C′，AB＝A′B′　（　 ）
例1．如图，已知线段、（）。画一个Rt△ABC，使∠C＝90°，一直角边CB＝a，斜边AB＝c。
2、判定两个直角三角形全等的定理理： 。 简写为： 。
你能用几何语言描述一下两个直角三角形全等的定理吗？（写出证明两个直角三角形全等的条件）
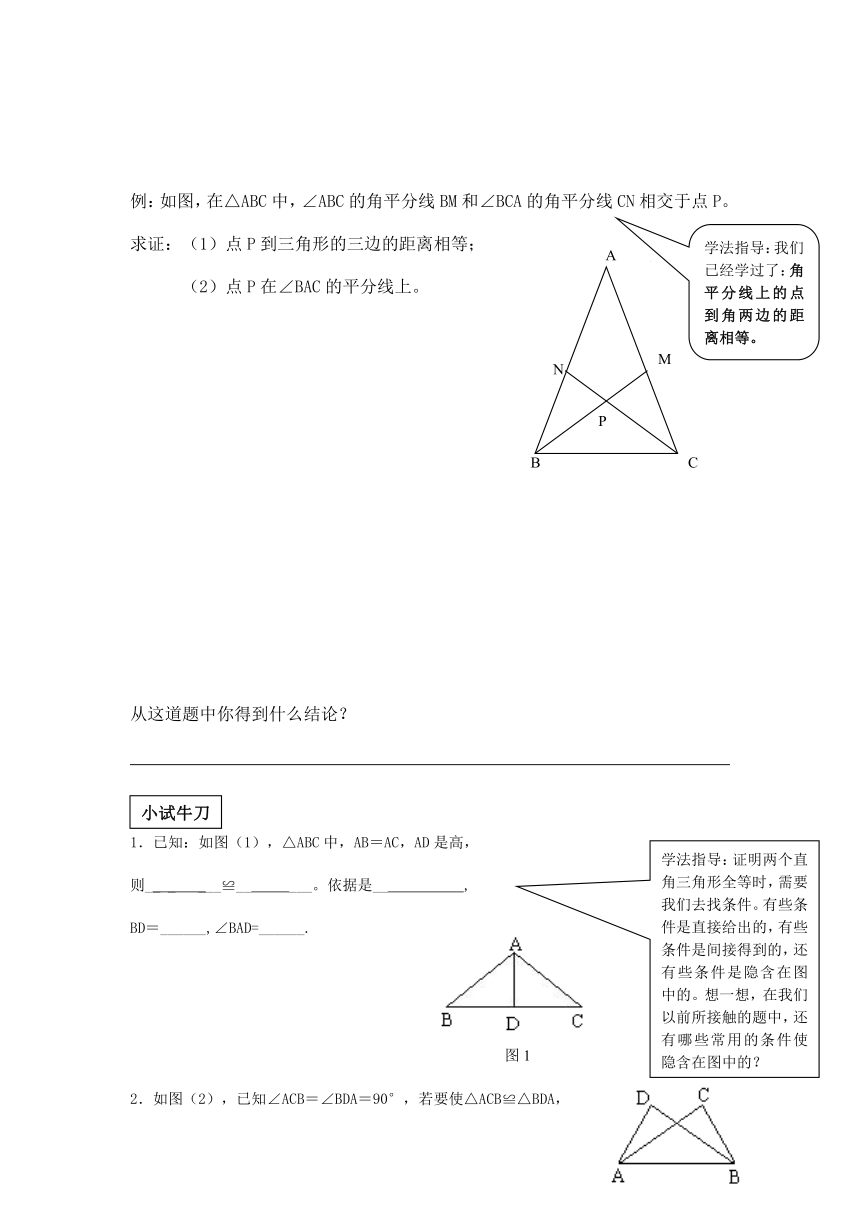
例：如图，在△ABC中，∠ABC的角平分线BM和∠BCA的角平分线CN相交于点P。
求证：（1）点P到三角形的三边的距离相等；
（2）点P在∠BAC的平分线上。
从这道题中你得到什么结论？
1．已知：如图（1），△ABC中，AB＝AC，AD是高，
则__ _ ___≌__ ___。依据是__ ,
BD＝______,∠BAD=______.
2．如图（2），已知∠ACB＝∠BDA＝90°，若要使△ACB≌△BDA，
还需要什么条件？把它们分别写出来。
1．“HL”公理是：有 相等的两个 三角形全等。
2．在应用“HL”公理时，必须先得出两个 三角形，然后证明 对应相等。
3．如图，AB＝AC，BD⊥AC于D，CE⊥AB于E，则图中全等的三角形对数为（　）
（A）1 　（B）2 　（C）3 　（D）4
这节课我能得 分，小组给我 分。
【家庭作业】（注意做题格式）
如图： AC⊥CB, BD⊥BC,AB=DC,求证：AB∥CD.
2．如图所示，已知∠1=∠2，∠ 3=∠4．求证：AB=AC．
思考题：
已知：如图，在△ABC和△A′B′C′中，CD、C′D′分别是高， 并且AC＝A′C′，CD＝C′D′，∠ACB＝∠A′C′B′。 求证：△ABC≌△A′B′C′
【预习作业】：
1、阅读教材P95-97
2、完成课后练习
3、剪4个全等的直角三角形。
检测你对旧知的掌握
测试你能成为数学家吗？
学法指导：再利用HL定理判断两个直角三角形全等时，我们需要注意什么？
学法指导：我们已经学过了：角平分线上的点到角两边的距离相等。
C
B
A
N
M
P
小试牛刀
学法指导：证明两个直角三角形全等时，需要我们去找条件。有些条件是直接给出的，有些条件是间接得到的，还有些条件是隐含在图中的。想一想，在我们以前所接触的题中，还有哪些常用的条件使隐含在图中的？
图1
图2
检测反馈
满分为十分