人教版数学八年下册 17.1 勾股定理第2课时课件(18张PPT)
文档属性
| 名称 | 人教版数学八年下册 17.1 勾股定理第2课时课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






文档简介
第十七章 勾股定理
17.1 勾股定理
第2课时
学习目标:
1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
3.经历探究勾股定理在实际问题中的应用过程,感受勾股定理的应用方法。
4.培养思维意识,发展数学理念,体会勾股定理的应用价值。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
回顾
什么是勾股定理?
探索
为什么叫勾股定理?
勾股定理是如何发现、证明、应用的?
勾股定理
What →
Why →
How →
What---勾股定理
直角三角形中,两条直角边a、b的平方和等于斜边c的平方。
a
b
c
如图,a?+b?=c?
即c =
结论变形
c2 = a2 + b2
a
b
c
A
B
C
运用勾股定理时应注意:
(1)找到直角三角形;
(2)认准直角边和斜边;
(3)两直角边的平方和等于斜边的平方。
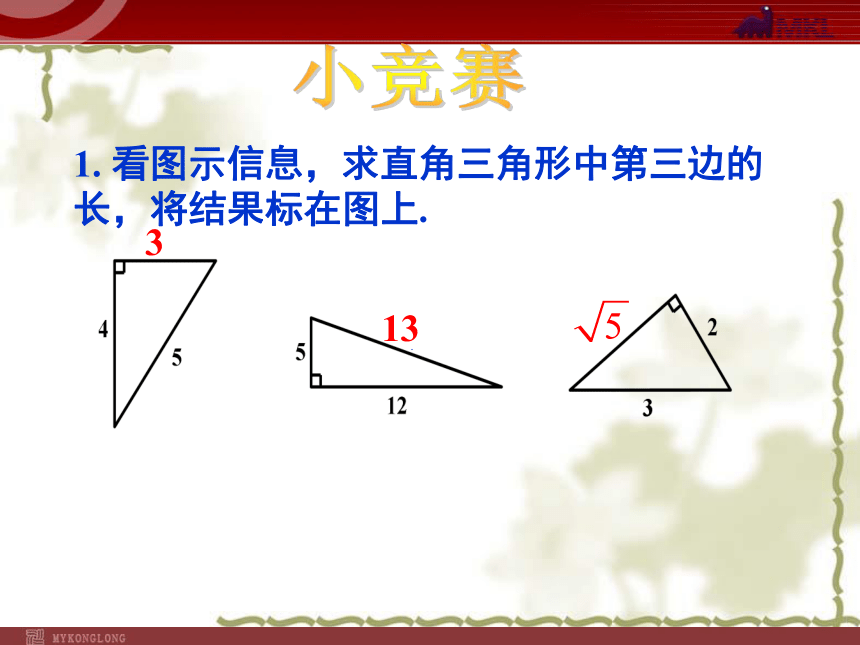
1. 看图示信息,求直角三角形中第三边的长,将结果标在图上.
3
.
13
.
2.(1)如图,两个正方形的面积分别是
S1=18,S2=12,则直角三角形的较短的直角边长
是 .
2.(2)如图,两个半圆的面积分别是S1=16π,S2=25π,则直角三角形的较短的直角边长是 .
3. 已知Rt△ABC中,∠C=90°,
若a=1,c=3,则b= .
4. 已知Rt△ABC中,∠A=90°, ∠B=30°,
若a=4,则c= .
5. 已知Rt△ABC中,∠B=90°, ∠A=45°,
若b=7 ,则c= .
7
思考:通过问题的解决你能否发现已知两直角边求出第三边有什么方法?在解决问题时,每个直角三角形需知晓几个条件?直角三角形中哪条边最长?
归纳:直角三角形中斜边最长,在解决问题时,每个直角三角形需知晓两个条件就可以求第三个量。
预习导航 知识再现:
有一种特殊的直角三角形,已知一边可以求另外两边长
A
C
B
b
a
c
45°
A
C
B
b
a
c
30°
a:b:c=1:1:√2
a:b:c=1:√3:2
a= 5 cm时求b=?c=?
c= 6 cm时求b=?a=?
例1:一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0。4m吗?
D
E
解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.52
∴BC=0.7m
由题意得:DE=AB=2.5m
DC=AC-AD=2.4-0.4=2m
在Rt△DCE中,
∴BE=1.5-0.7=0.8m≠0.4m
答;梯子底端B不是外移0.4m
∵∠DCE=90° ∴ DC2+ CE2=DE2
22+ BC2=2.52 ∴CE=1.5m
(2)一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
A
B
C
1 m
2 m
∵木板的宽2.2米大于1米,
∴ 横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.
∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?
(3)有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,
∴由勾股定理可知:
1. 一木杆在离地面3 m处折断,木杆顶端落在离木杆底端4 m处. 木杆折断之前有多高?
2. 一个圆锥的高AO=2.4 ,底面半径OB=0.7 . AB的长是多少?
练习
答案:8 m
答案:2.5
第1题图
第2题图
例2 在△ABC中,AB=15 cm,
AC=13 cm,高AD=12 cm,求BC的长.
高在BC边上 高在BC延长线上
答案:14 cm或4 cm.
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
17.1 勾股定理
第2课时
学习目标:
1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
3.经历探究勾股定理在实际问题中的应用过程,感受勾股定理的应用方法。
4.培养思维意识,发展数学理念,体会勾股定理的应用价值。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
回顾
什么是勾股定理?
探索
为什么叫勾股定理?
勾股定理是如何发现、证明、应用的?
勾股定理
What →
Why →
How →
What---勾股定理
直角三角形中,两条直角边a、b的平方和等于斜边c的平方。
a
b
c
如图,a?+b?=c?
即c =
结论变形
c2 = a2 + b2
a
b
c
A
B
C
运用勾股定理时应注意:
(1)找到直角三角形;
(2)认准直角边和斜边;
(3)两直角边的平方和等于斜边的平方。
1. 看图示信息,求直角三角形中第三边的长,将结果标在图上.
3
.
13
.
2.(1)如图,两个正方形的面积分别是
S1=18,S2=12,则直角三角形的较短的直角边长
是 .
2.(2)如图,两个半圆的面积分别是S1=16π,S2=25π,则直角三角形的较短的直角边长是 .
3. 已知Rt△ABC中,∠C=90°,
若a=1,c=3,则b= .
4. 已知Rt△ABC中,∠A=90°, ∠B=30°,
若a=4,则c= .
5. 已知Rt△ABC中,∠B=90°, ∠A=45°,
若b=7 ,则c= .
7
思考:通过问题的解决你能否发现已知两直角边求出第三边有什么方法?在解决问题时,每个直角三角形需知晓几个条件?直角三角形中哪条边最长?
归纳:直角三角形中斜边最长,在解决问题时,每个直角三角形需知晓两个条件就可以求第三个量。
预习导航 知识再现:
有一种特殊的直角三角形,已知一边可以求另外两边长
A
C
B
b
a
c
45°
A
C
B
b
a
c
30°
a:b:c=1:1:√2
a:b:c=1:√3:2
a= 5 cm时求b=?c=?
c= 6 cm时求b=?a=?
例1:一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0。4m吗?
D
E
解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.52
∴BC=0.7m
由题意得:DE=AB=2.5m
DC=AC-AD=2.4-0.4=2m
在Rt△DCE中,
∴BE=1.5-0.7=0.8m≠0.4m
答;梯子底端B不是外移0.4m
∵∠DCE=90° ∴ DC2+ CE2=DE2
22+ BC2=2.52 ∴CE=1.5m
(2)一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
A
B
C
1 m
2 m
∵木板的宽2.2米大于1米,
∴ 横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.
∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?
(3)有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,
∴由勾股定理可知:
1. 一木杆在离地面3 m处折断,木杆顶端落在离木杆底端4 m处. 木杆折断之前有多高?
2. 一个圆锥的高AO=2.4 ,底面半径OB=0.7 . AB的长是多少?
练习
答案:8 m
答案:2.5
第1题图
第2题图
例2 在△ABC中,AB=15 cm,
AC=13 cm,高AD=12 cm,求BC的长.
高在BC边上 高在BC延长线上
答案:14 cm或4 cm.
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
