人教版数学八年下册 17.2 勾股定理最短路径问题(17张PPT)
文档属性
| 名称 | 人教版数学八年下册 17.2 勾股定理最短路径问题(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:11:37 | ||
图片预览


文档简介
难点名称:利用勾股定理解决立体图形表面上最短路线问题
*
八年级-下册-第十七章
课题:《勾股定理》
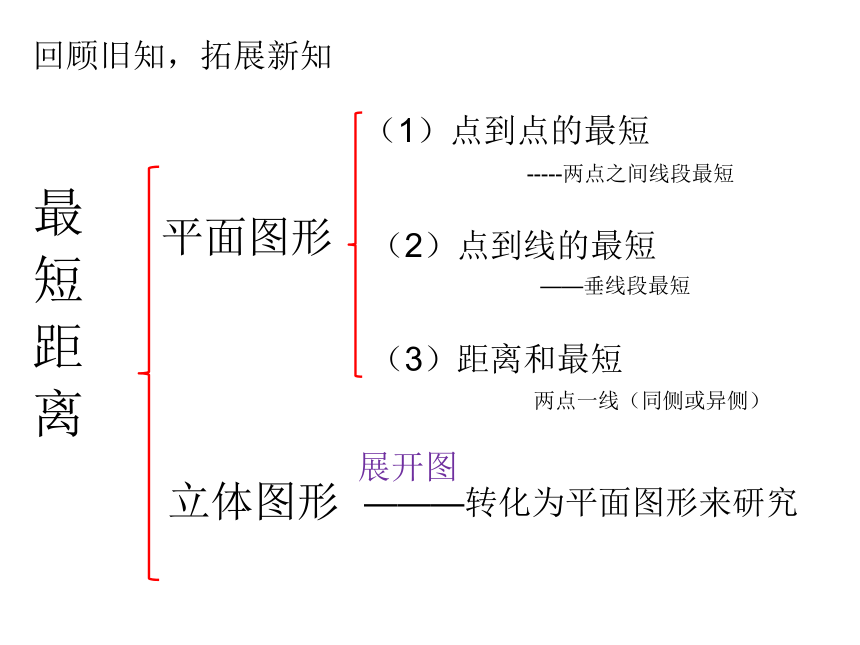
回顾旧知,拓展新知
最 短 距 离
平面图形
立体图形
(1)点到点的最短
(2)点到线的最短
(3)距离和最短
-----两点之间线段最短
——垂线段最短
两点一线(同侧或异侧)
———转化为平面图形来研究
展开图
导入
*
我该选择哪条路呢?
两点之间,线段最短。
有一个长方形花圃,有人避开拐角在花园内走出了一条小路.问:这么走的理论依据是什么?他们仅仅少走了多少步? (假设2步为1米)
(2)少走了(7-5 )x2=4步
(1)理论依据:
两点之间线段最短
导入
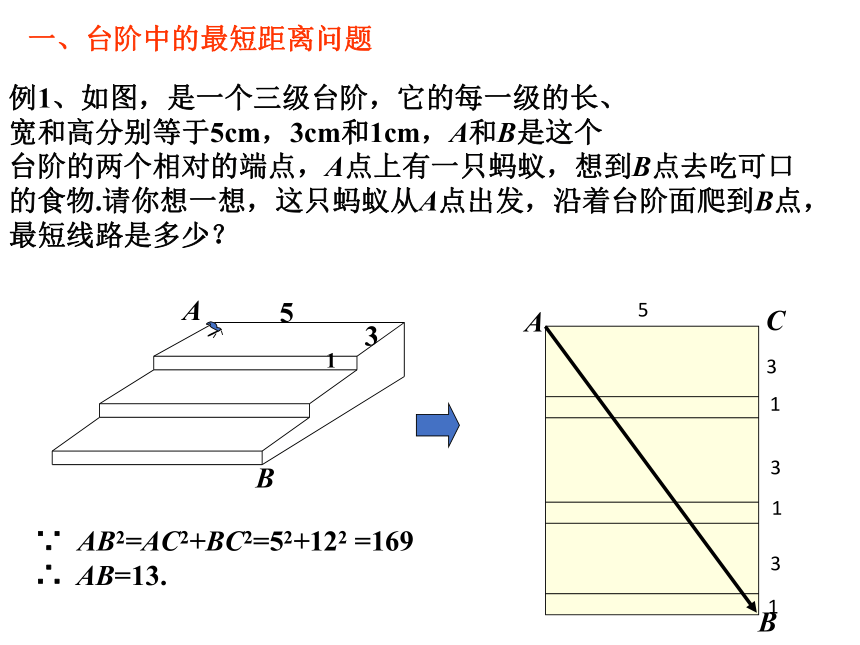
例1、如图,是一个三级台阶,它的每一级的长、
宽和高分别等于5cm,3cm和1cm,A和B是这个
台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
5
3
1
一、台阶中的最短距离问题
A
B
C
3
1
1
3
3
1
5
∵ AB2=AC2+BC2=52+122 =169
∴ AB=13.
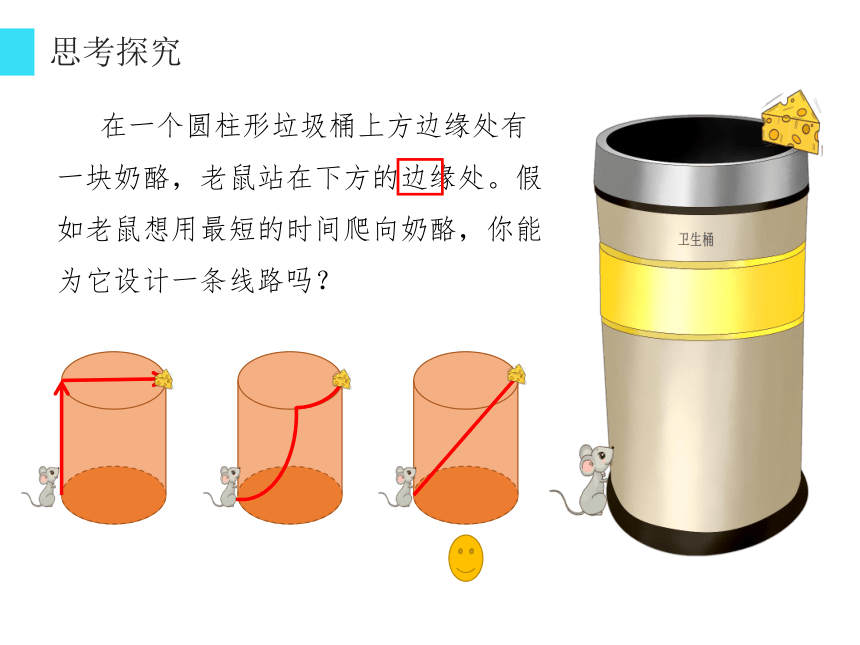
思考探究
在一个圆柱形垃圾桶上方边缘处有一块奶酪,老鼠站在下方的边缘处。假如老鼠想用最短的时间爬向奶酪,你能为它设计一条线路吗?
典例解析
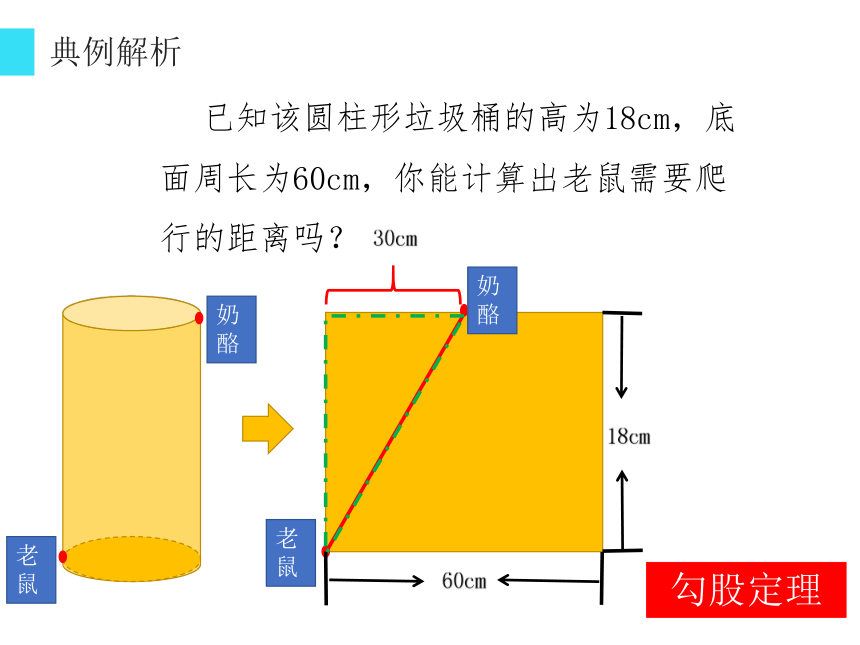
已知该圆柱形垃圾桶的高为18cm,底面周长为60cm,你能计算出老鼠需要爬行的距离吗?
奶酪
老鼠
奶酪
老鼠
勾股定理
归纳总结
立体图形
转化
展开
平面图形
勾股定理
a2+b2=c2
知识拓展
老鼠发现在棱长为8dm的魔方茶几上有一块草莓蛋糕(位置如图所示),你能帮助老鼠在最短的时间内吃到草莓蛋糕吗?
有多少种方法?是不是最短距离?
典例解析
AC2+CM2=AM2
82+162=AM2
AM= =
例题变形
已知长方体音响的长为3dm,宽为4dm,高为7dm。老鼠想要喝到长方体音响上的牛奶,你能帮它设计路线吗?最短的路线距离是多少?
有多少种方法?距离是否相等呢?
合作探究
NM2+CN2=CM2
32+112=CM2
CM= =
CM2+NM2=CN2
102+42=CN2
CN= =
合作探究
CM2+NM2=CN2
72+72=CN2
CN= =
最短路线距离
合作探究
NM2+CN2=CM2
32+112=CM2
CM= =
CM2+NM2=CN2
102+42=CN2
CN= =
合作探究
CM2+NM2=CN2
72+72=CN2
CN= =
最短路线距离
巩固练习
*
长方体的底面边长分别为3cm、1cm,高为6cm。如果从点C开始,经过4个侧面缠绕n圈后到达点A,那么所用细线最短需要________________cm.
n圈?
高:6cm
长:8n
【课堂小结】
立体图形中两点之间的最短距离
圆柱体
正方体
长方体
展开几何表面
化空间为平面
*
八年级-下册-第十七章
课题:《勾股定理》
回顾旧知,拓展新知
最 短 距 离
平面图形
立体图形
(1)点到点的最短
(2)点到线的最短
(3)距离和最短
-----两点之间线段最短
——垂线段最短
两点一线(同侧或异侧)
———转化为平面图形来研究
展开图
导入
*
我该选择哪条路呢?
两点之间,线段最短。
有一个长方形花圃,有人避开拐角在花园内走出了一条小路.问:这么走的理论依据是什么?他们仅仅少走了多少步? (假设2步为1米)
(2)少走了(7-5 )x2=4步
(1)理论依据:
两点之间线段最短
导入
例1、如图,是一个三级台阶,它的每一级的长、
宽和高分别等于5cm,3cm和1cm,A和B是这个
台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
5
3
1
一、台阶中的最短距离问题
A
B
C
3
1
1
3
3
1
5
∵ AB2=AC2+BC2=52+122 =169
∴ AB=13.
思考探究
在一个圆柱形垃圾桶上方边缘处有一块奶酪,老鼠站在下方的边缘处。假如老鼠想用最短的时间爬向奶酪,你能为它设计一条线路吗?
典例解析
已知该圆柱形垃圾桶的高为18cm,底面周长为60cm,你能计算出老鼠需要爬行的距离吗?
奶酪
老鼠
奶酪
老鼠
勾股定理
归纳总结
立体图形
转化
展开
平面图形
勾股定理
a2+b2=c2
知识拓展
老鼠发现在棱长为8dm的魔方茶几上有一块草莓蛋糕(位置如图所示),你能帮助老鼠在最短的时间内吃到草莓蛋糕吗?
有多少种方法?是不是最短距离?
典例解析
AC2+CM2=AM2
82+162=AM2
AM= =
例题变形
已知长方体音响的长为3dm,宽为4dm,高为7dm。老鼠想要喝到长方体音响上的牛奶,你能帮它设计路线吗?最短的路线距离是多少?
有多少种方法?距离是否相等呢?
合作探究
NM2+CN2=CM2
32+112=CM2
CM= =
CM2+NM2=CN2
102+42=CN2
CN= =
合作探究
CM2+NM2=CN2
72+72=CN2
CN= =
最短路线距离
合作探究
NM2+CN2=CM2
32+112=CM2
CM= =
CM2+NM2=CN2
102+42=CN2
CN= =
合作探究
CM2+NM2=CN2
72+72=CN2
CN= =
最短路线距离
巩固练习
*
长方体的底面边长分别为3cm、1cm,高为6cm。如果从点C开始,经过4个侧面缠绕n圈后到达点A,那么所用细线最短需要________________cm.
n圈?
高:6cm
长:8n
【课堂小结】
立体图形中两点之间的最短距离
圆柱体
正方体
长方体
展开几何表面
化空间为平面
