人教版八年级数学下册第18章 平行四边形 18.1.1平行四边形的性质 第1课时 平行四边形的边、角的特征课件 (共33张PPT)
文档属性
| 名称 | 人教版八年级数学下册第18章 平行四边形 18.1.1平行四边形的性质 第1课时 平行四边形的边、角的特征课件 (共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:12:03 | ||
图片预览






文档简介
18.1.1 平行四边形的性质
第十八章 平行四边形
第1课时 平行四边形的边、角特征
学习目标
1.理解并掌握平行四边形的概念及掌握平行四边形的定
义和对边相等、对角相等的两条性质.(重点)
2.根据平行四边形的性质进行简单的计算和证明.(难点)
3.经历“实验—猜想—验证—证明”的过程,发展学生的
思维水平.
观察下列图案,想一想它们都是什么形状?
有何特点?
新课导入
你还能举出其他的例子吗?
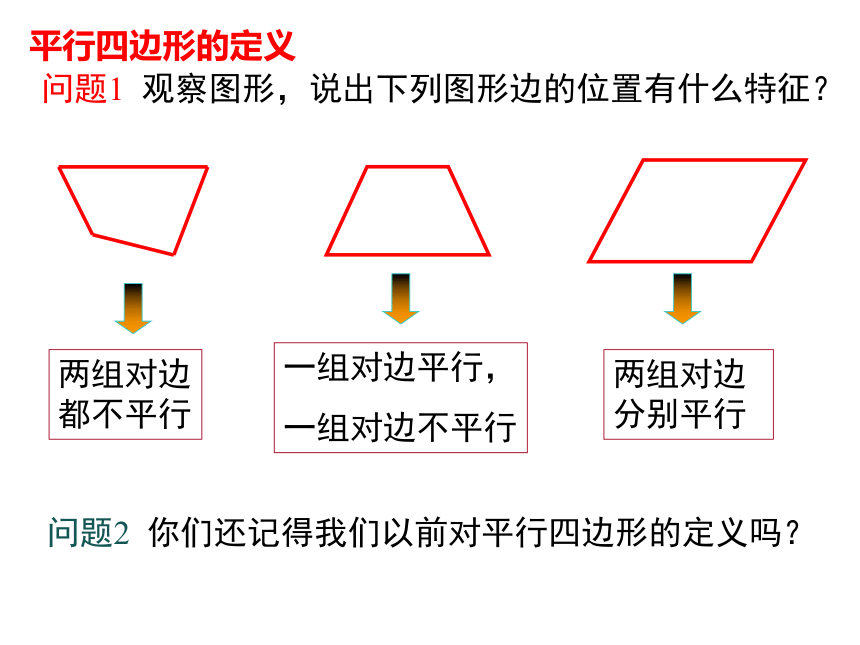
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 你们还记得我们以前对平行四边形的定义吗?
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示,如图,平行四边形ABCD
记作 ABCD ( 要注意字母顺序).
1.定义:
A
B
D
C
归纳总结
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
例1 如图,DC∥GH ∥ AB,DA∥ EF∥ CB,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
典例精析
解:∵DC∥GH ∥ AB,
DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有9个平行四边形,即
AEKG, ABHG, AEFD, GKFD,
K
BEKH, CHKF, BEFC, CDGH, ABCD.
用定义判定平行四边形,即看四边形两组对边是否分别平行.
归纳
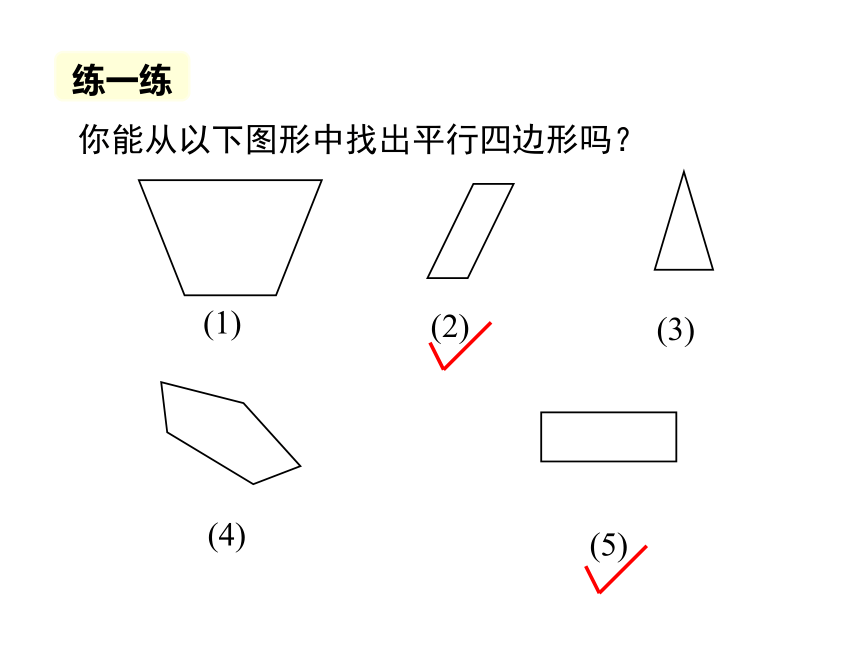
你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
练一练
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
平行四边形的边、角的特征
A
B
C
D
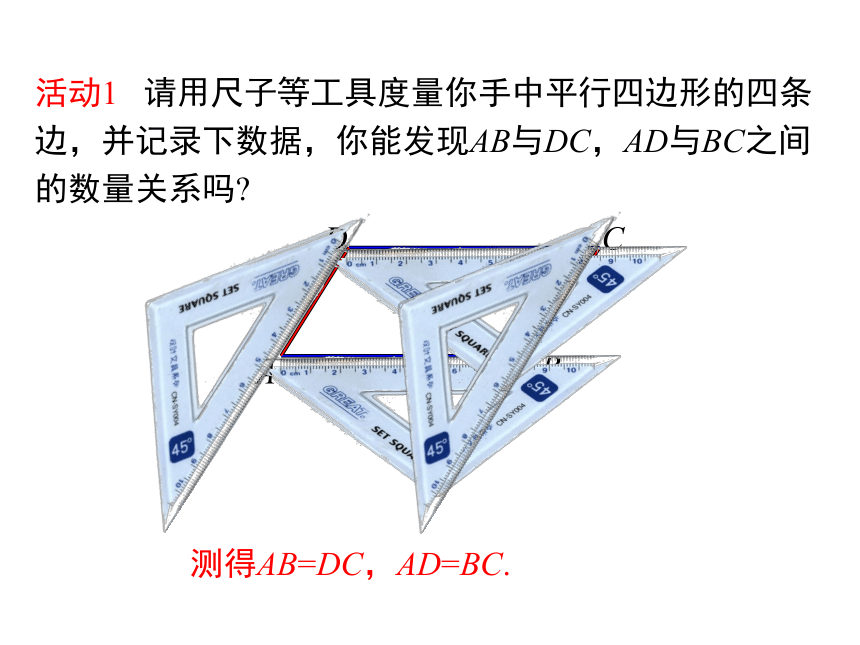
活动1 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗?
测得AB=DC,AD=BC.
A
B
C
D
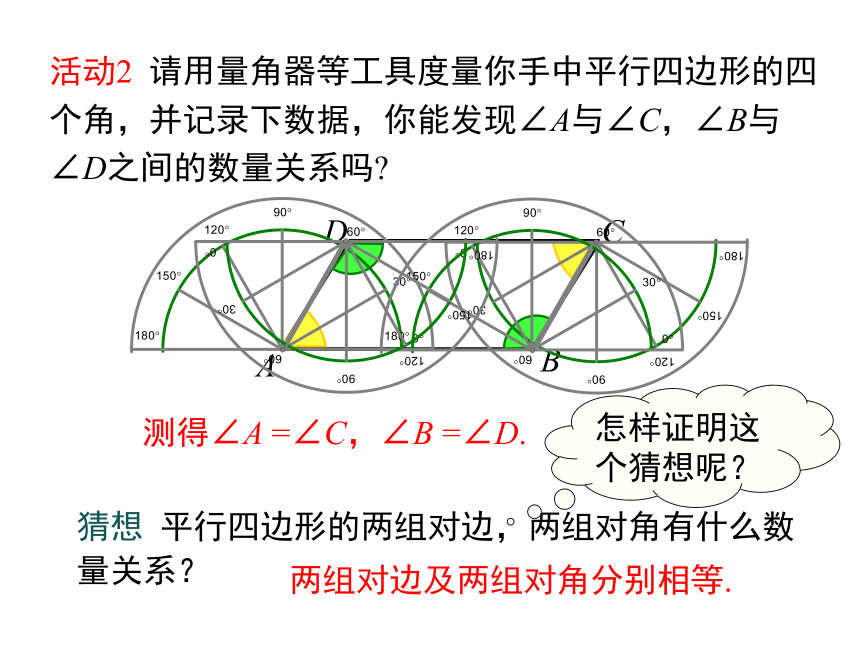
测得∠A =∠C,∠B =∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与 ∠D之间的数量关系吗?
猜想 平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.
怎样证明这个猜想呢?
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
证一证
思考 不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质除了对边互相平行以外,还有:
A
B
C
D
归纳总结
动手做一做:剪两张对边平行的纸条随意交叉叠放在一起,重合部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
A
B
C
D
解:AD和BC的长度相等.
理由如下:由题意知AB//CD,AD//BC,
∴四边形ABCD是平行四边形,
∴AD=BC.
例2 如图,在 ABCD中.
(1)若∠A =32。,求其余三个角的度数.
A
B
C
D
∵四边形ABCD是平行四边形,
解:
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
典例精析
(2)连接AC,已知 ABCD的周长等于20cm,AC=
7cm,求△ABC的周长.
解:∵四边形ABCD是平行四边形(已知),
∴AB=CD,BC=AD(平行四边形的对边相等).
又∵AB+BC+CD+AD=20cm(已知),
∴AB+BC= 10cm.
∵AC=7cm,
∴ △ABC的周长为AB+BC+AC= 17cm.
A
B
C
D
【变式题】 (1)在 ABCD中,∠A:∠B=2:3,求各角的度数.
解:∵∠A,∠B是平行四边形的两个邻角,
∴∠A+∠B=180°.
又∵∠A:∠B=2:3,
设∠A=2x,∠B=3x,
∴2x+3x= 180°,
解得x= 36°.
∴ ∠A = ∠C=72°, ∠B= ∠D=108°.
平行四边形的邻角互补
(2)若 ABCD的周长为28cm,AB:BC=3:4,求各边的长度.
解:在平行四边形ABCD中,
∵AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,
∴AB+BC= 14cm.
∵AB:BC=3:4,设AB=3ycm,BC=4ycm,
∴3y+4y=14,解得y=2.
∴AB=CD=6cm,BC=AD=8cm.
已知平行四边形的边角的比例关系求其他边角时,常会用到方程思想,结合平行四边形的性质列方程.
归纳
证明:∵四边形ABCD是平行四边形,
例3 如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AB ∥ CD
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
1.如图,在□ABCD中.
(1)若∠A=130°,则∠B=______ ,∠C=______ ,
∠D=______.
(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
(2)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
练一练
16
2.如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
平行线间的距离
例4 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS),
∴AE=CF.
思考 在上述证明中还能得出什么结论?
D
A
B
C
F
E
DE=BF
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A、C、E,交 n于B、D、F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
归纳总结
若m // n,AB、CD、EF垂直于 n,交n于B、D、F,交 m于A、C、E.
B
F
E
A
n
m
C
D
点到直线的距离
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC
=12cm2,求△ABD中AB边上的高.
解:S△ABC = AB?BC,
= ×4 ×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
练一练
当堂跟踪练习
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55° C. 65° D. 75°
A
A
B
C
M
D
2.判断题(对的在括号内填“√”,错的填“×”):
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°. ( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,
△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
3.如图,D、 E、F 分别在△ABC的边AB、BC、AC上,且DE∥AC,DF∥BC,EF∥AB,则图中有_____个平行
四边形.
第3题图
第4题图
3
证明: ∵四边形ABCD是平行四边形,
∴ AB∥CD,AD=BC.
∴ ∠CDE= ∠DEA,∠CFB= ∠FBA.
又∵DE,BF分别平分
∠ADC,∠ABC,
∴∠CDE= ∠ADE,∠CBF= ∠FBA,
∴ ∠DEA= ∠ADE,∠CFB=∠CBF,
∴AE=AD, CF=BC,
∴AE= CF.
5.已知在平行四边形ABCD中,DE平分∠ADC,BF平分∠ABC.求证:AE=CF.
A
B
D
C
E
F
6.有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°,且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=80cm.
∴ED=AD-AE=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
证明: ∵ 四边形BEFM是平行四边形,
∴BM=EF,AB//EF.
∵ AD平分∠BAC,
∴∠BAD=∠CAD.
∵AB//EF,
∴ ∠BAD=∠AEF,
∴∠CAD =∠AEF,
∴ AF=EF,
∴ AF=BM.
7.如图,在?ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM.
B
D
C
E
F
A
M
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的平行线段相等
两条平行线间的距离
两组对角分别相等,邻角互补
第十八章 平行四边形
第1课时 平行四边形的边、角特征
学习目标
1.理解并掌握平行四边形的概念及掌握平行四边形的定
义和对边相等、对角相等的两条性质.(重点)
2.根据平行四边形的性质进行简单的计算和证明.(难点)
3.经历“实验—猜想—验证—证明”的过程,发展学生的
思维水平.
观察下列图案,想一想它们都是什么形状?
有何特点?
新课导入
你还能举出其他的例子吗?
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 你们还记得我们以前对平行四边形的定义吗?
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示,如图,平行四边形ABCD
记作 ABCD ( 要注意字母顺序).
1.定义:
A
B
D
C
归纳总结
语言表述:
∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
例1 如图,DC∥GH ∥ AB,DA∥ EF∥ CB,图中的
平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
典例精析
解:∵DC∥GH ∥ AB,
DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有9个平行四边形,即
AEKG, ABHG, AEFD, GKFD,
K
BEKH, CHKF, BEFC, CDGH, ABCD.
用定义判定平行四边形,即看四边形两组对边是否分别平行.
归纳
你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
练一练
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
平行四边形的边、角的特征
A
B
C
D
活动1 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗?
测得AB=DC,AD=BC.
A
B
C
D
测得∠A =∠C,∠B =∠D.
活动2 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与 ∠D之间的数量关系吗?
猜想 平行四边形的两组对边,两组对角有什么数量关系?
两组对边及两组对角分别相等.
怎样证明这个猜想呢?
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
证一证
思考 不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质除了对边互相平行以外,还有:
A
B
C
D
归纳总结
动手做一做:剪两张对边平行的纸条随意交叉叠放在一起,重合部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
A
B
C
D
解:AD和BC的长度相等.
理由如下:由题意知AB//CD,AD//BC,
∴四边形ABCD是平行四边形,
∴AD=BC.
例2 如图,在 ABCD中.
(1)若∠A =32。,求其余三个角的度数.
A
B
C
D
∵四边形ABCD是平行四边形,
解:
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
典例精析
(2)连接AC,已知 ABCD的周长等于20cm,AC=
7cm,求△ABC的周长.
解:∵四边形ABCD是平行四边形(已知),
∴AB=CD,BC=AD(平行四边形的对边相等).
又∵AB+BC+CD+AD=20cm(已知),
∴AB+BC= 10cm.
∵AC=7cm,
∴ △ABC的周长为AB+BC+AC= 17cm.
A
B
C
D
【变式题】 (1)在 ABCD中,∠A:∠B=2:3,求各角的度数.
解:∵∠A,∠B是平行四边形的两个邻角,
∴∠A+∠B=180°.
又∵∠A:∠B=2:3,
设∠A=2x,∠B=3x,
∴2x+3x= 180°,
解得x= 36°.
∴ ∠A = ∠C=72°, ∠B= ∠D=108°.
平行四边形的邻角互补
(2)若 ABCD的周长为28cm,AB:BC=3:4,求各边的长度.
解:在平行四边形ABCD中,
∵AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,
∴AB+BC= 14cm.
∵AB:BC=3:4,设AB=3ycm,BC=4ycm,
∴3y+4y=14,解得y=2.
∴AB=CD=6cm,BC=AD=8cm.
已知平行四边形的边角的比例关系求其他边角时,常会用到方程思想,结合平行四边形的性质列方程.
归纳
证明:∵四边形ABCD是平行四边形,
例3 如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AB ∥ CD
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
1.如图,在□ABCD中.
(1)若∠A=130°,则∠B=______ ,∠C=______ ,
∠D=______.
(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
(2)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
练一练
16
2.如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
平行线间的距离
例4 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS),
∴AE=CF.
思考 在上述证明中还能得出什么结论?
D
A
B
C
F
E
DE=BF
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A、C、E,交 n于B、D、F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
归纳总结
若m // n,AB、CD、EF垂直于 n,交n于B、D、F,交 m于A、C、E.
B
F
E
A
n
m
C
D
点到直线的距离
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC
=12cm2,求△ABD中AB边上的高.
解:S△ABC = AB?BC,
= ×4 ×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
练一练
当堂跟踪练习
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55° C. 65° D. 75°
A
A
B
C
M
D
2.判断题(对的在括号内填“√”,错的填“×”):
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°. ( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,
△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
3.如图,D、 E、F 分别在△ABC的边AB、BC、AC上,且DE∥AC,DF∥BC,EF∥AB,则图中有_____个平行
四边形.
第3题图
第4题图
3
证明: ∵四边形ABCD是平行四边形,
∴ AB∥CD,AD=BC.
∴ ∠CDE= ∠DEA,∠CFB= ∠FBA.
又∵DE,BF分别平分
∠ADC,∠ABC,
∴∠CDE= ∠ADE,∠CBF= ∠FBA,
∴ ∠DEA= ∠ADE,∠CFB=∠CBF,
∴AE=AD, CF=BC,
∴AE= CF.
5.已知在平行四边形ABCD中,DE平分∠ADC,BF平分∠ABC.求证:AE=CF.
A
B
D
C
E
F
6.有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°,且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=80cm.
∴ED=AD-AE=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
证明: ∵ 四边形BEFM是平行四边形,
∴BM=EF,AB//EF.
∵ AD平分∠BAC,
∴∠BAD=∠CAD.
∵AB//EF,
∴ ∠BAD=∠AEF,
∴∠CAD =∠AEF,
∴ AF=EF,
∴ AF=BM.
7.如图,在?ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM.
B
D
C
E
F
A
M
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等
两条平行线间的平行线段相等
两条平行线间的距离
两组对角分别相等,邻角互补
