初中数学人教版八年级下册第十九章 2 专题复习:一次函数图象与性质(2)课件(共28张PPT)
文档属性
| 名称 | 初中数学人教版八年级下册第十九章 2 专题复习:一次函数图象与性质(2)课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 309.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:17:05 | ||
图片预览








文档简介
人教版初中数学八年级下册
一次函数的图象与性质(2)
复习
1.进一步掌握用待定系数法求一次函数解析式的方法步骤。(重点)
2.培养学生从问题中分析确定求一次函数解析式条件的能力。(难点)
3.体会分类、转化、数形结合、方程等数学思想方法,感受数学的应用价值.
用待定系数法求一次函数解析式
核心素养
2.用待定系数法求一次函数解析式的一般步骤:
一设:设出一次函数解析式的一般形式y=kx+b ;
二列:把已知点的坐标代入y=kx+b,
列出关于k、b的二元一次方程组;
三解:解这个方程组,求出k、b的值;
四写:把求得的k、b的值代入y=kx+b,写出函数解析式.
一.基础知识
1.一次函数的一般形式: y=kx+b(k≠0)
解:设这个一次函数的解析式为y=kx+b,
把(3,5)与(-4,-9)代入 y=kx+b,得
∴这个一次函数的解析式为y=2x-1.
例1.已知一次函数的图象经过点(3,5)与
(-4,-9),求这个一次函数的解析式.
3k+b=5
-4k+b=-9
解得,
k=2
b=-1
一设
二列
三解
四写
二、考点解析:
考点一:利用已知点的坐标求解析式
已知一个一次函数,当自变量x=-2时,函数值y=-1,当x=3时,y=-3.求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b,
由已知条件x=-2时,y=-1, x=3时,y=-3,得
解,得
∴一次函数的解析式为y=- x- .
跟踪练习一:
例2.已知正比例函数y=2x与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),求一次函数的解析式.
考点二:利用图象求解析式
解:把点A(m,2)代入y=2x,可得2=2m,
∴ A点坐标为(1,2),
∴
∴这个一次函数的解析式为y=x+1.
k+b=2
-2k+b=-1
解得,
k=1
b=1
解得m=1,
又∵一次函数还经过点B(-2,-1),
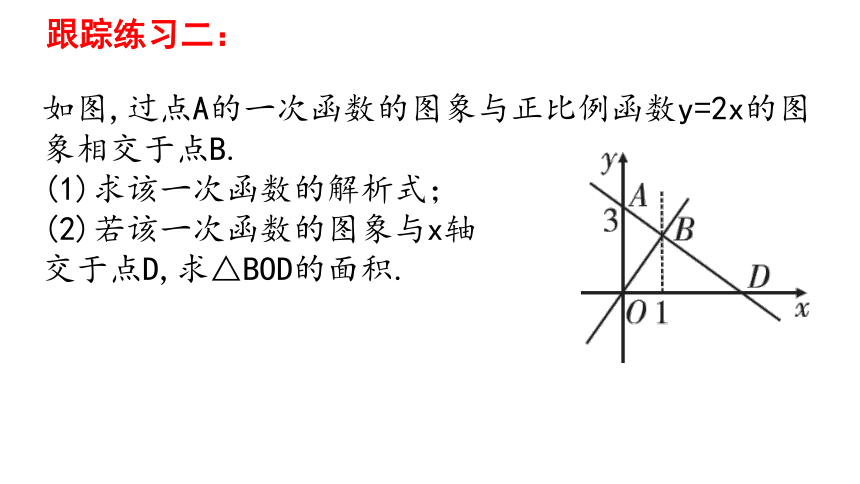
如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求该一次函数的解析式;
(2)若该一次函数的图象与x轴
交于点D,求△BOD的面积.
跟踪练习二:
解:(1)在y=2x中,当x=1时,得y=2,
则点B的坐标是(1,2).
设一次函数的解析式是y=kx+b,
∴一次函数的解析式是y=-x+3.
(2)一次函数的解析式y=-x+3中,
当y=0时,得x=3,
则点D的坐标是(3,0).
∴S△BOD= =3.
知识拓展
利用函数图象求一次函数解析式时,首先要将图形语言转化为符号语言,建立数学模型;其次要注意选择合适的点,并求出点的坐标,再利用待定系数法求出函数解析式。
A(3,0)
考点三:利用面积求解析式
例3.已知一次函数y=kx+b的图象过点A(3,0),与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式.
解:∵点A(3,0),
∴OA=3.
∵ S△AOB= OA?OB = ×3×OB=6,
?
?
∴OB=4,
∴B点坐标为(0,4)或(0,-4),
当B点坐标为(0,4)时,可得函数解析式为y= x+4;
?
当B点坐标为(0,-4)时,可解得函数解析式为y= x-4.
?
x
y
O
?
B
?
B
?
分类思想
知识拓展
利用一次函数图像与坐标轴围成的三角形面积求函数解析式, 题目中无函数图象时,紧扣“B”点的位置不确定(在y轴正半轴还是负半轴不确定)性,进行分类求解。
解:∵y=kx+b的图象与y=2x平行,
∴k=2,
∴这个一次函数的解析式为y=2x-5.
考点四:利用已知平行或平移求解析式
例4.已知直线y=kx+b的图象与y=2x平行且过点(2,-1),求这个一次函数的解析式.
解得b=-5,
∴y=2x+b,
∵y=2x+b的图象过点(2,-1),
∴-1=2×2+b,
直线y1=k1x+b1与直线y2=k2x+b2平行 k1=k2且b1≠b2
1.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb= .
解:∵y=kx+b的图象与正比例函数y=2x 的图象平行,
∴k=2,
∵y=kx+b的图象经过点A(1﹣2),
∴2+b=﹣2,
解,得b=﹣4,
∴kb=2×(﹣4)=﹣8.
跟踪练习三:
-8
变 式 题
2.把直线y=2x-1向上平移2个单位得到的图象解析式为_______.
∵直线y=2x-1向上平移2个单位,
解:设平移后的函数解析式为y=kx+b,
∵直线y=2x-1平移后的图象与y=2x-1平行,
∴k=2,
∴这个一次函数的解析式为y=2x+1.
解得b=1,
∴y=2x+b,
∴2x+b=2x-1+2,
x
y
O
y=2x+1
y=2x+1
y=2x-1
2.把直线y=2x-1向上平移2个单位得到的图象解析式为_______.
y=2x+1
一次函数图像的平移规律:
假如y=kx+b向左平移m个单位就是y=k(x+m)+b,
左加右减
(自变量变化)
假如y=kx+b向上平移m个单位就是y=kx+b+m,
上加下减
(常数项变化)
x
y
y=2x+1
y=2x-1
假如y=kx+b向下平移m个单位就是y=kx+b-m。
假如y=kx+b向右平移m个单位就是y=k(x-m)+b。
x
y
O
y=2x-1
假如y=kx+b向左平移m个单位就是y=k(x+m)+b,向右平移m个单位就是y=k(x-m)+b。
2、左加右减:
(自变量变化)
假如y=kx+b向上平移m个单位就是y=kx+b+m,向下平移m个单位就是y=kx+b-m。
1、上加下减:
(常数项变化)
(1)把直线y=2x-1向上平移1个单位
得到的图象解析式为__ _____.
(2)把直线y=2x-1向左平移1个单位
得到的图象解析式为___ ____.
(3)把直线y=2x-1向右平移1个单位
得到的图象解析式为__ ____.
y=2x-2
y=2x-3
y=2x+1
?
第一套
第二套
椅子的高x(cm)
40
37
桌子的高y(cm)
75
70.2
(1) 求出y与x之间的函数关系式.
(2) 现有一把高42cm 的椅子和一张高为78.2cm 的课桌,它们是否配套?通过计算说明.
三、能力提升:利用一次函数解决实际问题
例5.为了保护学生视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的高度:
分析:(1)由表中信息可知,当x=40时,y=75;当x=37时,y=70.2,因此可用待定系数法求出其函数解析式;(2)“是否配套”实际问题转化为数学问题就是问(42,78.2)这个点坐标是否满足(1)中的解析式.
解:(1)设y与x的函数关系式是y=kx+b.根据题意得
解得
40k+b=75
37k+b=70.2
k=1.6
b=11
∴y与x的函数关系式是y=1.6x+11.
(2)将x=42代入y=1.6x+11得
y=1.6×42+11=78.2
∴这套课桌椅是配套的.
小李从西安通过某快递公司给在南昌的外婆寄
一盒樱桃,快递时,他了解到这个公司除了收取
每次6元包装费外,樱桃不超过1 kg收费22元,超
过1 kg,则超出部分每千克加收10元费用,设该
公司从西安到南昌快寄樱桃的费用为y(元),所寄
樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5 kg樱桃,请你求出
这次快寄的费用是多少元?
跟踪练习四:
解:(1)当 时,y=28.
当x>1时,y是x的一次函数
设这个一次函数的解析式为y=kx+b,
把(1,28)与(3,48)代入 y=kx+b,得
O
48
28
1
3
y(元)
x(kg)
k+b=28
解得,
k=10
b=18
3k+b=48
(2)当x=2.5时,y=10×2.5+18=43.
所以小李这次快递的费用是43元。
∴ y =10x+8
知识拓展
确定实际问题中的一次函数关系式时,首先要将实际问题转化为数学问题,即建立数学模型;其次是建立函数与自变量的关系式,要注意确定自变量的取值范围.若题目中体现具有一次函数关系则用待定系数法求解析式,若题目中没有体现一次函数关系,则根据实际意义求函数关系式。
四、课后小结
五、基础过关
1.一次函数 y=kx+3 的图象经过点(-1,5),则
k=____
2.(陕西)根据下表中一次函数
的自变量 x 与 y 的对应值,
可得 P 的值为( )
1 B. -1 C. 3 D. -3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-2
0
1
y
3
p
0
3.已知一次函数的图象经过点A(2,-1)和点B,其中点B是另一条直线 y=- ━x+3 与y轴的交点,这个
一次函数的表达式 。
1
2
y=-2x+3
-2
A
4、某车油箱现有汽油50升,行驶时,油箱中的余油量
y(升)是行驶路程x(km)的一次函数,其图象如图
所示求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
解得
①
②
六、课后作业
必做:1.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式
2.若一次函数的图象与直线y=-3x+2交y轴于同一点,且过点(2,-6),求此函数解析式.
?
4.小明将父母给的零用钱按每月相等的数额存在储
蓄盒内,盒内钱数y(元)与存钱月数 x(月)之
间的关系如图所示.
(1)求y关于x的函数解析式;
(2)经过几个月小明才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
能力提升
(1)若直线y=kx+b与直线y=2x+1关于x轴对称,求k和b的值.
(2)若直线y=kx+b与直线y=2x+1关于y轴对称,求k和b的值.
由上面的结论,你能发现什么规律?
x
O
y
y=2x+1
一次函数的图象与性质(2)
复习
1.进一步掌握用待定系数法求一次函数解析式的方法步骤。(重点)
2.培养学生从问题中分析确定求一次函数解析式条件的能力。(难点)
3.体会分类、转化、数形结合、方程等数学思想方法,感受数学的应用价值.
用待定系数法求一次函数解析式
核心素养
2.用待定系数法求一次函数解析式的一般步骤:
一设:设出一次函数解析式的一般形式y=kx+b ;
二列:把已知点的坐标代入y=kx+b,
列出关于k、b的二元一次方程组;
三解:解这个方程组,求出k、b的值;
四写:把求得的k、b的值代入y=kx+b,写出函数解析式.
一.基础知识
1.一次函数的一般形式: y=kx+b(k≠0)
解:设这个一次函数的解析式为y=kx+b,
把(3,5)与(-4,-9)代入 y=kx+b,得
∴这个一次函数的解析式为y=2x-1.
例1.已知一次函数的图象经过点(3,5)与
(-4,-9),求这个一次函数的解析式.
3k+b=5
-4k+b=-9
解得,
k=2
b=-1
一设
二列
三解
四写
二、考点解析:
考点一:利用已知点的坐标求解析式
已知一个一次函数,当自变量x=-2时,函数值y=-1,当x=3时,y=-3.求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b,
由已知条件x=-2时,y=-1, x=3时,y=-3,得
解,得
∴一次函数的解析式为y=- x- .
跟踪练习一:
例2.已知正比例函数y=2x与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),求一次函数的解析式.
考点二:利用图象求解析式
解:把点A(m,2)代入y=2x,可得2=2m,
∴ A点坐标为(1,2),
∴
∴这个一次函数的解析式为y=x+1.
k+b=2
-2k+b=-1
解得,
k=1
b=1
解得m=1,
又∵一次函数还经过点B(-2,-1),
如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求该一次函数的解析式;
(2)若该一次函数的图象与x轴
交于点D,求△BOD的面积.
跟踪练习二:
解:(1)在y=2x中,当x=1时,得y=2,
则点B的坐标是(1,2).
设一次函数的解析式是y=kx+b,
∴一次函数的解析式是y=-x+3.
(2)一次函数的解析式y=-x+3中,
当y=0时,得x=3,
则点D的坐标是(3,0).
∴S△BOD= =3.
知识拓展
利用函数图象求一次函数解析式时,首先要将图形语言转化为符号语言,建立数学模型;其次要注意选择合适的点,并求出点的坐标,再利用待定系数法求出函数解析式。
A(3,0)
考点三:利用面积求解析式
例3.已知一次函数y=kx+b的图象过点A(3,0),与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式.
解:∵点A(3,0),
∴OA=3.
∵ S△AOB= OA?OB = ×3×OB=6,
?
?
∴OB=4,
∴B点坐标为(0,4)或(0,-4),
当B点坐标为(0,4)时,可得函数解析式为y= x+4;
?
当B点坐标为(0,-4)时,可解得函数解析式为y= x-4.
?
x
y
O
?
B
?
B
?
分类思想
知识拓展
利用一次函数图像与坐标轴围成的三角形面积求函数解析式, 题目中无函数图象时,紧扣“B”点的位置不确定(在y轴正半轴还是负半轴不确定)性,进行分类求解。
解:∵y=kx+b的图象与y=2x平行,
∴k=2,
∴这个一次函数的解析式为y=2x-5.
考点四:利用已知平行或平移求解析式
例4.已知直线y=kx+b的图象与y=2x平行且过点(2,-1),求这个一次函数的解析式.
解得b=-5,
∴y=2x+b,
∵y=2x+b的图象过点(2,-1),
∴-1=2×2+b,
直线y1=k1x+b1与直线y2=k2x+b2平行 k1=k2且b1≠b2
1.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb= .
解:∵y=kx+b的图象与正比例函数y=2x 的图象平行,
∴k=2,
∵y=kx+b的图象经过点A(1﹣2),
∴2+b=﹣2,
解,得b=﹣4,
∴kb=2×(﹣4)=﹣8.
跟踪练习三:
-8
变 式 题
2.把直线y=2x-1向上平移2个单位得到的图象解析式为_______.
∵直线y=2x-1向上平移2个单位,
解:设平移后的函数解析式为y=kx+b,
∵直线y=2x-1平移后的图象与y=2x-1平行,
∴k=2,
∴这个一次函数的解析式为y=2x+1.
解得b=1,
∴y=2x+b,
∴2x+b=2x-1+2,
x
y
O
y=2x+1
y=2x+1
y=2x-1
2.把直线y=2x-1向上平移2个单位得到的图象解析式为_______.
y=2x+1
一次函数图像的平移规律:
假如y=kx+b向左平移m个单位就是y=k(x+m)+b,
左加右减
(自变量变化)
假如y=kx+b向上平移m个单位就是y=kx+b+m,
上加下减
(常数项变化)
x
y
y=2x+1
y=2x-1
假如y=kx+b向下平移m个单位就是y=kx+b-m。
假如y=kx+b向右平移m个单位就是y=k(x-m)+b。
x
y
O
y=2x-1
假如y=kx+b向左平移m个单位就是y=k(x+m)+b,向右平移m个单位就是y=k(x-m)+b。
2、左加右减:
(自变量变化)
假如y=kx+b向上平移m个单位就是y=kx+b+m,向下平移m个单位就是y=kx+b-m。
1、上加下减:
(常数项变化)
(1)把直线y=2x-1向上平移1个单位
得到的图象解析式为__ _____.
(2)把直线y=2x-1向左平移1个单位
得到的图象解析式为___ ____.
(3)把直线y=2x-1向右平移1个单位
得到的图象解析式为__ ____.
y=2x-2
y=2x-3
y=2x+1
?
第一套
第二套
椅子的高x(cm)
40
37
桌子的高y(cm)
75
70.2
(1) 求出y与x之间的函数关系式.
(2) 现有一把高42cm 的椅子和一张高为78.2cm 的课桌,它们是否配套?通过计算说明.
三、能力提升:利用一次函数解决实际问题
例5.为了保护学生视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的高度:
分析:(1)由表中信息可知,当x=40时,y=75;当x=37时,y=70.2,因此可用待定系数法求出其函数解析式;(2)“是否配套”实际问题转化为数学问题就是问(42,78.2)这个点坐标是否满足(1)中的解析式.
解:(1)设y与x的函数关系式是y=kx+b.根据题意得
解得
40k+b=75
37k+b=70.2
k=1.6
b=11
∴y与x的函数关系式是y=1.6x+11.
(2)将x=42代入y=1.6x+11得
y=1.6×42+11=78.2
∴这套课桌椅是配套的.
小李从西安通过某快递公司给在南昌的外婆寄
一盒樱桃,快递时,他了解到这个公司除了收取
每次6元包装费外,樱桃不超过1 kg收费22元,超
过1 kg,则超出部分每千克加收10元费用,设该
公司从西安到南昌快寄樱桃的费用为y(元),所寄
樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5 kg樱桃,请你求出
这次快寄的费用是多少元?
跟踪练习四:
解:(1)当 时,y=28.
当x>1时,y是x的一次函数
设这个一次函数的解析式为y=kx+b,
把(1,28)与(3,48)代入 y=kx+b,得
O
48
28
1
3
y(元)
x(kg)
k+b=28
解得,
k=10
b=18
3k+b=48
(2)当x=2.5时,y=10×2.5+18=43.
所以小李这次快递的费用是43元。
∴ y =10x+8
知识拓展
确定实际问题中的一次函数关系式时,首先要将实际问题转化为数学问题,即建立数学模型;其次是建立函数与自变量的关系式,要注意确定自变量的取值范围.若题目中体现具有一次函数关系则用待定系数法求解析式,若题目中没有体现一次函数关系,则根据实际意义求函数关系式。
四、课后小结
五、基础过关
1.一次函数 y=kx+3 的图象经过点(-1,5),则
k=____
2.(陕西)根据下表中一次函数
的自变量 x 与 y 的对应值,
可得 P 的值为( )
1 B. -1 C. 3 D. -3
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-2
0
1
y
3
p
0
3.已知一次函数的图象经过点A(2,-1)和点B,其中点B是另一条直线 y=- ━x+3 与y轴的交点,这个
一次函数的表达式 。
1
2
y=-2x+3
-2
A
4、某车油箱现有汽油50升,行驶时,油箱中的余油量
y(升)是行驶路程x(km)的一次函数,其图象如图
所示求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
解得
①
②
六、课后作业
必做:1.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式
2.若一次函数的图象与直线y=-3x+2交y轴于同一点,且过点(2,-6),求此函数解析式.
?
4.小明将父母给的零用钱按每月相等的数额存在储
蓄盒内,盒内钱数y(元)与存钱月数 x(月)之
间的关系如图所示.
(1)求y关于x的函数解析式;
(2)经过几个月小明才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
能力提升
(1)若直线y=kx+b与直线y=2x+1关于x轴对称,求k和b的值.
(2)若直线y=kx+b与直线y=2x+1关于y轴对称,求k和b的值.
由上面的结论,你能发现什么规律?
x
O
y
y=2x+1
