人教版八年级数学下册 第二十章 20.2数据的波动程度 课件(共39张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第二十章 20.2数据的波动程度 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 670.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:17:34 | ||
图片预览










文档简介
数据的波动程度
教学目标
经历方差的形成过程,了解方差的意义.?
掌握方差的计算方法并会初步运用方差解决实际问题,?
能熟练计算一组数据的方差.
教学重点
教学难点
方差意义的理解及应用.?
方差的应用、用样本估计总体.
方差的理解和计算.
想一想
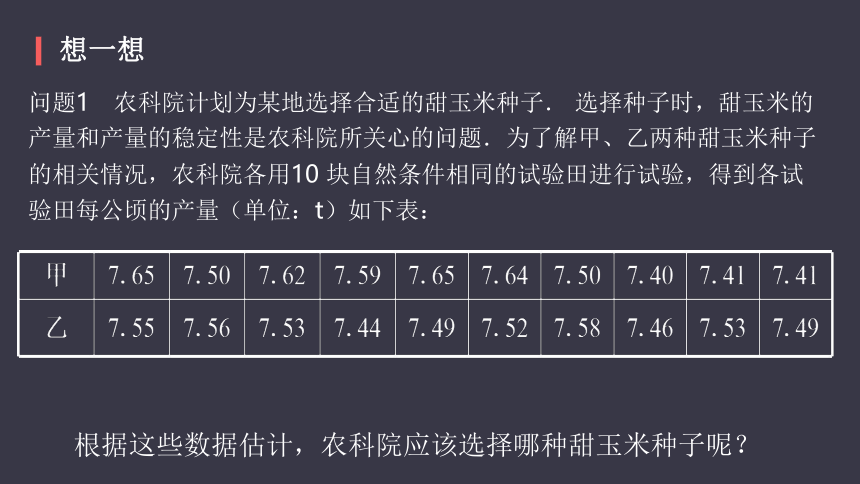
问题1 农科院计划为某地选择合适的甜玉米种子. 选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表:
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
想一想
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.?
一? ? ? ? ? ? ? ? ?一
可估计这个地区种植这两种甜玉米的平均产量相差不大.
想一想
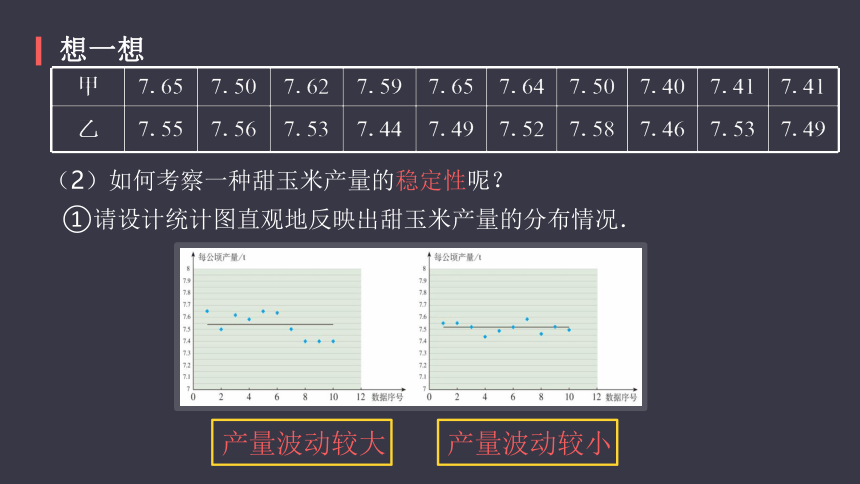
(2)如何考察一种甜玉米产量的稳定性呢???
产量波动较大
产量波动较小
①请设计统计图直观地反映出甜玉米产量的分布情况.
探究新知
②统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 (x1-x?)?,(x2-x?)??,
我们用这些值的平均数,即用
一? ? ? ? ? ? ? ? ? ? ? ? ? ??一
2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?2
一? ? ? ? ? ? ? ? ? ? ? 一? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??一
来衡量这组数据的波动大小,称它为这组数据的方差.
探究新知
一? ? ? ? ? ? ? ? ? ? ??一? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??一
当数据与平均数的差值越小时,
这些平方就越小,方差也就越小;
当数据与平均数的差值越大时,
这些平方就越大,方差也就越大.
方差越大,数据的波动越大;
方差越小,数据的波动越小.
探究新知
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
两组数据的方差分别是:
探究新知
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
显然 ? ? ? ,即说明甲种甜玉米的波动较大,这与
我们从产量分布图看到的结果一致.
据样本估计总体的统计思想,种乙种甜玉米产量较稳定.
例题
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如下表所示.
哪个芭蕾舞团女演员的身高更整齐?
例题
解:甲、乙两团演员的身高平均数分别是? 甲?
方差分别是
由? ? ? ? ? ? ? ? ?乙可知,甲芭蕾舞团女演员的身高更整齐。
一
一
用计算器求方差
使用计算器的统计功能可以求方差。使用计算器的统计功能求方差时,不同品牌的计算器的操作步骤有所不同,操作时需要参阅计算器的使用说明书。通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn;最后按动求方差的功能键(例如? ? ? ? 键),计算器便会求出方差的值.
一? ? ? ? ? ? ? ? ? 一? ? ? ? ? ? ? ? ? ? ? ?? 一
练习
1.用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的.
(1) 6? ? 6? ? 6? ? 6? ? 6? ? 6? ? 6;
(2) 5? ? 5? ? 6? ? 6? ? 6? ? 7? ? 7;
(3) 3? ? 3? ? 4? ? 6? ? 8? ? 9? ? 9;
(4) 3? ? 3? ? 3? ? 6? ? 9? ? 9? ? 9.
练习
2.如图是甲、乙两射击运动员的10
次射击训练成绩的折线统计图。观
察图形,甲、乙这10次射击成绩
的方差? ? ? ?,? ? ? ? ?乙哪个大?
知识引入
问题1 某快餐公司的香辣鸡腿很受消费者欢迎.现
有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两
家鸡腿的价格相同,品质相近.快餐公司决定通过检查
鸡腿的质量来确定选购哪家的鸡腿.
(1)可通过哪些统计量来关注鸡腿的质量?
(2)如何获取数据?
抽样调查.
每个鸡腿的质量;鸡腿质量的稳定性.
例题
在问题1 中,检查人员从两家的鸡腿中各随机抽取15 个,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
解:样本数据的平均数分别是:
一
一
样本平均数相同,估计这批鸡腿的平均质量相近.
例题
解:样本数据的平均数分别是:
由 ? ? ?可知,两家加工厂的鸡腿质量大致相等;
由 ? ? ? ? ?可知,甲加工厂的鸡腿质量更稳定,大小更均
匀.因此,快餐公司应该选购甲加工厂生产的鸡腿.
一? ? ? ? ??一
练习
某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛。下表是这两名运动员10次测验成绩(单位:m)
你认为应该选择哪名运动员参赛?为什么?
补充题
一台机床生产一种直径为40 mm的圆柱形零件,正常生产时直径的方差应不超过0.01 mm2,下表是某日8︰30—9︰30及10︰00—11︰00两个时段中各任意抽取10 件产品量出的直径的数值(单位:mm).
试判断在这两个时段内机床生产是否正常.如何对 生产作出评价?
复习巩固
1.甲、乙两台机床同时生产一种零件。在10天中,两台机床每天出次品的数量如下表:
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果看,在10天中,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
复习巩固
2.甲、乙两台包装机同时包装糖果。从中各抽出10袋,测得它们的实际质量(单位:g)如下表:
(1)分别计算两组数据的平均数和方差;
(2)哪台包装机包装的10袋糖果的质量比较稳定?
综合运用
3.为了考察甲、乙两种小麦的长势,分别从中随机抽取10株麦苗,测得苗高(单位:cm)如下表:
(1)分别计算两种小麦的平均苗高;
(2)哪种小麦的长势比较整齐?
综合运用
4.在体操比赛中,往往在所有裁判给出的分数中,去掉一个最高分和一个最低分然后计算余下分数的平均分.6个B组裁判员对某一运动员的打分数据(动作完成分)为:9.4,8.9,8.8,8.9,8.6,8.7.
(1)如果不去掉最高分和最低分,这组数据的平均数和方差分别是多少(结果保留小数点后两位)?
(2)如果去掉一个最高分和一个最低分,平均数和方差又分别是多少(结果保留小数点后两位)?
(3)你认为哪种统计平均分的方法更合理?
拓广探索
5.全班同学分成几个小组完成下面的活动:
(1)收集全班同学每个家庭在某个月的用水量
(2)将本组同学每个家庭在这个月的用水量作为样本数据,计算样本数据的平均数和方差,并根据样本数据的结论估计全班同学家庭用水量的情况;
(3)与其他小组进行交流,谈谈你对平均数、方差以及用样本估计总体的认识
总结
(1)方差怎样计算?
(2)你如何理解方差的意义?
(3)方差的适用条件:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
当两组数据的平均数相等或相近时,
才利用方差来判断它们的波动情况.
一? ? ? ? ? ? ? ? ?一? ? ? ? ? ? ? ? ? ? ? ? 一
关联数据的方差
关联数据的方差
C
数据波动程度的几种度量
这个式子可以用来度量数据的波动程度,我们把它叫做这组数据的平均差另一种做法是用方差?
来度量数据的波动程度
此外,人们还引入了标准差的概念。标准差是方差的算术平方根,即?
标准差的单位与原始数据的单位相同,实际中也常用它度量数据的波动程度.
一? ? ? ? ? ? ? ? ?一? ? ? ? ? ? ? ? ? ? ??一
一? ? ? ? ? ? ? ? ?一? ? ? ? ? ? ? ? ? ?? ? ?一
数据波动程度的几种度量
请同学们利用上面的几种度量数据波动程度的量解决下面的问题一个家具厂有甲、乙两个木料货源。下面是家具厂向两个货源订货后等待交货天数的样本数据.
分别计算样本数据的平均数、极差、平均差、方差和标准差。根据这些计算结果,看看家具厂从哪个货源进货比较好?为什么?
复习巩固
1.某水库为了解某种鱼的生长情况,从水库中捕捞了20条这种鱼,称得它们的质量(单位:kg)如下:
1.15 1.04 1.11 1.07 1.10 1.32 1.25 1.19 1.15 1.21
1.18 1.14 1.09 1.25 1.21 1.29 1.16 1.24 1.12 1.16
计算样本平均数(结果保留小数点后两位),并根据计算结果估计水库中这种鱼的平均质量.
复习巩固
这四个小组平均正确回答多少道题目(结果取整数)?
2.在一次智力请打比赛中,四个小组回答正确的情况下如下图:
复习巩固
3.为了解某一路口的汽车流量,调查了10天中同一时段通过该路口的汽车数量(单位:辆),结果如下:? ? ? ?
? ? 183? 209? 195? 178? 204? 215? 191? 208? 167? 197
在该时段中,平均约有多少辆汽车通过这个路口?
复习巩固
4.一家公司14名员工的月薪(单位:元)是:
8000? 6000? 2550? 1700? 2550? ? 4599? ? 4200
2550? 5100? 2500? 4400? 25000? 12400? 2500
(1)计算这组数据的平均数、中位数和众数;
(2)解释本题中平均数、中位数和众数的意义
复习巩固
5.某年A,B两座城市四季的平均气温(单位:℃)如下表
(1)分别计算A,B两座城市的年平均气温(结果取整数);
(2)哪座城市四季的平均气温较为接近?
综合运用
6.下表是两种股票一周内的交易日收盘价格(单位:元/股)。
计算它们的平均数和方差(结果保留小数点后两位),比较这两种股票在这段时间内的涨跌变化情况
综合运用
7.甲、乙两门大炮在相同条件下向同一目标各发射50发炮弹,炮弹落点情况如下表:
(1)分别计算两门大炮所发射的炮弹落点与目标的距离的平均数;
(2)哪门大炮射击的准确性好?
综合运用
8.为了促进学生参加体育锻炼,学校决定购买一批运动鞋供学生选购。请设计一个样本容量为30的调查方案进行调查,并计算样本的平均数、众数、中位数,为学校购买运动鞋提出建议.
拓广探索
9.统计全班同学上学所用时间,对所得数据进行整理、描述和分析,看看你能得出哪些结论.
教学目标
经历方差的形成过程,了解方差的意义.?
掌握方差的计算方法并会初步运用方差解决实际问题,?
能熟练计算一组数据的方差.
教学重点
教学难点
方差意义的理解及应用.?
方差的应用、用样本估计总体.
方差的理解和计算.
想一想
问题1 农科院计划为某地选择合适的甜玉米种子. 选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表:
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
想一想
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.?
一? ? ? ? ? ? ? ? ?一
可估计这个地区种植这两种甜玉米的平均产量相差不大.
想一想
(2)如何考察一种甜玉米产量的稳定性呢???
产量波动较大
产量波动较小
①请设计统计图直观地反映出甜玉米产量的分布情况.
探究新知
②统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 (x1-x?)?,(x2-x?)??,
我们用这些值的平均数,即用
一? ? ? ? ? ? ? ? ? ? ? ? ? ??一
2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?2
一? ? ? ? ? ? ? ? ? ? ? 一? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??一
来衡量这组数据的波动大小,称它为这组数据的方差.
探究新知
一? ? ? ? ? ? ? ? ? ? ??一? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??一
当数据与平均数的差值越小时,
这些平方就越小,方差也就越小;
当数据与平均数的差值越大时,
这些平方就越大,方差也就越大.
方差越大,数据的波动越大;
方差越小,数据的波动越小.
探究新知
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
两组数据的方差分别是:
探究新知
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
显然 ? ? ? ,即说明甲种甜玉米的波动较大,这与
我们从产量分布图看到的结果一致.
据样本估计总体的统计思想,种乙种甜玉米产量较稳定.
例题
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如下表所示.
哪个芭蕾舞团女演员的身高更整齐?
例题
解:甲、乙两团演员的身高平均数分别是? 甲?
方差分别是
由? ? ? ? ? ? ? ? ?乙可知,甲芭蕾舞团女演员的身高更整齐。
一
一
用计算器求方差
使用计算器的统计功能可以求方差。使用计算器的统计功能求方差时,不同品牌的计算器的操作步骤有所不同,操作时需要参阅计算器的使用说明书。通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn;最后按动求方差的功能键(例如? ? ? ? 键),计算器便会求出方差的值.
一? ? ? ? ? ? ? ? ? 一? ? ? ? ? ? ? ? ? ? ? ?? 一
练习
1.用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的.
(1) 6? ? 6? ? 6? ? 6? ? 6? ? 6? ? 6;
(2) 5? ? 5? ? 6? ? 6? ? 6? ? 7? ? 7;
(3) 3? ? 3? ? 4? ? 6? ? 8? ? 9? ? 9;
(4) 3? ? 3? ? 3? ? 6? ? 9? ? 9? ? 9.
练习
2.如图是甲、乙两射击运动员的10
次射击训练成绩的折线统计图。观
察图形,甲、乙这10次射击成绩
的方差? ? ? ?,? ? ? ? ?乙哪个大?
知识引入
问题1 某快餐公司的香辣鸡腿很受消费者欢迎.现
有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两
家鸡腿的价格相同,品质相近.快餐公司决定通过检查
鸡腿的质量来确定选购哪家的鸡腿.
(1)可通过哪些统计量来关注鸡腿的质量?
(2)如何获取数据?
抽样调查.
每个鸡腿的质量;鸡腿质量的稳定性.
例题
在问题1 中,检查人员从两家的鸡腿中各随机抽取15 个,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
解:样本数据的平均数分别是:
一
一
样本平均数相同,估计这批鸡腿的平均质量相近.
例题
解:样本数据的平均数分别是:
由 ? ? ?可知,两家加工厂的鸡腿质量大致相等;
由 ? ? ? ? ?可知,甲加工厂的鸡腿质量更稳定,大小更均
匀.因此,快餐公司应该选购甲加工厂生产的鸡腿.
一? ? ? ? ??一
练习
某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛。下表是这两名运动员10次测验成绩(单位:m)
你认为应该选择哪名运动员参赛?为什么?
补充题
一台机床生产一种直径为40 mm的圆柱形零件,正常生产时直径的方差应不超过0.01 mm2,下表是某日8︰30—9︰30及10︰00—11︰00两个时段中各任意抽取10 件产品量出的直径的数值(单位:mm).
试判断在这两个时段内机床生产是否正常.如何对 生产作出评价?
复习巩固
1.甲、乙两台机床同时生产一种零件。在10天中,两台机床每天出次品的数量如下表:
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果看,在10天中,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
复习巩固
2.甲、乙两台包装机同时包装糖果。从中各抽出10袋,测得它们的实际质量(单位:g)如下表:
(1)分别计算两组数据的平均数和方差;
(2)哪台包装机包装的10袋糖果的质量比较稳定?
综合运用
3.为了考察甲、乙两种小麦的长势,分别从中随机抽取10株麦苗,测得苗高(单位:cm)如下表:
(1)分别计算两种小麦的平均苗高;
(2)哪种小麦的长势比较整齐?
综合运用
4.在体操比赛中,往往在所有裁判给出的分数中,去掉一个最高分和一个最低分然后计算余下分数的平均分.6个B组裁判员对某一运动员的打分数据(动作完成分)为:9.4,8.9,8.8,8.9,8.6,8.7.
(1)如果不去掉最高分和最低分,这组数据的平均数和方差分别是多少(结果保留小数点后两位)?
(2)如果去掉一个最高分和一个最低分,平均数和方差又分别是多少(结果保留小数点后两位)?
(3)你认为哪种统计平均分的方法更合理?
拓广探索
5.全班同学分成几个小组完成下面的活动:
(1)收集全班同学每个家庭在某个月的用水量
(2)将本组同学每个家庭在这个月的用水量作为样本数据,计算样本数据的平均数和方差,并根据样本数据的结论估计全班同学家庭用水量的情况;
(3)与其他小组进行交流,谈谈你对平均数、方差以及用样本估计总体的认识
总结
(1)方差怎样计算?
(2)你如何理解方差的意义?
(3)方差的适用条件:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
当两组数据的平均数相等或相近时,
才利用方差来判断它们的波动情况.
一? ? ? ? ? ? ? ? ?一? ? ? ? ? ? ? ? ? ? ? ? 一
关联数据的方差
关联数据的方差
C
数据波动程度的几种度量
这个式子可以用来度量数据的波动程度,我们把它叫做这组数据的平均差另一种做法是用方差?
来度量数据的波动程度
此外,人们还引入了标准差的概念。标准差是方差的算术平方根,即?
标准差的单位与原始数据的单位相同,实际中也常用它度量数据的波动程度.
一? ? ? ? ? ? ? ? ?一? ? ? ? ? ? ? ? ? ? ??一
一? ? ? ? ? ? ? ? ?一? ? ? ? ? ? ? ? ? ?? ? ?一
数据波动程度的几种度量
请同学们利用上面的几种度量数据波动程度的量解决下面的问题一个家具厂有甲、乙两个木料货源。下面是家具厂向两个货源订货后等待交货天数的样本数据.
分别计算样本数据的平均数、极差、平均差、方差和标准差。根据这些计算结果,看看家具厂从哪个货源进货比较好?为什么?
复习巩固
1.某水库为了解某种鱼的生长情况,从水库中捕捞了20条这种鱼,称得它们的质量(单位:kg)如下:
1.15 1.04 1.11 1.07 1.10 1.32 1.25 1.19 1.15 1.21
1.18 1.14 1.09 1.25 1.21 1.29 1.16 1.24 1.12 1.16
计算样本平均数(结果保留小数点后两位),并根据计算结果估计水库中这种鱼的平均质量.
复习巩固
这四个小组平均正确回答多少道题目(结果取整数)?
2.在一次智力请打比赛中,四个小组回答正确的情况下如下图:
复习巩固
3.为了解某一路口的汽车流量,调查了10天中同一时段通过该路口的汽车数量(单位:辆),结果如下:? ? ? ?
? ? 183? 209? 195? 178? 204? 215? 191? 208? 167? 197
在该时段中,平均约有多少辆汽车通过这个路口?
复习巩固
4.一家公司14名员工的月薪(单位:元)是:
8000? 6000? 2550? 1700? 2550? ? 4599? ? 4200
2550? 5100? 2500? 4400? 25000? 12400? 2500
(1)计算这组数据的平均数、中位数和众数;
(2)解释本题中平均数、中位数和众数的意义
复习巩固
5.某年A,B两座城市四季的平均气温(单位:℃)如下表
(1)分别计算A,B两座城市的年平均气温(结果取整数);
(2)哪座城市四季的平均气温较为接近?
综合运用
6.下表是两种股票一周内的交易日收盘价格(单位:元/股)。
计算它们的平均数和方差(结果保留小数点后两位),比较这两种股票在这段时间内的涨跌变化情况
综合运用
7.甲、乙两门大炮在相同条件下向同一目标各发射50发炮弹,炮弹落点情况如下表:
(1)分别计算两门大炮所发射的炮弹落点与目标的距离的平均数;
(2)哪门大炮射击的准确性好?
综合运用
8.为了促进学生参加体育锻炼,学校决定购买一批运动鞋供学生选购。请设计一个样本容量为30的调查方案进行调查,并计算样本的平均数、众数、中位数,为学校购买运动鞋提出建议.
拓广探索
9.统计全班同学上学所用时间,对所得数据进行整理、描述和分析,看看你能得出哪些结论.
