人教版八年级数学下册第十八章:18.2.2菱形 课件(共59张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十八章:18.2.2菱形 课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:21:14 | ||
图片预览








文档简介
18.2.2菱形
理解菱形的概念,会用菱形的性质解决简单的问题.
教学目标
经历类比矩形探究菱形性质的过程,通过观察、类比、猜想、证明等活动,体会几何图形研究的一般步骤和方法.
掌握菱形的三种判定方法,能根据不同的已知条件,选择适当的判定定理进行推理和计算.
菱形性质的探索、证明和应用.
菱形判定条件的探索、证明和应用.
菱形的性质和判定的应用.
教学重点
教学重点
我们已经学习了特殊的平行四边形——矩形,?
它是从哪个角度特殊化来进行研究的??
它有哪些性质?
创设情境? 引出课题?
创设情境? 引出课题?
特殊化
平行四边形的性质
矩形的性质
对边相等
对角相等
对角线互相平分
对角线把平行四边形分成四个面积相等的三角形
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
创设情境? 引出课题?
平行四边形的角特殊化得到特殊的平行四边形——矩形;?
平行四边形的边特殊化,?
我们得到的特殊的平行四边形是什么??
它有什么特征?
菱形:一组邻边相等的平行四边形叫做菱形.
菱形的概念
符号语言:
∵四边形ABCD是平行四边形
且AB=BC
∴四边形ABCD是菱形
你能举出生活中的菱形的实际例子吗?
菱形的概念
菱形是特殊的平行四边形,?
因此它具有平行四边形的所有性质.?
类似于矩形,?
菱形是否也具有一般平行四边形不具有的特殊性质??
如果有,是什么?
探究菱形的性质
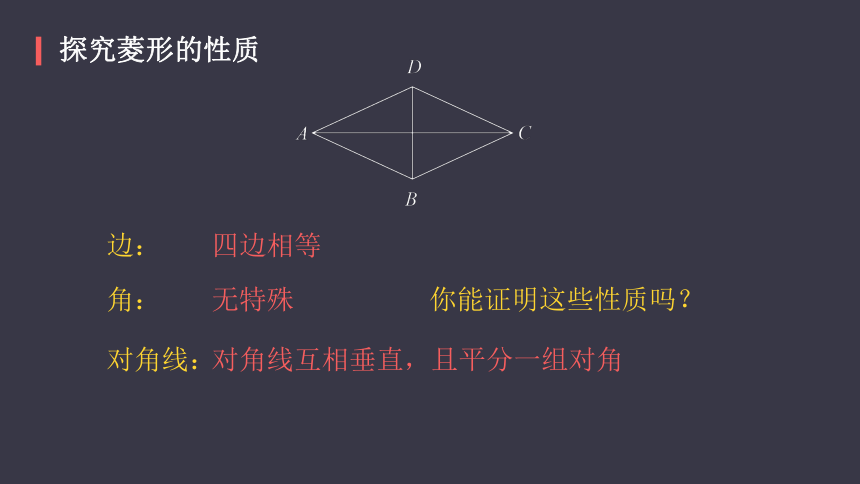
探究菱形的性质
边:
角:
对角线:
四边相等
无特殊
对角线互相垂直,且平分一组对角
你能证明这些性质吗?
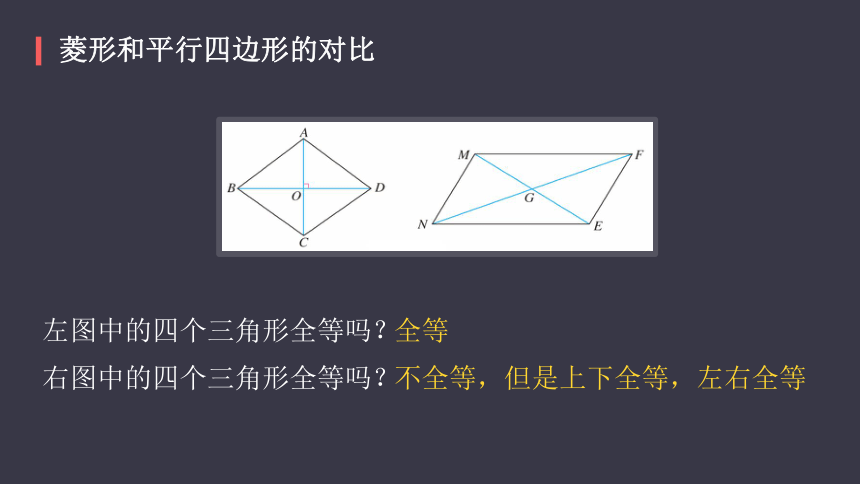
菱形和平行四边形的对比
左图中的四个三角形全等吗?
右图中的四个三角形全等吗?
全等
不全等,但是上下全等,左右全等
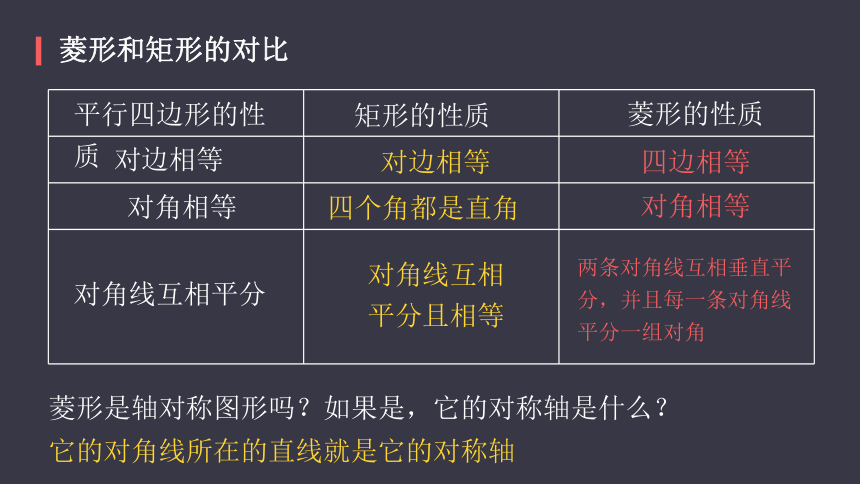
菱形和矩形的对比
菱形是轴对称图形吗?如果是,它的对称轴是什么?
它的对角线所在的直线就是它的对称轴
平行四边形的性质
对边相等
对角相等
对角线互相平分
矩形的性质
对边相等
四个角都是直角
对角线互相
平分且相等
菱形的性质
四边相等
对角相等
两条对角线互相垂直平分,并且每一条对角线平分一组对角
思考
如何利用折纸、剪切的方法既快又准确地剪出一个菱形的纸片?
小明是这样做的:将一张长方形的纸片对折,再对折,然后沿图中虚线剪下,打开即可,你知道其中的道理吗?
菱形的对角线与面积
由菱形两条对角线的长,
你能求出它的面积吗?
如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
例题
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
练习
2.已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积.
练习
判断对错:?
(1)菱形是平行四边形 ( )?
(2)有一组邻边相等的四边形是菱形 ( )?
(3)菱形的对角线互相平分且相等 ( )
练习
菱形的对称轴共有(? ? ?)?
A.1条? ? ? ? ?B.2条? ? ? ? C.3条? ? ? ? D.4条
练习
1.? ?已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中,∠BAD=60°,则∠ABD=______.
3.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是______.
练习?
在菱形 ABCD 中,对角线 AC ⊥ BD ,且 AC = 18 , BD = 10.则菱形 ABCD 的面积为______.
练习
90°
如图,在菱形ABCD中,若∠ABC=2∠BAD, 则∠BAD=______,△ABD为_______三角形.
练习
如图,在菱形ABCD中,若E是BD上任意一点,那么AE与CE 有怎样的数量关系?
练习
如图所示,菱形ABCD的周长为8 ,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=___________,菱形ABCD的面积S=_________.
练习
1:2
16
如图,菱形ABCD的一边中点M到对角线交点O 的距离为5cm,则菱形ABCD的周长为(? ? ? ? ?)
A. 5 cm? ? ?B. 10 cm? ? ? C. 20 cm? ? ? D. 40 cm
练习
D
如图,菱形ABCD的对角线AC、BD相交于点O, E、F分别是AD,
CD边上的中点,连接EF若EF=2,BD=6,则菱形ABCD的面积为________.
练习
12
如图所示,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,
AF⊥CD,垂足分别为E、F,连接EF,则△AEF的面积是(? ? ? ? )?
补充题
B
如图所示,在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为(? ? ? )
A.120°? ? ? ?B.100°? ? ? ? C.80°? ? ? ? D.60°
B
补充题
在任意四边形 ABCD 中,对角线 AC ⊥ BD ,且 AC = 18 , BD = 10 .你能求出四边形 ABCD 的面积吗?
补充题
如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC 于点E,则AE的长是(? ? ? )
求高问题
D
如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF 的长为(? ? ? ? ?)?
A.4? ? ? ? ? ?B.4.8? ? ? ? ? C.5? ? ? ? ? ?D.6
求高问题
B
求高问题
如图.在菱形ABCD中,对角线AC,BD交于点O,过点O作OH⊥AB,垂足为H,
(1)若∠ADC=130°,则∠AOH的大小为_________.
(2)若AC=8,BD=6,求OH的长.
答案:(1)65°;(2)
坐标系中的菱形
如图,四边形ABCD是菱形,A(3,0),B(0,4),则点c的坐标为(? ? ? )
A.(-5,4)? ? B.(-5,5)? ? C.(-4,4)? ? D.(-4,3)
A
坐标系中的菱形
菱形OACB在平面直角坐标系中的位置如图所示,点c的坐标是(6,0),点A的纵坐标是1,则点B的坐标是(? ? ?)?
A.(3,1)? ? ? B.(3,-1)? ? ? C.(1,-3)? ? ?D.(1,3)
B
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=BC,连结CE,
(1)求证:BD=EC;
(2)若∠E=60°,求∠BAO的度数;
(3)求证:S菱形=S△ABC
菱形性质的综合应用
回顾反思?类比猜想
我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?
定义
性质
回顾反思?类比猜想
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
有一组邻边相等的平行四边形是菱形
对角线互相平分的平行四边形是菱形
定义
性质
四条边都相等的四边形是菱形
推理论证?获得定理
猜想1:
对角线互相垂直的平行四边形是菱形.
如图, ABCD中,对角线AC,BD相交于点O,且AC⊥BD.求证: ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
推理论证?获得定理
符号语言:
∵在? ? ? ABCD中,AC⊥BD
∴? ? ? ABCD是菱形?
猜想2:
四条边相等的四边形是菱形
如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
推理论证?获得定理
推理论证?获得定理
四条边相等的四边形是菱形.
符号语言:
在四边形ABCD中,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形
例题
如图,? ?ABCD的对角线AC,BD相交于点O,且AB=5,AO=4,BO=3.求证: ABCD是菱形.
如图,用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?请说明理由.
练习
如图,先画两条等长的线段AB,AD,然后分别以B,D为圆心,AB长为半径画弧,两弧交点为C,连接BC,CD.得到的四边形ABCD是菱形吗?请说明理由.
练习
老师说下列三个图形都是菱形,你相信吗?
练习
练习
判断下列说法正误?
(1)对角线互相平分且邻边相等的四边形是菱形.?
(2)两组对边分别平行且一组邻边相等的四边形是菱形.?
(3)两组对角分别相等且对角线互相垂直的四边形是菱形.?
(4)对角线互相垂直平分的四边形是菱形.?
(5)对角线互相垂直的四边形是菱形.
练习
? ? ? ?ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则? ? ? ABCD是__________形;
(2)若AC=BD,则? ? ? ABCD是__________形;
(3)若∠ABC是直角,则? ? ? ABCD是__________形;
(4)若∠BAO=∠DAO,则? ? ? ABCD是_________形.
练习
下列条件中,不能判定四边形ABCD为菱形的是(? ? ?)
A.AC⊥BD,AC与BD互相平分
B. AB=BC=CD=DA?
C.AB=BC,AD=CD且AC⊥BD?
D.AB=CD,AD=BC,AC⊥BD
C
练习
如图,△ABC是等腰三角形,且AB=AC,把它沿底边BC翻折后,得△DBC.请你判断四边形ABDC的形状,并说明理由.
练习
1. 求证:??
?(1)对角线互相垂直的平行四边形是菱形;??
?(2)四条边相等的四边形是菱形.
练习
3.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
补充题
如图,AD平分∠BAC,DE//AC交AB于点E,DF//AB交AC于点F.求证:四边形AEDF是菱形.
补充题
如图,△ABC中,AB=AC,D是BC的中点,点E,F分别在AD及其延长线上,CE//BF,连接BE,CF.
求证:四边形BFCE是菱形.
补充题
如图, ABCD的对角线AC的垂直平分线与AD,BC分别交于点E,F.求证:四边形AFCE是菱形.
三个角是直角
总结
一组对边平行且相等
两组对边分别相等
两组对边分别平行
两组对角分别相等
对角线互相平分
对角线相等
一个角是直角
四条边都相等
一组邻边相等
对角线互相垂直
四边形
如图所示,在? ? ?ABCD中,E、F分别为边AB、 CD的中点,AC是对角线,过点B作BG//AC交DA的延长线与点G
(1)求证:CE//AF;
(2)若∠G=90°,求证四边形CEAF是菱形.
菱形的判定综合
菱形的判定综合
如图,在四边形ABCD中,AD//BC,对角线AC 、BD交于点O,过点O作直线EF交AD于点E,交BC于点F,OE=OF.
(1)求证AE=CF;
(2)当EF与BD满足什么位置关系时,四边形BFDE是菱形?请说明理由.
菱形的判定综合
如图,△ABC中,∠ACB=90°,BE平分
∠ABC,CD⊥AB于点D,EH⊥AB于点H,CD交BE于点F.求证:四边形CEHF为菱形.
如图,在平行四边形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
角平分线+平行
角平分线+平行
如图,△ABC中AB=AC,AD、CD是△ABC两个外角的平分线.
(1)求证:AC=AD;
(2)若∠B=60°,求证:四边形ABCD是菱形.
如图,在菱形ABCD中,∠ABC=120°E是AB边的中点,P是AC上的一个动点,PB+PE的最小值是? .求AB 的值.
线段和最小问题
答案:AB=2
如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,作第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边,作第三个菱形AB3C3D3,使
∠B3=60°;以此类推,这样作的第n个菱形 ABCD的边
ADn的长是____________.
菱形与找规律
如图,菱形ABCD的边长为2,BD=2,E, F分别是边AD,CD上的两个动点(E,F与D,C不重合),且满足AE+CF=2.
(1)求证:△BDE全等△BCF
(2)判断△BEF的形状,并说明理由
(3)设△BEF的面积为S,求S的取值范围.
菱形中等边三角形面积最值
答案(2)△BEF是等边三角形.
理解菱形的概念,会用菱形的性质解决简单的问题.
教学目标
经历类比矩形探究菱形性质的过程,通过观察、类比、猜想、证明等活动,体会几何图形研究的一般步骤和方法.
掌握菱形的三种判定方法,能根据不同的已知条件,选择适当的判定定理进行推理和计算.
菱形性质的探索、证明和应用.
菱形判定条件的探索、证明和应用.
菱形的性质和判定的应用.
教学重点
教学重点
我们已经学习了特殊的平行四边形——矩形,?
它是从哪个角度特殊化来进行研究的??
它有哪些性质?
创设情境? 引出课题?
创设情境? 引出课题?
特殊化
平行四边形的性质
矩形的性质
对边相等
对角相等
对角线互相平分
对角线把平行四边形分成四个面积相等的三角形
对边相等
四个角都是直角
对角线互相平分且相等
对角线把矩形分成四个
面积相等的等腰三角形
创设情境? 引出课题?
平行四边形的角特殊化得到特殊的平行四边形——矩形;?
平行四边形的边特殊化,?
我们得到的特殊的平行四边形是什么??
它有什么特征?
菱形:一组邻边相等的平行四边形叫做菱形.
菱形的概念
符号语言:
∵四边形ABCD是平行四边形
且AB=BC
∴四边形ABCD是菱形
你能举出生活中的菱形的实际例子吗?
菱形的概念
菱形是特殊的平行四边形,?
因此它具有平行四边形的所有性质.?
类似于矩形,?
菱形是否也具有一般平行四边形不具有的特殊性质??
如果有,是什么?
探究菱形的性质
探究菱形的性质
边:
角:
对角线:
四边相等
无特殊
对角线互相垂直,且平分一组对角
你能证明这些性质吗?
菱形和平行四边形的对比
左图中的四个三角形全等吗?
右图中的四个三角形全等吗?
全等
不全等,但是上下全等,左右全等
菱形和矩形的对比
菱形是轴对称图形吗?如果是,它的对称轴是什么?
它的对角线所在的直线就是它的对称轴
平行四边形的性质
对边相等
对角相等
对角线互相平分
矩形的性质
对边相等
四个角都是直角
对角线互相
平分且相等
菱形的性质
四边相等
对角相等
两条对角线互相垂直平分,并且每一条对角线平分一组对角
思考
如何利用折纸、剪切的方法既快又准确地剪出一个菱形的纸片?
小明是这样做的:将一张长方形的纸片对折,再对折,然后沿图中虚线剪下,打开即可,你知道其中的道理吗?
菱形的对角线与面积
由菱形两条对角线的长,
你能求出它的面积吗?
如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
例题
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
练习
2.已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积.
练习
判断对错:?
(1)菱形是平行四边形 ( )?
(2)有一组邻边相等的四边形是菱形 ( )?
(3)菱形的对角线互相平分且相等 ( )
练习
菱形的对称轴共有(? ? ?)?
A.1条? ? ? ? ?B.2条? ? ? ? C.3条? ? ? ? D.4条
练习
1.? ?已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中,∠BAD=60°,则∠ABD=______.
3.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是______.
练习?
在菱形 ABCD 中,对角线 AC ⊥ BD ,且 AC = 18 , BD = 10.则菱形 ABCD 的面积为______.
练习
90°
如图,在菱形ABCD中,若∠ABC=2∠BAD, 则∠BAD=______,△ABD为_______三角形.
练习
如图,在菱形ABCD中,若E是BD上任意一点,那么AE与CE 有怎样的数量关系?
练习
如图所示,菱形ABCD的周长为8 ,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=___________,菱形ABCD的面积S=_________.
练习
1:2
16
如图,菱形ABCD的一边中点M到对角线交点O 的距离为5cm,则菱形ABCD的周长为(? ? ? ? ?)
A. 5 cm? ? ?B. 10 cm? ? ? C. 20 cm? ? ? D. 40 cm
练习
D
如图,菱形ABCD的对角线AC、BD相交于点O, E、F分别是AD,
CD边上的中点,连接EF若EF=2,BD=6,则菱形ABCD的面积为________.
练习
12
如图所示,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,
AF⊥CD,垂足分别为E、F,连接EF,则△AEF的面积是(? ? ? ? )?
补充题
B
如图所示,在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为(? ? ? )
A.120°? ? ? ?B.100°? ? ? ? C.80°? ? ? ? D.60°
B
补充题
在任意四边形 ABCD 中,对角线 AC ⊥ BD ,且 AC = 18 , BD = 10 .你能求出四边形 ABCD 的面积吗?
补充题
如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC 于点E,则AE的长是(? ? ? )
求高问题
D
如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF 的长为(? ? ? ? ?)?
A.4? ? ? ? ? ?B.4.8? ? ? ? ? C.5? ? ? ? ? ?D.6
求高问题
B
求高问题
如图.在菱形ABCD中,对角线AC,BD交于点O,过点O作OH⊥AB,垂足为H,
(1)若∠ADC=130°,则∠AOH的大小为_________.
(2)若AC=8,BD=6,求OH的长.
答案:(1)65°;(2)
坐标系中的菱形
如图,四边形ABCD是菱形,A(3,0),B(0,4),则点c的坐标为(? ? ? )
A.(-5,4)? ? B.(-5,5)? ? C.(-4,4)? ? D.(-4,3)
A
坐标系中的菱形
菱形OACB在平面直角坐标系中的位置如图所示,点c的坐标是(6,0),点A的纵坐标是1,则点B的坐标是(? ? ?)?
A.(3,1)? ? ? B.(3,-1)? ? ? C.(1,-3)? ? ?D.(1,3)
B
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=BC,连结CE,
(1)求证:BD=EC;
(2)若∠E=60°,求∠BAO的度数;
(3)求证:S菱形=S△ABC
菱形性质的综合应用
回顾反思?类比猜想
我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?
定义
性质
回顾反思?类比猜想
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
有一组邻边相等的平行四边形是菱形
对角线互相平分的平行四边形是菱形
定义
性质
四条边都相等的四边形是菱形
推理论证?获得定理
猜想1:
对角线互相垂直的平行四边形是菱形.
如图, ABCD中,对角线AC,BD相交于点O,且AC⊥BD.求证: ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
推理论证?获得定理
符号语言:
∵在? ? ? ABCD中,AC⊥BD
∴? ? ? ABCD是菱形?
猜想2:
四条边相等的四边形是菱形
如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
推理论证?获得定理
推理论证?获得定理
四条边相等的四边形是菱形.
符号语言:
在四边形ABCD中,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形
例题
如图,? ?ABCD的对角线AC,BD相交于点O,且AB=5,AO=4,BO=3.求证: ABCD是菱形.
如图,用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?请说明理由.
练习
如图,先画两条等长的线段AB,AD,然后分别以B,D为圆心,AB长为半径画弧,两弧交点为C,连接BC,CD.得到的四边形ABCD是菱形吗?请说明理由.
练习
老师说下列三个图形都是菱形,你相信吗?
练习
练习
判断下列说法正误?
(1)对角线互相平分且邻边相等的四边形是菱形.?
(2)两组对边分别平行且一组邻边相等的四边形是菱形.?
(3)两组对角分别相等且对角线互相垂直的四边形是菱形.?
(4)对角线互相垂直平分的四边形是菱形.?
(5)对角线互相垂直的四边形是菱形.
练习
? ? ? ?ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则? ? ? ABCD是__________形;
(2)若AC=BD,则? ? ? ABCD是__________形;
(3)若∠ABC是直角,则? ? ? ABCD是__________形;
(4)若∠BAO=∠DAO,则? ? ? ABCD是_________形.
练习
下列条件中,不能判定四边形ABCD为菱形的是(? ? ?)
A.AC⊥BD,AC与BD互相平分
B. AB=BC=CD=DA?
C.AB=BC,AD=CD且AC⊥BD?
D.AB=CD,AD=BC,AC⊥BD
C
练习
如图,△ABC是等腰三角形,且AB=AC,把它沿底边BC翻折后,得△DBC.请你判断四边形ABDC的形状,并说明理由.
练习
1. 求证:??
?(1)对角线互相垂直的平行四边形是菱形;??
?(2)四条边相等的四边形是菱形.
练习
3.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
补充题
如图,AD平分∠BAC,DE//AC交AB于点E,DF//AB交AC于点F.求证:四边形AEDF是菱形.
补充题
如图,△ABC中,AB=AC,D是BC的中点,点E,F分别在AD及其延长线上,CE//BF,连接BE,CF.
求证:四边形BFCE是菱形.
补充题
如图, ABCD的对角线AC的垂直平分线与AD,BC分别交于点E,F.求证:四边形AFCE是菱形.
三个角是直角
总结
一组对边平行且相等
两组对边分别相等
两组对边分别平行
两组对角分别相等
对角线互相平分
对角线相等
一个角是直角
四条边都相等
一组邻边相等
对角线互相垂直
四边形
如图所示,在? ? ?ABCD中,E、F分别为边AB、 CD的中点,AC是对角线,过点B作BG//AC交DA的延长线与点G
(1)求证:CE//AF;
(2)若∠G=90°,求证四边形CEAF是菱形.
菱形的判定综合
菱形的判定综合
如图,在四边形ABCD中,AD//BC,对角线AC 、BD交于点O,过点O作直线EF交AD于点E,交BC于点F,OE=OF.
(1)求证AE=CF;
(2)当EF与BD满足什么位置关系时,四边形BFDE是菱形?请说明理由.
菱形的判定综合
如图,△ABC中,∠ACB=90°,BE平分
∠ABC,CD⊥AB于点D,EH⊥AB于点H,CD交BE于点F.求证:四边形CEHF为菱形.
如图,在平行四边形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
角平分线+平行
角平分线+平行
如图,△ABC中AB=AC,AD、CD是△ABC两个外角的平分线.
(1)求证:AC=AD;
(2)若∠B=60°,求证:四边形ABCD是菱形.
如图,在菱形ABCD中,∠ABC=120°E是AB边的中点,P是AC上的一个动点,PB+PE的最小值是? .求AB 的值.
线段和最小问题
答案:AB=2
如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,作第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边,作第三个菱形AB3C3D3,使
∠B3=60°;以此类推,这样作的第n个菱形 ABCD的边
ADn的长是____________.
菱形与找规律
如图,菱形ABCD的边长为2,BD=2,E, F分别是边AD,CD上的两个动点(E,F与D,C不重合),且满足AE+CF=2.
(1)求证:△BDE全等△BCF
(2)判断△BEF的形状,并说明理由
(3)设△BEF的面积为S,求S的取值范围.
菱形中等边三角形面积最值
答案(2)△BEF是等边三角形.
