人教版八年级数学下册第十八章:18.2.3正方形 课件(共59张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十八章:18.2.3正方形 课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 20:23:04 | ||
图片预览







文档简介
18.2.3正方形
理解正方形与平行四边形、矩形、菱形概念之间
的联系和区别.
能用正方形的定义、性质和判定进行推理与计算.
教学目标
正方形与平行四边形、矩形、菱形的联系.
正方形性质和判定的应用.
教学重点
教学难点
除了矩形和菱形外,还有什么特殊的平行四边形吗?
创设情境?引入新知
怎样研究这类图形?
先看看我们是怎样研究矩形和菱形的.
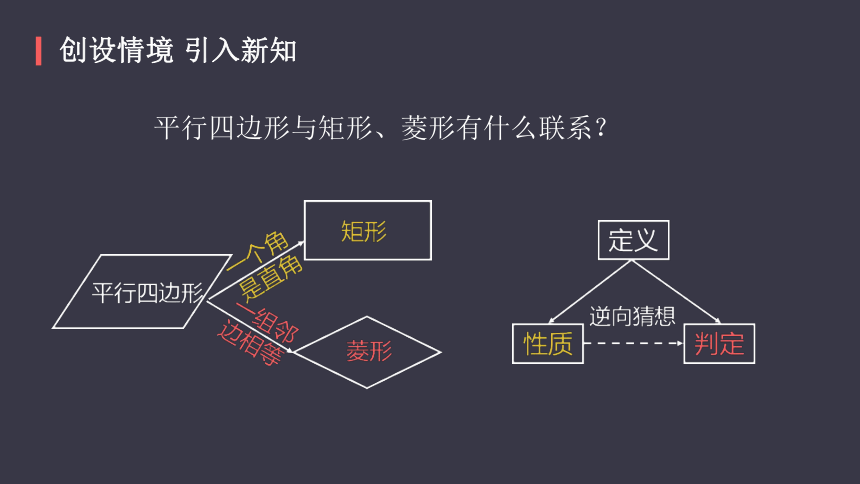
平行四边形与矩形、菱形有什么联系?
创设情境?引入新知
什么样的四边形是正方形? 你能下个定义吗?
四个角都是直角,四条边都相等的四边形叫正方形.
回顾思考?提出问题
不难发现,正方形既是矩形,又是菱形.
你能说说它有哪些性质吗?
边:
角:
对角线:
对称性:
四边相等
四个角都是直角
对角线互相平分线,垂直,相等,且平分对角
有四条对称轴
正方形的性质
求证:正方形的两条对角线把这个正方形分成四个全等的等腰三角形.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
证明:∵四边形ABCD是正方形, ∴AC=BD, AC⊥BD, AO=BO=CO=DO
∴△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
例题
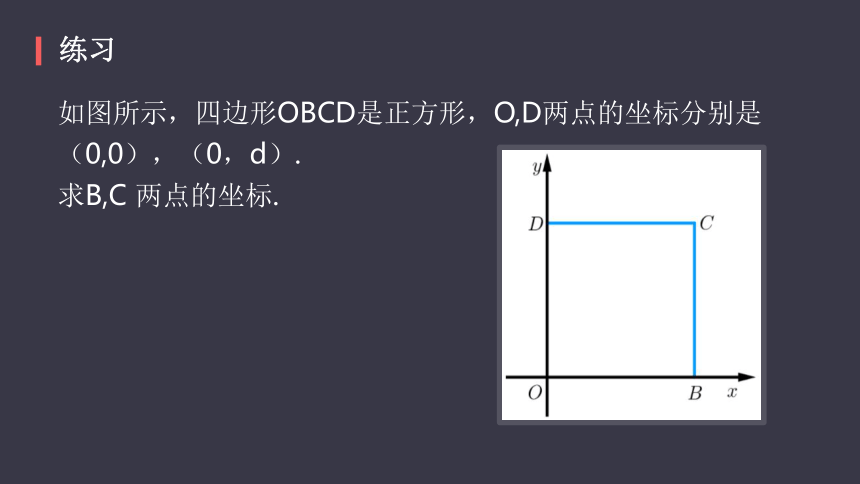
如图所示,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,d).
求B,C 两点的坐标.
练习
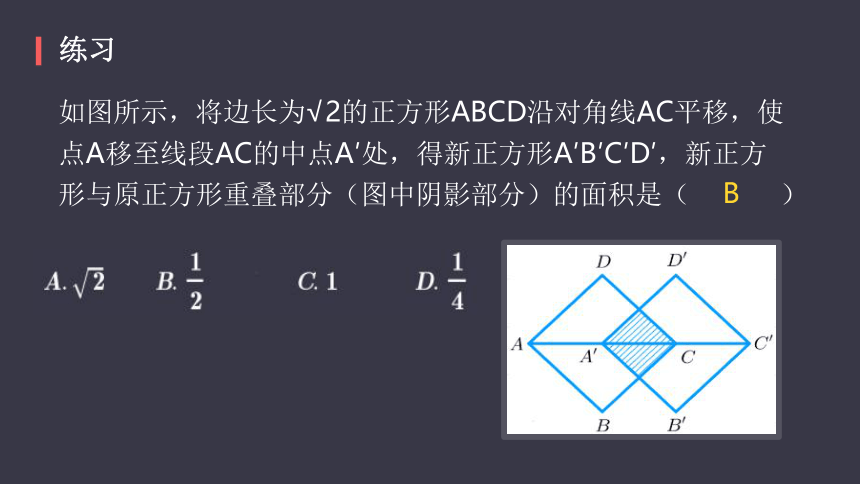
如图所示,将边长为√2的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是(? ? ? ? ? ?)
练习
B
练习
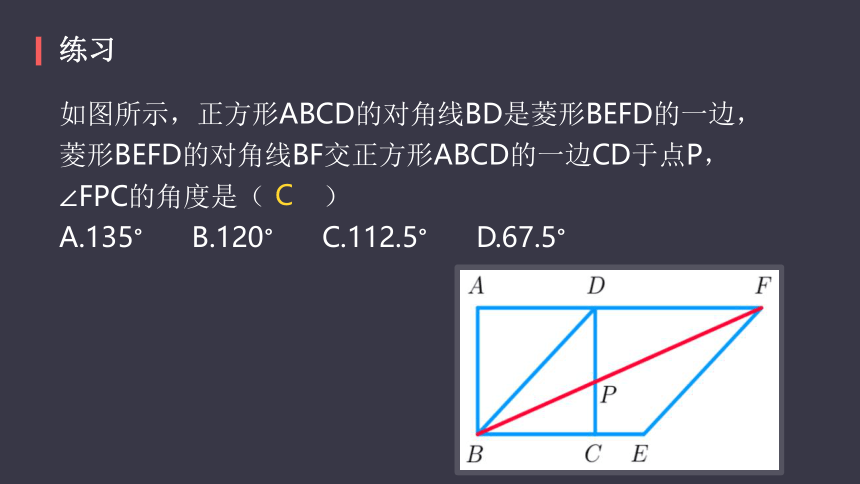
如图所示,正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线BF交正方形ABCD的一边CD于点P,∠FPC的角度是(? ? ? ?)
A.135°? ? ? B.120°? ? ? C.112.5°? ? ? D.67.5°
C
练习
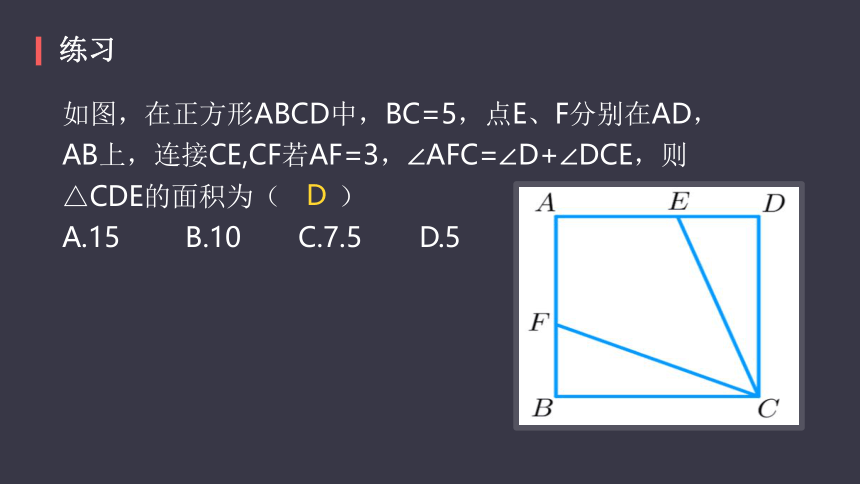
如图,在正方形ABCD中,BC=5,点E、F分别在AD, AB上,连接CE,CF若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为(? ? ? ?)
A.15? ? ? ? B.10? ? ? ?C.7.5? ? ? ?D.5
D
练习
已知:如图,在正方形ABCD中,点E在对角线AC上.
求证:BE=DE.
补充题
如图,ABCD是一个正方形花园,E,F是它的两个门,且DE=CF.要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?为什么?
答案:AF⊥BE
如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F,在线段AG上取点H,使得AG=DE+HG,连接BH,求证∠ABH=∠CDE.
补充题
如图,在正方形ABCD的外侧,作等边三角形ADE, AC,BE相交于点F,则∠BFC为(? ? ? ? )
A.45°? ? ? ?B.55°? ? ? ?C.60°? ? ? ?D.75°
补充题
C
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为(? ? ? ?)
补充题
C
你能用一张矩形纸片,折出一个最大的正方形吗?
思考
如图,某一拉门在完全关闭时,其相应的菱形变成正方形.请说说图中∠1的变化过程.
思考
如何判定一个四边形是正方形呢?
思考
正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下,并列表或用框图表示这些关系.
思考
正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下,并列表或用框图表示这些关系.
思考
如图,顺次连接正方形ABCD各边的中点,得到四边形EFGH.求证:四边形EFGH 也是正方形.
例题
例题
如图,E,F,G,H分别是各边上的点,且
AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
1.(1)把一张长方形纸片按如图方式折一下,就可以裁出正方形纸片。为什么?
(2)如何从一块长方形木板中裁出一块最大的正方形木板呢?
练习
2.如图,ABCD是一块正方形场地。小华和小芳在AB边上取定了一点E,测量知, EC=30m,EB=10m.这块场地的面积和对角线长分别是多少?
练习
练习
3.满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
练习
如图所示,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件:________________ ,使四边形ABCD是正方形(填一个即可)
练习
如图,把一个长方形纸片对折两次,然后沿图中虚线剪下一个角,为了得到一个正方形,剪切线与折痕所成的角的大小等于(? ? ? )
A.30°? ? ? ? ?B.45°? ? ? ? ?C.60°? ? ? ? ? D.90°
B
1.正方形的性质:
正方形既是矩形又是菱形,所以它具备所有矩形和菱形的性质.
2.正方形的判定:
总结
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为(? ? ? )
A.2? ? ? ? ?B.3? ? ? ? ?C.4? ? ? ? ?D.5
A
正方形半角模型
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG 的两直角边EF、BG分别交BC、DC 于点M、N.若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为(? ? ? ? ?)
正方形对角线上的直角
D
如图,P为正方形ABCD的对角线上任一点, PE⊥AB于点E,PF⊥BC于点F,判断DP与EF的关系,并证明.
正方形对称性的应用
如图将一边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为(? ? ? ?)
A.12? ? ? ? ? ?B.13? ? ? ? ? ?C.14? ? ? ? ? ?D.15
正方形内垂直的线段
B
已知如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值为(? ? ? ?)
A.10? ? ? ? ? ? ? B.8? ? ? ? ? ? ? ?C.6? ? ? ? ? ? ? ?D.12
线段和最小问题
A
线段和最小问题
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为(? ? ? )
C
线段和最小问题
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值(? ? ? ? ?)
C
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP 的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH 长度的最小值是______________.
隐藏圆
1.? 如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.它是一个矩形吗?为什么?
复习巩固
复习巩固
2. 求证:四个角都相等的四边形是矩形.
复习巩固
3.一个木匠要制作矩形的踏板。他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板。为什么?
复习巩固
4.? 在Rt△ABC中,∠C=90°,AB=2AC.求∠A,∠B的度数.
复习巩固
5.如图,四边形ABCD是菱形,∠ACD=30°,BD=6.求: (1)∠BAD,∠ABC 的度数;?
(2)AB,AC 的长.
复习巩固
6.如图,AE//BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD.求证:四边形ABCD是菱形.
7.如图,把一个长方形的纸片对折两次,然后剪下一个角.要得到一个正方形,剪口与折痕应成多少度的角?
综合应用
8.如图,为了做一个无盖纸盒,小明先在一块矩形硬纸板的四角画出四个相同的正方形,用剪刀剪下。然后把纸板的四边沿虛线折起,并用胶带粘好,一个无盖纸盒就做成了。纸盒的底面是什么形状?为什么?
综合应用
综合应用
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,∠ECD是多少度?为什么?
综合应用
10.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN ,MG//AD,NF//AB;点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN,EFCG 都是菱形.
综合应用
11. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H. 求DH的长.
综合应用
12.(1)如下页图(1),四边形OBCD是矩形,O,B,D三点的坐标分别是(0,0),(b,0),(0,d).求点C的坐标.
?(2)如下页图(2),四边形ABCD是菱形,C,D两点的坐标分别是(c,0),(0,d),点A,B在坐标轴上。求A,B两点的坐标.
(3)如下页图(3),四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,d)
求B,C 两点的坐标.
综合应用
13.如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
综合应用
14.如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长.
15.如图,四边形ABCD是正方形.G是BC上的任意一点,DE⊥AG于点E,BF//DE,且交AG于点F.
求证:AF-BF=EF.
拓广探索
拓广探索
16.如图,在△ABC中,BD,CE分别是边AC,AB上的中线, BD与CE相交于点O.BO与OD的长度有什么关系?BC边上的中线是否一定过点O?为什么?(提示:分别作BO,CO的中点M,N,连接ED,EM,MN,ND.)
拓广探索
17.如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,你有多少种方法?并与你的同学交流一下.
1.下面是两个有关正方形的小实验,想一想其中的道理: 如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等。无论正方形A1B1C1O 绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的? ? ? ,想一想,这是为什么.
丰富多彩的正方形
2.给你两个大小不等的正方形,你能通过切割把它们拼接成一个大正方形吗?(参考图2)说明你的拼法的道理.
丰富多彩的正方形
如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图1)
(1)对折矩形纸片ABCD,使AD与BC重合,
得到折痕EF,把纸片展平
(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.观察所得的∠ABM,∠MBN和∠NBC,这三个角有什么关系?你能证明吗?
通过证明可知,这是从矩形得到30°角的好方法,简单而准确。由此15°,60°,120°,150°等角就容易得到了.
折纸做60°、30°、15°的角
黄金矩形
宽与长的比(约为0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、匀称的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,如希腊的巴特农神庙(图2)等。
黄金矩形
下面我们折叠出一个黄金矩形:第一步,在一张矩形纸片的一端,利用图3的方法折出一个正方形,然后把纸片展平.
第二步,如图4,把这个正方形折成两个相等的矩形,再把纸片展平.
黄金矩形
第三步,折出内侧矩形的对角线AB,并把AB折到图5中所示的AD处.
第四步,展平纸片,按照所得的点D折出DE,矩形BCDE
(图6)就是黄金矩形.你能说明为什么吗?
(提示:设MN的长为2.)
1.选择题
(1)若平行四边形中两个内角的度数比为1:2,则其中较? ?小的内角是(? ? ?)??
? ? ? ?(A)90°? ?(B)60°? ?(C)120°? ?(D)45°
(2)若菱形的周长为8,高为1,则菱形两邻角的度数比为? ? ? (? ? ?)??
? ? ? (A)3:1? ? ?(B)4:1? ? ??
? ? ? (C)5:1? ? ?(D)6:1
复习巩固
复习巩固
(3)如图,在正方形ABCD的外侧,作等边三角形ADE,? ? ? ?则 ∠AEB为(? ? ? ? )??
? ? ? ?(A)10°? ? ? ?(B)15°? ? ? ?(C)20°? ? ? (D)125°
复习巩固
2.如图,将? ? ?ABCD的对角线BD向两个方向延长,分别至点?
? ?E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
复习巩固
3. 矩形对角线组成的对顶角中,有一组是两个50°的角.?对角线与各边组成的角是多少度?
复习巩固
4.? 如图,你能用一根绳子检查一个书架的侧边是否和上、下底都垂直吗?为什么?
复习巩固
5.? 如图,矩形ABCD的对角线AC,BD相交于点O,且 DE//AC,CE//BD.求证:四边形OCED是菱形.
6.? 如图,E,F,G,H分别是正方形ABCD各边的中点,四边形EFGH是什么四边形?为什么?
复习巩固
7. 如图,四边形ABCD是平行四边形,BE//DF,且分别交对角线AC于点E,F,连接ED,BF.求证∠1=∠2.
综合运用
8.如图,ABCD是一个正方形花园,E,F是它的两个门,且DE=CF.要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?为什么?
综合运用
综合运用
9.我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.
(1)任意四边形的中点四边形是什么形状?为什么?
(2)任意平行四边形的中点四边形是什么形状?为什么?
(3)任意矩形、菱形和正方形的中点四边形分别是什么形状?为什么?
综合运用
10.? 如果一个四边形是轴对称图形,并且有两条互相垂直的对称轴,它一定是菱形吗?一定是正方形吗?
综合运用
11.用纸板剪成的两个全等三角形能够拼成什么四边形?要想拼成一个矩形,需要两个什么样的全等三角形?要想拼成菱形或正方形呢?动手剪拼一下,并说明理由.
综合运用
12.如图,过? ? ? ABCD的对角线AC 的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H 四点,连接EF,FG,GH,HE.试判断四边形EFGH 的形状,并说明理由。
13.如图,在四边形ABCD中,AD//BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm.点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动。规定其中一个动点到达端点时,另一个动点也随之停止运动。从运动开始,使PQ//CD和PQ=CD,分别需经过多少时间?为什么?
拓广探索
14.如图,四边形ABCD是正方形,点E是边BC 的中点,∠AEF=90°,且EF交正方形外角的平分线CF 于点F.求证AE=EF.(提示:取AB 的中点G,连接EG.)
拓广探索
拓广探索
15.求证:平行四边形两条对角线的平方和等于四条边的平方和.
理解正方形与平行四边形、矩形、菱形概念之间
的联系和区别.
能用正方形的定义、性质和判定进行推理与计算.
教学目标
正方形与平行四边形、矩形、菱形的联系.
正方形性质和判定的应用.
教学重点
教学难点
除了矩形和菱形外,还有什么特殊的平行四边形吗?
创设情境?引入新知
怎样研究这类图形?
先看看我们是怎样研究矩形和菱形的.
平行四边形与矩形、菱形有什么联系?
创设情境?引入新知
什么样的四边形是正方形? 你能下个定义吗?
四个角都是直角,四条边都相等的四边形叫正方形.
回顾思考?提出问题
不难发现,正方形既是矩形,又是菱形.
你能说说它有哪些性质吗?
边:
角:
对角线:
对称性:
四边相等
四个角都是直角
对角线互相平分线,垂直,相等,且平分对角
有四条对称轴
正方形的性质
求证:正方形的两条对角线把这个正方形分成四个全等的等腰三角形.
已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.求证:△ABO,△BCO,△CDO,△DAO是全等的等腰直角三角形.
证明:∵四边形ABCD是正方形, ∴AC=BD, AC⊥BD, AO=BO=CO=DO
∴△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
例题
如图所示,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,d).
求B,C 两点的坐标.
练习
如图所示,将边长为√2的正方形ABCD沿对角线AC平移,使点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是(? ? ? ? ? ?)
练习
B
练习
如图所示,正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线BF交正方形ABCD的一边CD于点P,∠FPC的角度是(? ? ? ?)
A.135°? ? ? B.120°? ? ? C.112.5°? ? ? D.67.5°
C
练习
如图,在正方形ABCD中,BC=5,点E、F分别在AD, AB上,连接CE,CF若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为(? ? ? ?)
A.15? ? ? ? B.10? ? ? ?C.7.5? ? ? ?D.5
D
练习
已知:如图,在正方形ABCD中,点E在对角线AC上.
求证:BE=DE.
补充题
如图,ABCD是一个正方形花园,E,F是它的两个门,且DE=CF.要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?为什么?
答案:AF⊥BE
如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F,在线段AG上取点H,使得AG=DE+HG,连接BH,求证∠ABH=∠CDE.
补充题
如图,在正方形ABCD的外侧,作等边三角形ADE, AC,BE相交于点F,则∠BFC为(? ? ? ? )
A.45°? ? ? ?B.55°? ? ? ?C.60°? ? ? ?D.75°
补充题
C
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为(? ? ? ?)
补充题
C
你能用一张矩形纸片,折出一个最大的正方形吗?
思考
如图,某一拉门在完全关闭时,其相应的菱形变成正方形.请说说图中∠1的变化过程.
思考
如何判定一个四边形是正方形呢?
思考
正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下,并列表或用框图表示这些关系.
思考
正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下,并列表或用框图表示这些关系.
思考
如图,顺次连接正方形ABCD各边的中点,得到四边形EFGH.求证:四边形EFGH 也是正方形.
例题
例题
如图,E,F,G,H分别是各边上的点,且
AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
1.(1)把一张长方形纸片按如图方式折一下,就可以裁出正方形纸片。为什么?
(2)如何从一块长方形木板中裁出一块最大的正方形木板呢?
练习
2.如图,ABCD是一块正方形场地。小华和小芳在AB边上取定了一点E,测量知, EC=30m,EB=10m.这块场地的面积和对角线长分别是多少?
练习
练习
3.满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
练习
如图所示,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件:________________ ,使四边形ABCD是正方形(填一个即可)
练习
如图,把一个长方形纸片对折两次,然后沿图中虚线剪下一个角,为了得到一个正方形,剪切线与折痕所成的角的大小等于(? ? ? )
A.30°? ? ? ? ?B.45°? ? ? ? ?C.60°? ? ? ? ? D.90°
B
1.正方形的性质:
正方形既是矩形又是菱形,所以它具备所有矩形和菱形的性质.
2.正方形的判定:
总结
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为(? ? ? )
A.2? ? ? ? ?B.3? ? ? ? ?C.4? ? ? ? ?D.5
A
正方形半角模型
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG 的两直角边EF、BG分别交BC、DC 于点M、N.若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为(? ? ? ? ?)
正方形对角线上的直角
D
如图,P为正方形ABCD的对角线上任一点, PE⊥AB于点E,PF⊥BC于点F,判断DP与EF的关系,并证明.
正方形对称性的应用
如图将一边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为(? ? ? ?)
A.12? ? ? ? ? ?B.13? ? ? ? ? ?C.14? ? ? ? ? ?D.15
正方形内垂直的线段
B
已知如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,则DN+MN的最小值为(? ? ? ?)
A.10? ? ? ? ? ? ? B.8? ? ? ? ? ? ? ?C.6? ? ? ? ? ? ? ?D.12
线段和最小问题
A
线段和最小问题
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为(? ? ? )
C
线段和最小问题
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值(? ? ? ? ?)
C
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP 的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH 长度的最小值是______________.
隐藏圆
1.? 如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.它是一个矩形吗?为什么?
复习巩固
复习巩固
2. 求证:四个角都相等的四边形是矩形.
复习巩固
3.一个木匠要制作矩形的踏板。他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板。为什么?
复习巩固
4.? 在Rt△ABC中,∠C=90°,AB=2AC.求∠A,∠B的度数.
复习巩固
5.如图,四边形ABCD是菱形,∠ACD=30°,BD=6.求: (1)∠BAD,∠ABC 的度数;?
(2)AB,AC 的长.
复习巩固
6.如图,AE//BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD.求证:四边形ABCD是菱形.
7.如图,把一个长方形的纸片对折两次,然后剪下一个角.要得到一个正方形,剪口与折痕应成多少度的角?
综合应用
8.如图,为了做一个无盖纸盒,小明先在一块矩形硬纸板的四角画出四个相同的正方形,用剪刀剪下。然后把纸板的四边沿虛线折起,并用胶带粘好,一个无盖纸盒就做成了。纸盒的底面是什么形状?为什么?
综合应用
综合应用
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,∠ECD是多少度?为什么?
综合应用
10.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN ,MG//AD,NF//AB;点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN,EFCG 都是菱形.
综合应用
11. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H. 求DH的长.
综合应用
12.(1)如下页图(1),四边形OBCD是矩形,O,B,D三点的坐标分别是(0,0),(b,0),(0,d).求点C的坐标.
?(2)如下页图(2),四边形ABCD是菱形,C,D两点的坐标分别是(c,0),(0,d),点A,B在坐标轴上。求A,B两点的坐标.
(3)如下页图(3),四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,d)
求B,C 两点的坐标.
综合应用
13.如图,E,F,M,N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
综合应用
14.如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长.
15.如图,四边形ABCD是正方形.G是BC上的任意一点,DE⊥AG于点E,BF//DE,且交AG于点F.
求证:AF-BF=EF.
拓广探索
拓广探索
16.如图,在△ABC中,BD,CE分别是边AC,AB上的中线, BD与CE相交于点O.BO与OD的长度有什么关系?BC边上的中线是否一定过点O?为什么?(提示:分别作BO,CO的中点M,N,连接ED,EM,MN,ND.)
拓广探索
17.如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,你有多少种方法?并与你的同学交流一下.
1.下面是两个有关正方形的小实验,想一想其中的道理: 如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等。无论正方形A1B1C1O 绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的? ? ? ,想一想,这是为什么.
丰富多彩的正方形
2.给你两个大小不等的正方形,你能通过切割把它们拼接成一个大正方形吗?(参考图2)说明你的拼法的道理.
丰富多彩的正方形
如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图1)
(1)对折矩形纸片ABCD,使AD与BC重合,
得到折痕EF,把纸片展平
(2)再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM.同时,得到了线段BN.观察所得的∠ABM,∠MBN和∠NBC,这三个角有什么关系?你能证明吗?
通过证明可知,这是从矩形得到30°角的好方法,简单而准确。由此15°,60°,120°,150°等角就容易得到了.
折纸做60°、30°、15°的角
黄金矩形
宽与长的比(约为0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、匀称的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,如希腊的巴特农神庙(图2)等。
黄金矩形
下面我们折叠出一个黄金矩形:第一步,在一张矩形纸片的一端,利用图3的方法折出一个正方形,然后把纸片展平.
第二步,如图4,把这个正方形折成两个相等的矩形,再把纸片展平.
黄金矩形
第三步,折出内侧矩形的对角线AB,并把AB折到图5中所示的AD处.
第四步,展平纸片,按照所得的点D折出DE,矩形BCDE
(图6)就是黄金矩形.你能说明为什么吗?
(提示:设MN的长为2.)
1.选择题
(1)若平行四边形中两个内角的度数比为1:2,则其中较? ?小的内角是(? ? ?)??
? ? ? ?(A)90°? ?(B)60°? ?(C)120°? ?(D)45°
(2)若菱形的周长为8,高为1,则菱形两邻角的度数比为? ? ? (? ? ?)??
? ? ? (A)3:1? ? ?(B)4:1? ? ??
? ? ? (C)5:1? ? ?(D)6:1
复习巩固
复习巩固
(3)如图,在正方形ABCD的外侧,作等边三角形ADE,? ? ? ?则 ∠AEB为(? ? ? ? )??
? ? ? ?(A)10°? ? ? ?(B)15°? ? ? ?(C)20°? ? ? (D)125°
复习巩固
2.如图,将? ? ?ABCD的对角线BD向两个方向延长,分别至点?
? ?E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
复习巩固
3. 矩形对角线组成的对顶角中,有一组是两个50°的角.?对角线与各边组成的角是多少度?
复习巩固
4.? 如图,你能用一根绳子检查一个书架的侧边是否和上、下底都垂直吗?为什么?
复习巩固
5.? 如图,矩形ABCD的对角线AC,BD相交于点O,且 DE//AC,CE//BD.求证:四边形OCED是菱形.
6.? 如图,E,F,G,H分别是正方形ABCD各边的中点,四边形EFGH是什么四边形?为什么?
复习巩固
7. 如图,四边形ABCD是平行四边形,BE//DF,且分别交对角线AC于点E,F,连接ED,BF.求证∠1=∠2.
综合运用
8.如图,ABCD是一个正方形花园,E,F是它的两个门,且DE=CF.要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?为什么?
综合运用
综合运用
9.我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.
(1)任意四边形的中点四边形是什么形状?为什么?
(2)任意平行四边形的中点四边形是什么形状?为什么?
(3)任意矩形、菱形和正方形的中点四边形分别是什么形状?为什么?
综合运用
10.? 如果一个四边形是轴对称图形,并且有两条互相垂直的对称轴,它一定是菱形吗?一定是正方形吗?
综合运用
11.用纸板剪成的两个全等三角形能够拼成什么四边形?要想拼成一个矩形,需要两个什么样的全等三角形?要想拼成菱形或正方形呢?动手剪拼一下,并说明理由.
综合运用
12.如图,过? ? ? ABCD的对角线AC 的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H 四点,连接EF,FG,GH,HE.试判断四边形EFGH 的形状,并说明理由。
13.如图,在四边形ABCD中,AD//BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm.点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动。规定其中一个动点到达端点时,另一个动点也随之停止运动。从运动开始,使PQ//CD和PQ=CD,分别需经过多少时间?为什么?
拓广探索
14.如图,四边形ABCD是正方形,点E是边BC 的中点,∠AEF=90°,且EF交正方形外角的平分线CF 于点F.求证AE=EF.(提示:取AB 的中点G,连接EG.)
拓广探索
拓广探索
15.求证:平行四边形两条对角线的平方和等于四条边的平方和.
