人教版八年级数学下册第十九章:19.2.1正比例函数 课件(共38张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十九章:19.2.1正比例函数 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:40:55 | ||
图片预览











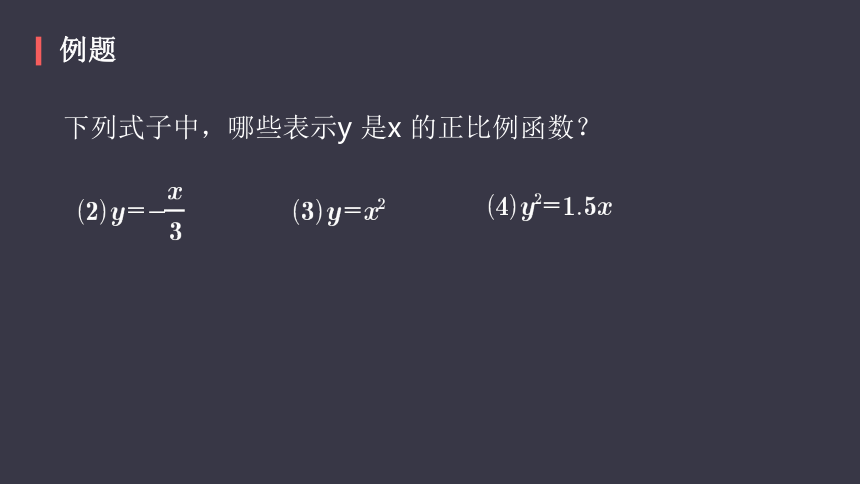
文档简介
正比例函数
教学目标
理解正比例函数的概念.?
经历用函数解析式表示函数关系的过程,进一步
发展符号意识;经历从一类具体函数中抽象出正比例函数概念的过程,发展数学抽象概括能力.?
会画正比例函数的图象.?
能根据正比例函数的图象和表达式
y
=kx(k≠0)
理解k>0和k<0时,函数的图象特征与增减性.
教学重点
正比例函数的概念.?
用数形结合的思想方法,通过画图观察,概括正比例函数的图象特征及性质.
教学难点
正比例函数图象的性质及应用.
思考
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:
(2)如果从小学学习过的比例观点看,列车在运行过程中,行程
y(单位:km)和运行时间
t(单位:h)是什么关系?
思考
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:?
(3)如果从函数的观点看,京沪高铁列车的行程
y
(单位:km)是运行时间
t(单位:h)的函数吗?能写
出这个函数的解析式,并写出自变量的取值范围吗??
思考
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:?
(4)乘京沪高铁列车从北京南站出发2.5
h后,是否已经过了距始发站1
100
km
的南京南站??
思考
思考
这个问题中得到的函数解析式有什么特点??
?
函数值与对应的自变量的值的比有什么特点?
?
思考
问题2 下列问题中,变量之间的对应关系是函数关
系吗?如果是,请写出函数解析式.
(1)圆的周长
l
随半径
r
的变化而变化;
(2)铁的密度为7.8
g/cm3,铁块的质量
m(单位:g)随它的体积
V(单位:cm3)的变化而变化;
l=2πr
m=7.8V
思考
问题2 下列问题中,变量之间的对应关系是函数关
系吗?如果是,请写出函数解析式.
(3)每个练习本的厚度为0.5
cm,练习本摞在一起的
总厚度
h(单位:cm)随练习本的本数
n
变化而变化;
(4)冷冻一个0
℃
的物体,使它每分下降2
℃,物体
的温度
T(单位:℃)随冷冻时间
t(单位:min)的变化而变化.
h=0.5n
T=-2t
观察总结
形成概念
认真观察这四个函数解析式,说说这些函数有什么
共同点.
h=0.5n
T=-2t
l=2πr
m=7.8V
一般地,形如y=kx(k
是常数,k≠0)的函数,
叫做正比例函数,其中k
叫做比例系数.
例题
下列式子中,哪些表示y
是x
的正比例函数?
练习
下列式子中,哪些表示y
是x
的正比例函数?
练习
2.列式表示下列问题中的y与x的函数关系,并指出哪些是正比例函数.
(1)正方形的边长为xcm,周长为ycm;
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元;
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm,体积为y?
????
补充题
若?
?
?
?
?
?
?
?
?
?
是正比例函数,则m=______________
补充题
若?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
是正比例函数,则m=______________
-2
补充题
若y=(k+1)x+k-1是正比例函数,求函数解析式
答案:y=2x
补充题
若函数y=(m-2)x?
?
?
?
是正比例函数,那么(?
?
)
A.M=2或M=0?
?
?
?
?
?
?
?
?
?B.M=2
C.M=0?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
D.M=1
C
例题
y与x成正比例,且当x=2时,y=6,求y与x的函数解析式
?.
∵y与x成正比例,
设y=kx(k≠0)
∵当x=2时,y=6,
∴6=2k
解k=3.
∴y=3x
例题
已知y与x-3成正比例,当x=4时,y=3.
(1)求这个函数解析式
?.
(2)求当x=3时y的值.
练习
y与2x成正比例,且当x=3时,y=12,求y与x的函数解析式.
答案:y=4x
练习
y-2与x成正比例,且当x=3时,y=1,求y与x的函数关系式,并判断它是不是正比例函数.
知识回顾
描点法画函数图象一般步骤:
列表
描点
连线
例题
画出下列正比正比例函数的图象:
(1)y=2x,y=?
?
?x?
?
?
?
(2)y=-1.5x,y=-4x?
观察图象
归纳性质
正比例函数的图象都是过______的____线.
k>0时,过____、____象限,y随x的增大而______.
K<0时,过____、____象限,y随x的增大而______.
正比例函数的图象与性质
怎么画正比例函数的图象???
正比例函数的图象有哪些性质?
正比例函数图象的简单画法
我们知道,正比例函数的图象是一条经过
坐标原点的直线,我们也知道,两点确定一条直线,现在,我们有画正比例函数图象的简便画法了吗?
过原点(0,0)和点(1,k)画直线,
得到y
=kx
的图象.
练习
用你认为最近的的方法画出下列函数的图象:
(1)y=?3x?
?
?
?
(2)y=-3x?
练习
函数y=-25x的图象经过第___________
象限,经过点
(0,___________?)与点(1,___________)?,y随x的增大而__________??函数y=?4x的图象经过第___________??象限,经过点(0,___________?)与点(1,___________?),y随x的增大而___________.??
练习
已知点A(-1,y1),B(3,y2)都在直线y=-5x上,
则y1与y2的关系是(?
?
?
?
)
A.?
y1≤y2
?
?
?
?
?
?
?
?
?
B.
?y1=y2
?
?
?
?
?
?
??
C
.?
y1?
?
?
?
?
?
?
?
?D
.
y1>y2
D
练面直角坐标系中,正比例函数y
=kx(k<0)的图象的大致位置只可能是( )
A
练习
对于正比例函数y
=kx,当x
增大时,y
随x
的增大而增大,则k的取值范围
(?
?
?
?
?
?)
A.k<0 B.k≤0
C.k>0 D.k≥0
C
补充题
函数y
=-x(x<0)的图象是(?
?
)
C
补充题
比较大小:
(1)k1_________k2;(2)k3
_________k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
k1<k2
<k3
<k4
<
<
例题
如图,正比例函数y=kx图象经过点A,该函数解析式是________.
y=kx
练习
若直线y=k经过点A(-5,3),则k_____________;
如
果这条直线上点B的横坐标wB=4,那么它的纵坐
标______________.?
补充题
已知正比例函数y=4x图象上有一点P(x,y)和一点A(6,0
),O为坐标原点
,且△PAO的面积等于12,求点P的坐标。
答案:?
?
?
(1,4),?
?
?
?(-1,-4)
总结
正比例函数的概念:?
?
正比例函数图象的性质:??
解析式的求法:
?
y=kx(k≠0)
正比例函数的图象都是过原点的直线.
k>0时,过一、三象限,y随x的增大而增大.
K<0时,过二、四象限,y随x的增大而减小.
关键是把点坐标代入解析式
教学目标
理解正比例函数的概念.?
经历用函数解析式表示函数关系的过程,进一步
发展符号意识;经历从一类具体函数中抽象出正比例函数概念的过程,发展数学抽象概括能力.?
会画正比例函数的图象.?
能根据正比例函数的图象和表达式
y
=kx(k≠0)
理解k>0和k<0时,函数的图象特征与增减性.
教学重点
正比例函数的概念.?
用数形结合的思想方法,通过画图观察,概括正比例函数的图象特征及性质.
教学难点
正比例函数图象的性质及应用.
思考
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:
(2)如果从小学学习过的比例观点看,列车在运行过程中,行程
y(单位:km)和运行时间
t(单位:h)是什么关系?
思考
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:?
(3)如果从函数的观点看,京沪高铁列车的行程
y
(单位:km)是运行时间
t(单位:h)的函数吗?能写
出这个函数的解析式,并写出自变量的取值范围吗??
思考
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:?
(4)乘京沪高铁列车从北京南站出发2.5
h后,是否已经过了距始发站1
100
km
的南京南站??
思考
思考
这个问题中得到的函数解析式有什么特点??
?
函数值与对应的自变量的值的比有什么特点?
?
思考
问题2 下列问题中,变量之间的对应关系是函数关
系吗?如果是,请写出函数解析式.
(1)圆的周长
l
随半径
r
的变化而变化;
(2)铁的密度为7.8
g/cm3,铁块的质量
m(单位:g)随它的体积
V(单位:cm3)的变化而变化;
l=2πr
m=7.8V
思考
问题2 下列问题中,变量之间的对应关系是函数关
系吗?如果是,请写出函数解析式.
(3)每个练习本的厚度为0.5
cm,练习本摞在一起的
总厚度
h(单位:cm)随练习本的本数
n
变化而变化;
(4)冷冻一个0
℃
的物体,使它每分下降2
℃,物体
的温度
T(单位:℃)随冷冻时间
t(单位:min)的变化而变化.
h=0.5n
T=-2t
观察总结
形成概念
认真观察这四个函数解析式,说说这些函数有什么
共同点.
h=0.5n
T=-2t
l=2πr
m=7.8V
一般地,形如y=kx(k
是常数,k≠0)的函数,
叫做正比例函数,其中k
叫做比例系数.
例题
下列式子中,哪些表示y
是x
的正比例函数?
练习
下列式子中,哪些表示y
是x
的正比例函数?
练习
2.列式表示下列问题中的y与x的函数关系,并指出哪些是正比例函数.
(1)正方形的边长为xcm,周长为ycm;
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元;
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm,体积为y?
????
补充题
若?
?
?
?
?
?
?
?
?
?
是正比例函数,则m=______________
补充题
若?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
是正比例函数,则m=______________
-2
补充题
若y=(k+1)x+k-1是正比例函数,求函数解析式
答案:y=2x
补充题
若函数y=(m-2)x?
?
?
?
是正比例函数,那么(?
?
)
A.M=2或M=0?
?
?
?
?
?
?
?
?
?B.M=2
C.M=0?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
D.M=1
C
例题
y与x成正比例,且当x=2时,y=6,求y与x的函数解析式
?.
∵y与x成正比例,
设y=kx(k≠0)
∵当x=2时,y=6,
∴6=2k
解k=3.
∴y=3x
例题
已知y与x-3成正比例,当x=4时,y=3.
(1)求这个函数解析式
?.
(2)求当x=3时y的值.
练习
y与2x成正比例,且当x=3时,y=12,求y与x的函数解析式.
答案:y=4x
练习
y-2与x成正比例,且当x=3时,y=1,求y与x的函数关系式,并判断它是不是正比例函数.
知识回顾
描点法画函数图象一般步骤:
列表
描点
连线
例题
画出下列正比正比例函数的图象:
(1)y=2x,y=?
?
?x?
?
?
?
(2)y=-1.5x,y=-4x?
观察图象
归纳性质
正比例函数的图象都是过______的____线.
k>0时,过____、____象限,y随x的增大而______.
K<0时,过____、____象限,y随x的增大而______.
正比例函数的图象与性质
怎么画正比例函数的图象???
正比例函数的图象有哪些性质?
正比例函数图象的简单画法
我们知道,正比例函数的图象是一条经过
坐标原点的直线,我们也知道,两点确定一条直线,现在,我们有画正比例函数图象的简便画法了吗?
过原点(0,0)和点(1,k)画直线,
得到y
=kx
的图象.
练习
用你认为最近的的方法画出下列函数的图象:
(1)y=?3x?
?
?
?
(2)y=-3x?
练习
函数y=-25x的图象经过第___________
象限,经过点
(0,___________?)与点(1,___________)?,y随x的增大而__________??函数y=?4x的图象经过第___________??象限,经过点(0,___________?)与点(1,___________?),y随x的增大而___________.??
练习
已知点A(-1,y1),B(3,y2)都在直线y=-5x上,
则y1与y2的关系是(?
?
?
?
)
A.?
y1≤y2
?
?
?
?
?
?
?
?
?
B.
?y1=y2
?
?
?
?
?
?
??
C
.?
y1
?
?
?
?
?
?
?
?D
.
y1>y2
D
练面直角坐标系中,正比例函数y
=kx(k<0)的图象的大致位置只可能是( )
A
练习
对于正比例函数y
=kx,当x
增大时,y
随x
的增大而增大,则k的取值范围
(?
?
?
?
?
?)
A.k<0 B.k≤0
C.k>0 D.k≥0
C
补充题
函数y
=-x(x<0)的图象是(?
?
)
C
补充题
比较大小:
(1)k1_________k2;(2)k3
_________k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
k1<k2
<k3
<k4
<
<
例题
如图,正比例函数y=kx图象经过点A,该函数解析式是________.
y=kx
练习
若直线y=k经过点A(-5,3),则k_____________;
如
果这条直线上点B的横坐标wB=4,那么它的纵坐
标______________.?
补充题
已知正比例函数y=4x图象上有一点P(x,y)和一点A(6,0
),O为坐标原点
,且△PAO的面积等于12,求点P的坐标。
答案:?
?
?
(1,4),?
?
?
?(-1,-4)
总结
正比例函数的概念:?
?
正比例函数图象的性质:??
解析式的求法:
?
y=kx(k≠0)
正比例函数的图象都是过原点的直线.
k>0时,过一、三象限,y随x的增大而增大.
K<0时,过二、四象限,y随x的增大而减小.
关键是把点坐标代入解析式
