人教版八年级数学下册第十九章:19.2一次函数的应用 课件(共31张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十九章:19.2一次函数的应用 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 545.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览









文档简介
一次函数的应用
教学目标
学会用待定系数法求一次函数解析式.
了解分段函数的表示及其图象,?
能初步应用一次函数模型解决现实生活中的问题,体会一次函数的应用价值.
教学重点
用待定系数法求一次函数解析式.?
初步了解分段函数.
一次函数的应用.
教学难点
思考
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
y=x-1
y=-2x+3
两点法——两点确定一条直线
反过来已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
例题
已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:求一次函数y=kx+b的解析式,关键是求出k,b的值。从已知条件可以列出关于k,b的二元一次方程组,并求出k,b
这种求解析式的方法,
叫做待定系数法.
解:设这个一次函数的解析式为y=kx+b
因为y=kx+b的图象过点(3,5)与(-4,-9),所以 解方程组得 {
这个一次函数的解析式为y=2x-1
3k+b=5 ①
-4k+b=-9 ②
k=2
b=-1
{
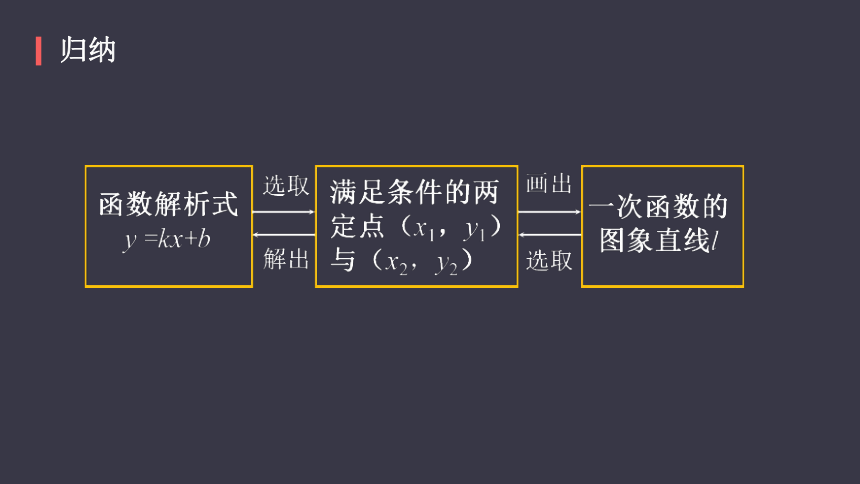
归纳?
用待定系数法求一次函数解析式的一般步骤:
一设:
二代:
三解:
四写:
设解析式为y=kx+b
把点坐标代入解析式,得到两个关于
k和b的方程
联立方程,解出k和b
写出解析式
归纳
练习
已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
设函数解析式为y=kx+b,
将点(9,0)和点(24,20)分别代入y=km+b,得?
? ? ? ? ? ? ? ? ? ? ? ? 解得?
所求的函数解析式为y=x-12??
9k+b=0
24k+b=20
{
k=1
b=-12
{
练习
如图所示,纸箱AB的函数表达式是(? ? )
A
A.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?B.
C.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?D.
练习
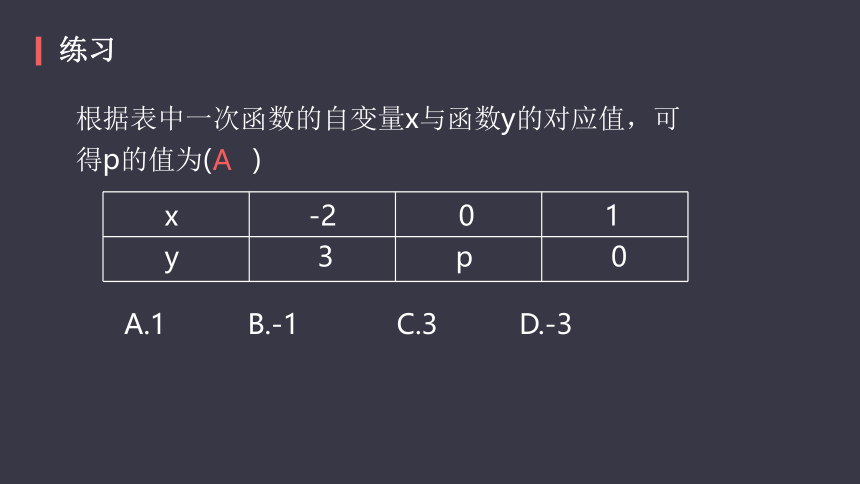
根据表中一次函数的自变量x与函数y的对应值,可
得p的值为(? ? ?)?
A.1? ? ? ? ? B.-1? ? ? ? ? ? C.3? ? ? ? ? D.-3
A
x? ? ? ? ? ? ? ??-2? ? ? ? ? ? ? 0? ? ? ? ? ? ? ? 1
y? ? ? ? ? ? ? ? ?3? ? ? ? ? ? ? p? ? ? ? ? ? ? ? ?0
练习
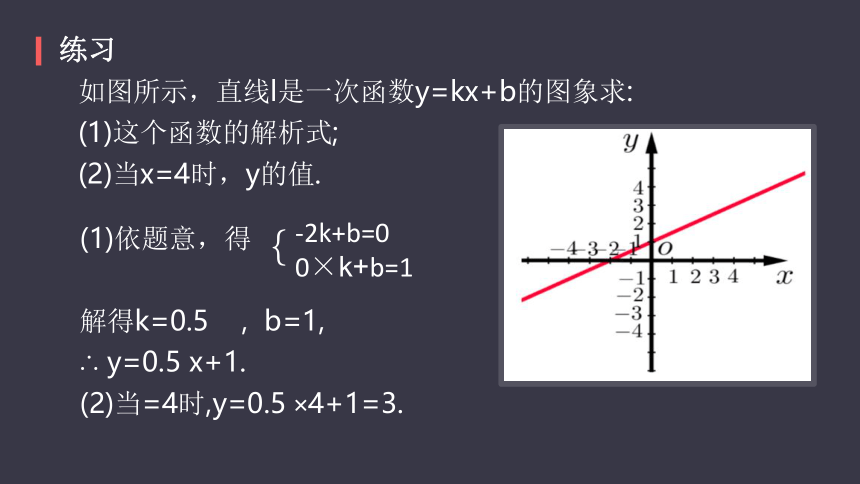
(1)依题意,得
??
解得k=0.5? ? ,? b=1,
∴ y=0.5 x+1.?
(2)当=4时,y=0.5?×4+1=3.?
如图所示,直线l是一次函数y=kx+b的图象求:
(1)这个函数的解析式;
(2)当x=4时,y的值.
-2k+b=0
0×k+b=1
{
补充题
已知:在平面直角坐标系xOy中,一次函数y=kx+4
的图象与轴交于点A,与轴交于点B,OA=2OB
(1)求点A、点B的坐标;
(2)求一次函数的解析式? .
答案:(1)A(0,4)B(2,0)或(2,0);
? ? ? ? ??(2)y=2x+4或y=-2x+4.
例题
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填出下表:
(2)写出付款金额 y(单位:元)与购买种子数量x(单位:kg)之间的函数解析式,并画出函数图象.
例题
(2)设购买量为xkg,付款金额为y元
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2
函数图象如图.
解(1)
思考1 一次购买1.5 kg 种子,需付款多少元?
思考2 一次购买3 kg 种子,需付款多少元?
例题
(2)设购买量为xkg,付款金额为y元
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2
函数图象如图.
解(1)
这种函数叫做分段函数.?
写分段函数时,一定要写清楚每一段的范围.
练习
一个试验室在0:00—2:00保持20℃的恒温,在2:00-4:00匀速升温,每小时升高5℃。写出试验室温度T(单位:℃)关于时间l(单位:h)的函数解析式,并画出函数图象
练习
如图,线段AB是下列哪个函数的图象(? ? ? ? )
A.
B.
C.
D.
D
练习
某图书定价25元,书店规定:如果一次购买此图书20本以上,则超过20本的部分打八折.
(1)写出付款金额y(元)与购书数量x(本)之间的函数关系式?
(2)利用(1)中的函数关系计算:一次购买此图书33本,付款金额是多少元??
补充题
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示.
(1)求第20天的总用水量;
2)当≥20时,求y关于x的函数解析式;
(3)种植时间为多少天时,总用水量达到7000米3??
答案:(1)1000(米? ?)
? ? ? ? ?(2)y=300x-5000
? ? ? ? ?(3)40天.
3
总结
1.用待定系数法求一次函数解析式的一般步骤:
2.写分段函数的解析式时的注意事项:
一设:二代:三解:四 写:?
?
?
要写清楚每一段x对应的范围
一次函数的几何变换
已知直线y=2x-1
(1)求它关于轴对称的直线所对应的函数表式;
(2)将直线y=2x-1向左平移3个单位,求平移后所得直线所对应函数表达式;
(3)将直线y=2x-1绕原点顺时针旋转90°,求旋转后所得直线.
答案:
平行直线k相同
过点(-1,7)的一条直线与x轴、y轴分别相交于点A,B,且与直线y=- x+1平行,求在线段AB上,横、纵坐标都是整数的点的坐标.?
答案:(1,4),(3,1)
一次函数与面积问题
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式. (2)若点C是直线AB在第一象限内的一个点,且△BOC的面积为2,
求点C的坐标。?
答案:(1)直线AB所对应的函数解析?式为y=2x-2;
(2)点C的坐标是(2,2)
一次函数与面积问题
如图,已知直线y=m+3的图象与x轴、y轴分别交于A,B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线L所对应的函数解析式.?
一次函数与面积问题
已知直线y=-+2与轴、y轴分别交于点A和点B,另一直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两部分
(1)若△AOB被分成的两部分面积相等,求k和b的值
(2)若△AOB被分成的两部分面积之比为1求k和b的值??
一次函数与面积问题
如图,在平面直角坐标系中,A(1,0),B(0,1)C(-1,0),过点C的直线1绕点C旋转,交y轴于点D,交线段AB于点E.
(1)求∠OAB的度数及直线AB所对应的函数解析式
(2)若△OCD与△BDE的面积相等,求直线CE所对应的函数解析式.?
复杂的行程问题
甲、乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶设甲、乙两车与B地的距离分别为y? ? (km)y? ? (km),甲车行驶的时间为x(h),y?,y? ?与x之间的函数图像如图所示,结合图象解答下列问题.
(1)乙车休息了_____________
(2)求乙车与甲车相遇后y与x的函数解
析式,并写出自变量的取值范围?
答案:(2)y? ? =80x(2.5≤x≤5)
甲
乙
甲
乙
0.5
乙
复杂的行程问题
甲、乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2b后休息,与甲车相遇后,继续行驶设甲、乙两车与B地的距离分别为y? ?(km)y? ? (km),甲车行驶的时间为x(h),y? ? y? ? 与x之间的函数图像如图所示,结合图象解答下列问题:
?(3)当两车相距40km时,直接写出x的值11??
甲
乙
甲
乙
复杂的行程问题
甲、乙两车分别从A,B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示的是甲、乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数关系图象,其中D点表示甲车到达B地,停止行驶.
(1)A,B两地间的距离为_____________ 千米;
? ? ?乙车的速度是_____________;?
? ? ?a的值为_____________?
560
100千米/时
复杂的行程问题
甲、乙两车分别从A,B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示的是甲、乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数关系图象,其中D点表示甲车到达B地,停止行驶.
(2)乙出发多长时间后两车相距330千米?
答案:(2)0.5小时或35小时
一次函数与几何综合
如图,在平面直角坐标系xOy中,直线y=-? ? ?x+8与x轴,y轴分别交于点A和点B,点D在y轴的负半轴上若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上,落点记为点C.
(1)求AB的长和点C的坐标
(2)求直线CD所对应的函数解析式
答案:(1)AB=10,C(16,0)
教学目标
学会用待定系数法求一次函数解析式.
了解分段函数的表示及其图象,?
能初步应用一次函数模型解决现实生活中的问题,体会一次函数的应用价值.
教学重点
用待定系数法求一次函数解析式.?
初步了解分段函数.
一次函数的应用.
教学难点
思考
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
y=x-1
y=-2x+3
两点法——两点确定一条直线
反过来已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
例题
已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:求一次函数y=kx+b的解析式,关键是求出k,b的值。从已知条件可以列出关于k,b的二元一次方程组,并求出k,b
这种求解析式的方法,
叫做待定系数法.
解:设这个一次函数的解析式为y=kx+b
因为y=kx+b的图象过点(3,5)与(-4,-9),所以 解方程组得 {
这个一次函数的解析式为y=2x-1
3k+b=5 ①
-4k+b=-9 ②
k=2
b=-1
{
归纳?
用待定系数法求一次函数解析式的一般步骤:
一设:
二代:
三解:
四写:
设解析式为y=kx+b
把点坐标代入解析式,得到两个关于
k和b的方程
联立方程,解出k和b
写出解析式
归纳
练习
已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
设函数解析式为y=kx+b,
将点(9,0)和点(24,20)分别代入y=km+b,得?
? ? ? ? ? ? ? ? ? ? ? ? 解得?
所求的函数解析式为y=x-12??
9k+b=0
24k+b=20
{
k=1
b=-12
{
练习
如图所示,纸箱AB的函数表达式是(? ? )
A
A.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?B.
C.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?D.
练习
根据表中一次函数的自变量x与函数y的对应值,可
得p的值为(? ? ?)?
A.1? ? ? ? ? B.-1? ? ? ? ? ? C.3? ? ? ? ? D.-3
A
x? ? ? ? ? ? ? ??-2? ? ? ? ? ? ? 0? ? ? ? ? ? ? ? 1
y? ? ? ? ? ? ? ? ?3? ? ? ? ? ? ? p? ? ? ? ? ? ? ? ?0
练习
(1)依题意,得
??
解得k=0.5? ? ,? b=1,
∴ y=0.5 x+1.?
(2)当=4时,y=0.5?×4+1=3.?
如图所示,直线l是一次函数y=kx+b的图象求:
(1)这个函数的解析式;
(2)当x=4时,y的值.
-2k+b=0
0×k+b=1
{
补充题
已知:在平面直角坐标系xOy中,一次函数y=kx+4
的图象与轴交于点A,与轴交于点B,OA=2OB
(1)求点A、点B的坐标;
(2)求一次函数的解析式? .
答案:(1)A(0,4)B(2,0)或(2,0);
? ? ? ? ??(2)y=2x+4或y=-2x+4.
例题
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填出下表:
(2)写出付款金额 y(单位:元)与购买种子数量x(单位:kg)之间的函数解析式,并画出函数图象.
例题
(2)设购买量为xkg,付款金额为y元
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2
函数图象如图.
解(1)
思考1 一次购买1.5 kg 种子,需付款多少元?
思考2 一次购买3 kg 种子,需付款多少元?
例题
(2)设购买量为xkg,付款金额为y元
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2
函数图象如图.
解(1)
这种函数叫做分段函数.?
写分段函数时,一定要写清楚每一段的范围.
练习
一个试验室在0:00—2:00保持20℃的恒温,在2:00-4:00匀速升温,每小时升高5℃。写出试验室温度T(单位:℃)关于时间l(单位:h)的函数解析式,并画出函数图象
练习
如图,线段AB是下列哪个函数的图象(? ? ? ? )
A.
B.
C.
D.
D
练习
某图书定价25元,书店规定:如果一次购买此图书20本以上,则超过20本的部分打八折.
(1)写出付款金额y(元)与购书数量x(本)之间的函数关系式?
(2)利用(1)中的函数关系计算:一次购买此图书33本,付款金额是多少元??
补充题
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示.
(1)求第20天的总用水量;
2)当≥20时,求y关于x的函数解析式;
(3)种植时间为多少天时,总用水量达到7000米3??
答案:(1)1000(米? ?)
? ? ? ? ?(2)y=300x-5000
? ? ? ? ?(3)40天.
3
总结
1.用待定系数法求一次函数解析式的一般步骤:
2.写分段函数的解析式时的注意事项:
一设:二代:三解:四 写:?
?
?
要写清楚每一段x对应的范围
一次函数的几何变换
已知直线y=2x-1
(1)求它关于轴对称的直线所对应的函数表式;
(2)将直线y=2x-1向左平移3个单位,求平移后所得直线所对应函数表达式;
(3)将直线y=2x-1绕原点顺时针旋转90°,求旋转后所得直线.
答案:
平行直线k相同
过点(-1,7)的一条直线与x轴、y轴分别相交于点A,B,且与直线y=- x+1平行,求在线段AB上,横、纵坐标都是整数的点的坐标.?
答案:(1,4),(3,1)
一次函数与面积问题
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式. (2)若点C是直线AB在第一象限内的一个点,且△BOC的面积为2,
求点C的坐标。?
答案:(1)直线AB所对应的函数解析?式为y=2x-2;
(2)点C的坐标是(2,2)
一次函数与面积问题
如图,已知直线y=m+3的图象与x轴、y轴分别交于A,B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线L所对应的函数解析式.?
一次函数与面积问题
已知直线y=-+2与轴、y轴分别交于点A和点B,另一直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两部分
(1)若△AOB被分成的两部分面积相等,求k和b的值
(2)若△AOB被分成的两部分面积之比为1求k和b的值??
一次函数与面积问题
如图,在平面直角坐标系中,A(1,0),B(0,1)C(-1,0),过点C的直线1绕点C旋转,交y轴于点D,交线段AB于点E.
(1)求∠OAB的度数及直线AB所对应的函数解析式
(2)若△OCD与△BDE的面积相等,求直线CE所对应的函数解析式.?
复杂的行程问题
甲、乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶设甲、乙两车与B地的距离分别为y? ? (km)y? ? (km),甲车行驶的时间为x(h),y?,y? ?与x之间的函数图像如图所示,结合图象解答下列问题.
(1)乙车休息了_____________
(2)求乙车与甲车相遇后y与x的函数解
析式,并写出自变量的取值范围?
答案:(2)y? ? =80x(2.5≤x≤5)
甲
乙
甲
乙
0.5
乙
复杂的行程问题
甲、乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2b后休息,与甲车相遇后,继续行驶设甲、乙两车与B地的距离分别为y? ?(km)y? ? (km),甲车行驶的时间为x(h),y? ? y? ? 与x之间的函数图像如图所示,结合图象解答下列问题:
?(3)当两车相距40km时,直接写出x的值11??
甲
乙
甲
乙
复杂的行程问题
甲、乙两车分别从A,B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示的是甲、乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数关系图象,其中D点表示甲车到达B地,停止行驶.
(1)A,B两地间的距离为_____________ 千米;
? ? ?乙车的速度是_____________;?
? ? ?a的值为_____________?
560
100千米/时
复杂的行程问题
甲、乙两车分别从A,B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示的是甲、乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数关系图象,其中D点表示甲车到达B地,停止行驶.
(2)乙出发多长时间后两车相距330千米?
答案:(2)0.5小时或35小时
一次函数与几何综合
如图,在平面直角坐标系xOy中,直线y=-? ? ?x+8与x轴,y轴分别交于点A和点B,点D在y轴的负半轴上若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上,落点记为点C.
(1)求AB的长和点C的坐标
(2)求直线CD所对应的函数解析式
答案:(1)AB=10,C(16,0)
