人教版八年级数学下册第十九章:19.3课题学习 选择方案 课件(共48张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十九章:19.3课题学习 选择方案 课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 947.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






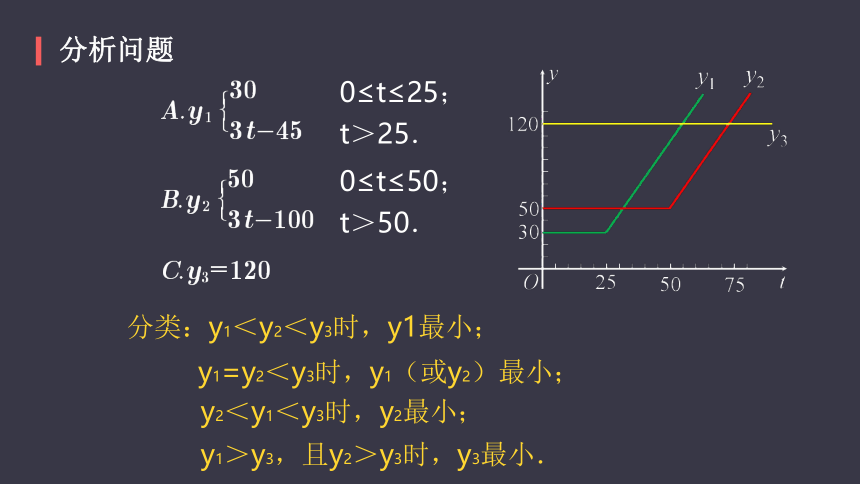


文档简介
课题学习 选择方案
教学目标
会用一次函数知识解决方案选择问题,体会函数模型思想.?
能从不同的角度思考问题,优化解决问题的方法.
能进行解决问题过程的反思,总结解决问题的方法.
教学重点
教学难点
建立函数模型解决方案选择问题.
应用一次函数模型解决方案选择问题.
提出问题
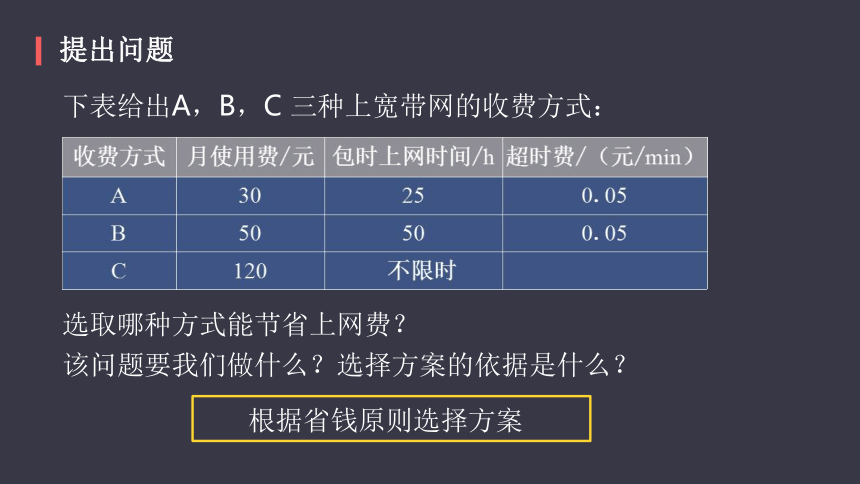
下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
根据省钱原则选择方案
分析问题
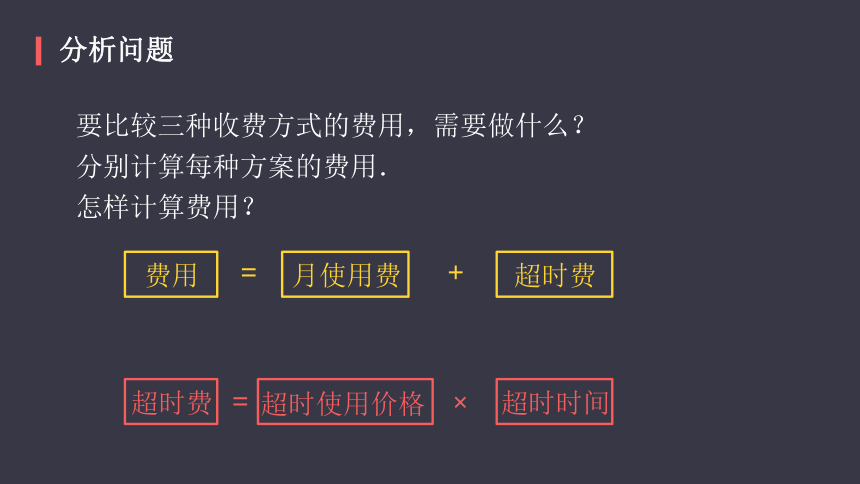
要比较三种收费方式的费用,需要做什么?
分别计算每种方案的费用.
怎样计算费用?
费用
月使用费
超时费
超时费
超时使用价格?
超时时间
=? ? ? ? ? ? ? ? ? ? ? ?+
=? ? ? ? ? ? ? ? ? ? ? ? ?×
A,B,C 三种方案中,所需要的费用是固定的还是变化的?
方案C费用固定;
方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.
分析问题
分析问题
请分别写出三种方案的上网费用y 元与上网时间t h
之间的函数解析式.
方案A费用:
方案B费用:
方案C费用:
0≤t≤25;
t>25.
0≤t≤50;
t>50.
分析问题
能把这个问题描述为函数问题吗?
设上网时间为 t,方案A,B,C的上网费用分别为y1 元,y2 元, y3 元,且
0≤t≤25;
t>25.
0≤t≤50;
t>50.
请比较? ? ? ? ? ? ? 的大小.
这个问题看起来还是有点复杂,难点在于每一个函数的解析都是分类表示的,需要分类讨论,而怎样分类是难点.怎么办?
——先画出图象看看.
分析问题
0≤t≤25;
t>25.
0≤t≤50;
t>50.
分类:y1<y2<y3时,y1最小;
y1=y2<y3时,y1(或y2)最小;
y2<y1<y3时,y2最小;
y1>y3,且y2>y3时,y3最小.
解决问题
解:设上网时间为t h,方案A,B,C的上网费用分别为y1元,y2元, y3元,则
0≤t≤25;
t>25.
0≤t≤50;
t>50.
结合图象可知:
(1)若y1=y2,即3t-45=50,解方程,得t =31小时40分 ;
(2)若y1<y2,即3t-45<50,解不等式,得t<31小时40分 ;
(3)若y1>y2,即3t-45>50,解不等式,得t>31小时40分 .
解决问题
解:令3t-100=120,解方程,得t =73小时20分? ? ?;
令3t-100>120,解不等式,得t>73小时20分 .
当上网时间不超过31小时40分,选择方案A最省钱;
当上网时间为31小时40分至73小时20分,选择方案B最省钱;??
当上网时间超过73小时20分,选择方案C最省钱.
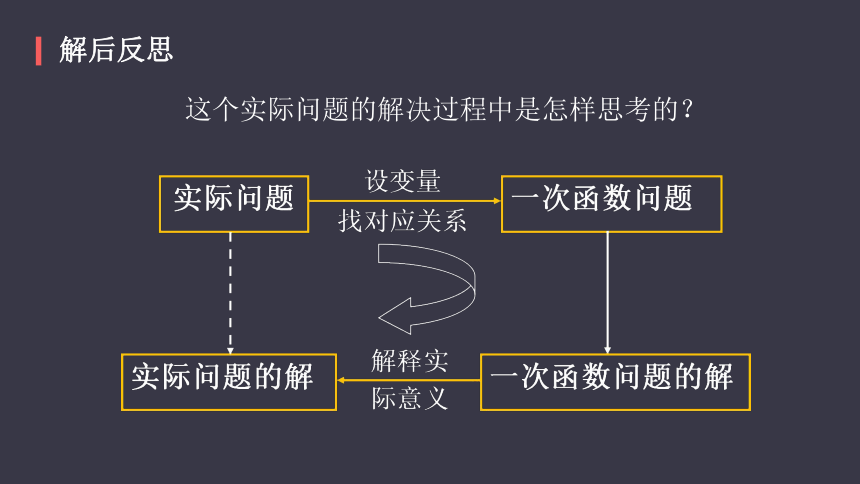
解后反思
这个实际问题的解决过程中是怎样思考的?
提出问题
某学校计划在总费用2 300 元的限额内,租用汽车送234 名学生和6 名教师集体外出活动,每辆汽车上至少要有1 名教师.现在有甲、乙两种大客车,它们的载客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
分析问题
问题1 影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
问题2 汽车所租辆数又与哪些因素有关?
与乘车人数有关.
问题3 如何由乘车人数确定租车辆数呢?
(1)要保证240 名师生都有车坐,汽车总数不能小于6 辆;
(2)要使每辆汽车上至少有1 名教师,汽车总数不能大于6 辆.
分析问题
在汽车总数确定后,租车费用与租车的种类有关.如果租甲类车x 辆,能求出租车费用吗?
设租用 x 辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;设租车费用为 y,则
? ? ? ? ? ? ? ? ? ? ? ? ??
y =400x+280(6-x)
化简 得??
y =120x+1 680.
分析问题
如何确定 y =120x+1 680中 y 的最小值.
(1)为使240 名师生有车坐,则45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则 400x+280(6-x)≤2 300.
由 得 4≤x≤5 .
据实际意义可取4 或5; ?
因为 y 随着 x 的增大而增大,所以当 x =4 时,y 最小,y 的最小值为2 160.
45X+30(6-X)≥240
400X+280(6-X)≤2300
解决问题
解:设租用x 辆甲种客车,则租用乙种客车的辆数为(6-x)辆;设租车费用为 y,则 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
由 45x+30(6-x)≥240;
400x+280(6-x)≤2 300. 得 4≤x≤5 .
? ? (2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
y =400x+280(6-x)
化简 得 y =120x+1 680.
(1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
解决问题
解:据实际意义可取4 或5;
因为 y 随着 x 的增大而增大,
所以当 x =4 时,y 最小,y 的最小值为2 160.
提出问题
灯具店老板介绍说:
一种节能灯的功率是10瓦(即0.01千瓦),售价60元;一种白炽灯的功率是60瓦(即0.06千瓦),售价为3元.两种灯的照明效果是一样的,使用寿命也相同(3000小时以上).? 父亲说:“买白炽灯可以省钱”.而小刚正好读八年级,他在心里默算了一下说:“还是买节能灯吧”.父子二人争执不下.本地电费为0.5元/千瓦.时,请聪明的你帮助他们选择哪一种灯可以省钱呢?
分析问题
题中谈到几种灯?小明准备买几种灯?
两种灯.小明准备买一种灯.
灯的总费用由哪几部分组成?
灯的总费用=灯的售价+电费
电费=0.5×灯的功率(千瓦)×照明时间(时)
分析问题
如何计算两种灯的费用?
设照明时间是x小时, 节能灯的费用y1元表示,
白炽灯的费用y2元表示,则有:
y1=60+0.5×0.01x=0.005x+60;
y2=3+0.5×0.06x=0.03x+3.
分析问题
观察上述两个函数
(1)若使用两种灯的费用相等,它的含义是什么?
(2)若使用节能灯省钱,它的含义是什么?
(3)若使用白炽灯省钱,它的含义是什么?
y1=y2??? ? ?即:x取,何值时y1=y2????
y1<y2??? ? ?即:x取,何值时y1?<y2????
y1?>y2??? ? ?即:x取,何值时y1?>y2????
解决问题
从“数”上解
y1=60+0.5×0.01x=0.005x+60;?
y2=3+0.5×0.06x=0.03x+3.
y1=y2
0.005x×60=0.03x+33
解得:x=2280
即当照明时间等于2280小时,购买节能灯、白炽灯均可.
解决问题
从“数”上解
若y1<y2 ,则有0.005x+60<0.03x+3
解得:x>2280
即当照明时间大于2280小时,购买节能灯较省钱.
若y1?>y2 ,则有0.005x+60<0.03x+3
解得:x<2280
即当照明时间小于2280小时,购买白炽灯较省钱.
解决问题
从“形”上解
解:设照明时间是x小时, 节能灯的费用用y1元表示,白炽灯的费用用y2元表示,则有:
y1=0.005x+60;
y2=0.003x+3
解决问题
从“形”上解
由图象可知:
当x=2280时, y1= y2,
故照明时间等于2280小时,
购买节能灯、白炽灯均可.
解决问题
从“形”上解
当x>2280时, y1< y2,
故照明时间大于2280小时,
且不超过3000小时,用节能灯
省钱;
?
解决问题
从“形”上解
当x<2280时, y1> y2,
故照明时间小于2280时,
用白炽灯省钱.
提出问题
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小.
分析问题
设从A水库调往甲地的水量为x吨,则有
14-x? ? ? ? ? ? ? ?
x-1?
15-x
15? ? ? ? ? ? ? ?13? ? ? ? ? ? ? ? 28?
14?
14?
解决问题
设从A水库调往甲地的水量为x万吨 ,总调运量为y万吨则
从A水库调往乙地的水量为(14-x)万吨
从B水库调往甲地的水量为(15-x)万吨
从B水库调往乙地的水量为(x-1)万吨
y=50x+30(14-x)+60(15-x)+45(x-1)
解决问题
y=50x+30(14-x)+60(15-x)+45(x-1)
(1)化简这个函数,并指出其中自变量x的取值应有什么限制条件?
y=5x+1275
x应满足 15-x≥0 14-x≥0 x-1≥0
∴1≤x≤14
解决问题
(2)画出这个函数的图象
解决问题
(3)结合函数解析式及其图像说明水的最佳调运方案.水的最小调运量为多少?
y = 5x +1275的值 y随x 的增大
而增大,所以当x=1时y 有最小值,最小值为5×1+1275=1280,
所以运水方案
从A地调往甲地1万吨,
从A地调往乙地14-1=13(万吨);
从B地调往甲地15-1=14(万吨),
从B地调往乙地1-1=0(万吨)
复习巩固
1.小亮现已存款100元,为赞助“希望工程”,
他计划今后三年每月存款10元。存款总金
额y(单位:元)将随时间x(单位:月)
的变化而改变。指出其中的常量与变量,
自变量与函数,并写出函数解析式
复习巩固
2.判断下列各点是否在直线y=2x+6上.
这条直线与坐标轴交于何处?
(-5,-4),(-7,20)
复习巩固
3.填空
(1)直线y=? ? ? ? ?x经过第________ 象限,y随x的增大而________ ;
(2)直线y=3x-2经过第________??象限,y随x的增大而________.?
复习巩固
4.根据下列条件分别确定函数y=kx+b的解析式:
(1)y与x成正比例,当x=5时,y=6;
(2)直线y=kx+b经过点(3,6)与点
复习巩固
5.试根据函数y=3x-15的性质或图象,确定x取何值时:
(1)y>0;? ? ? ? ? ? ? ? ? ? ? ?(2)y<0
综合运用
6.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元。设托运kg(p为整数)物品的费用为c元。试写出c的计算公式.
综合运用
7. 某水果批发市场规定,批发苹果不少于100kg时,批发价为2.5元/kg。小王携带现金3000元到这市场采购苹果,并以批发价买进。设购买的苹果为xkg,小王付款后还剩余现金y元,试写出y关于x的函数解析式,并指出自变量x的取值范围
综合运用
8.匀速地向一个容器内注水,最后把容器注满。在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线)。这个容器的形状是下图中哪一个?匀速地向另两个容器注水时,你能画出水面高度h随时间t变化的图象(草图)吗?
综合运用
9.已知等腰三角形周长为20
(1)写出底边长y关于腰长x的函数解析式(x为自变量);
(2)写出自变量取值范围;
(3)在直角坐标系中,画出函数图象
综合运用
10.已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10。设△OPA的面积为S.
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=12时,求P点坐标;
(4)画出函数S的图象
综合运用
11. (1)画出函数y=|x-1|的图象??
? ? ? (2)设P(x,0)是x轴上的一个动点,它与x轴上表示一3的点的距离为y.
? ? ? ?求y关于x的函数解析式,并画出这个函数的图象
综合运用
12.A,B两地相距25km。甲8:00由A地出发骑自行车去B地,平均速度为10km/h;乙9:30由A地出发乘汽车也去B地,平均速度为40km/h。
(1)分别写出两个人的行程关于时刻的函数解析式.
(2)乙能否在途中超过甲?如果能超过,何时超过?
拓广探索
14.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m。此后两人分别以am/s和bm/s匀速跑。又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点,这次越野赛跑的全程为多少米?
拓广探索
15.A城有肥料200t,B城有肥料300t。现要把这些肥料全部运往C,D两乡。从A城往C,D两乡运肥料的费用分别为20元/t和25元/t;从B城往C,D两乡运肥料的费用分别为15元/t和24元/t。现C乡需要肥料240t,D乡需要肥料260t,怎样调运可使总运费最少?
教学目标
会用一次函数知识解决方案选择问题,体会函数模型思想.?
能从不同的角度思考问题,优化解决问题的方法.
能进行解决问题过程的反思,总结解决问题的方法.
教学重点
教学难点
建立函数模型解决方案选择问题.
应用一次函数模型解决方案选择问题.
提出问题
下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
根据省钱原则选择方案
分析问题
要比较三种收费方式的费用,需要做什么?
分别计算每种方案的费用.
怎样计算费用?
费用
月使用费
超时费
超时费
超时使用价格?
超时时间
=? ? ? ? ? ? ? ? ? ? ? ?+
=? ? ? ? ? ? ? ? ? ? ? ? ?×
A,B,C 三种方案中,所需要的费用是固定的还是变化的?
方案C费用固定;
方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.
分析问题
分析问题
请分别写出三种方案的上网费用y 元与上网时间t h
之间的函数解析式.
方案A费用:
方案B费用:
方案C费用:
0≤t≤25;
t>25.
0≤t≤50;
t>50.
分析问题
能把这个问题描述为函数问题吗?
设上网时间为 t,方案A,B,C的上网费用分别为y1 元,y2 元, y3 元,且
0≤t≤25;
t>25.
0≤t≤50;
t>50.
请比较? ? ? ? ? ? ? 的大小.
这个问题看起来还是有点复杂,难点在于每一个函数的解析都是分类表示的,需要分类讨论,而怎样分类是难点.怎么办?
——先画出图象看看.
分析问题
0≤t≤25;
t>25.
0≤t≤50;
t>50.
分类:y1<y2<y3时,y1最小;
y1=y2<y3时,y1(或y2)最小;
y2<y1<y3时,y2最小;
y1>y3,且y2>y3时,y3最小.
解决问题
解:设上网时间为t h,方案A,B,C的上网费用分别为y1元,y2元, y3元,则
0≤t≤25;
t>25.
0≤t≤50;
t>50.
结合图象可知:
(1)若y1=y2,即3t-45=50,解方程,得t =31小时40分 ;
(2)若y1<y2,即3t-45<50,解不等式,得t<31小时40分 ;
(3)若y1>y2,即3t-45>50,解不等式,得t>31小时40分 .
解决问题
解:令3t-100=120,解方程,得t =73小时20分? ? ?;
令3t-100>120,解不等式,得t>73小时20分 .
当上网时间不超过31小时40分,选择方案A最省钱;
当上网时间为31小时40分至73小时20分,选择方案B最省钱;??
当上网时间超过73小时20分,选择方案C最省钱.
解后反思
这个实际问题的解决过程中是怎样思考的?
提出问题
某学校计划在总费用2 300 元的限额内,租用汽车送234 名学生和6 名教师集体外出活动,每辆汽车上至少要有1 名教师.现在有甲、乙两种大客车,它们的载客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
分析问题
问题1 影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
问题2 汽车所租辆数又与哪些因素有关?
与乘车人数有关.
问题3 如何由乘车人数确定租车辆数呢?
(1)要保证240 名师生都有车坐,汽车总数不能小于6 辆;
(2)要使每辆汽车上至少有1 名教师,汽车总数不能大于6 辆.
分析问题
在汽车总数确定后,租车费用与租车的种类有关.如果租甲类车x 辆,能求出租车费用吗?
设租用 x 辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;设租车费用为 y,则
? ? ? ? ? ? ? ? ? ? ? ? ??
y =400x+280(6-x)
化简 得??
y =120x+1 680.
分析问题
如何确定 y =120x+1 680中 y 的最小值.
(1)为使240 名师生有车坐,则45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则 400x+280(6-x)≤2 300.
由 得 4≤x≤5 .
据实际意义可取4 或5; ?
因为 y 随着 x 的增大而增大,所以当 x =4 时,y 最小,y 的最小值为2 160.
45X+30(6-X)≥240
400X+280(6-X)≤2300
解决问题
解:设租用x 辆甲种客车,则租用乙种客车的辆数为(6-x)辆;设租车费用为 y,则 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
由 45x+30(6-x)≥240;
400x+280(6-x)≤2 300. 得 4≤x≤5 .
? ? (2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300.
y =400x+280(6-x)
化简 得 y =120x+1 680.
(1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
解决问题
解:据实际意义可取4 或5;
因为 y 随着 x 的增大而增大,
所以当 x =4 时,y 最小,y 的最小值为2 160.
提出问题
灯具店老板介绍说:
一种节能灯的功率是10瓦(即0.01千瓦),售价60元;一种白炽灯的功率是60瓦(即0.06千瓦),售价为3元.两种灯的照明效果是一样的,使用寿命也相同(3000小时以上).? 父亲说:“买白炽灯可以省钱”.而小刚正好读八年级,他在心里默算了一下说:“还是买节能灯吧”.父子二人争执不下.本地电费为0.5元/千瓦.时,请聪明的你帮助他们选择哪一种灯可以省钱呢?
分析问题
题中谈到几种灯?小明准备买几种灯?
两种灯.小明准备买一种灯.
灯的总费用由哪几部分组成?
灯的总费用=灯的售价+电费
电费=0.5×灯的功率(千瓦)×照明时间(时)
分析问题
如何计算两种灯的费用?
设照明时间是x小时, 节能灯的费用y1元表示,
白炽灯的费用y2元表示,则有:
y1=60+0.5×0.01x=0.005x+60;
y2=3+0.5×0.06x=0.03x+3.
分析问题
观察上述两个函数
(1)若使用两种灯的费用相等,它的含义是什么?
(2)若使用节能灯省钱,它的含义是什么?
(3)若使用白炽灯省钱,它的含义是什么?
y1=y2??? ? ?即:x取,何值时y1=y2????
y1<y2??? ? ?即:x取,何值时y1?<y2????
y1?>y2??? ? ?即:x取,何值时y1?>y2????
解决问题
从“数”上解
y1=60+0.5×0.01x=0.005x+60;?
y2=3+0.5×0.06x=0.03x+3.
y1=y2
0.005x×60=0.03x+33
解得:x=2280
即当照明时间等于2280小时,购买节能灯、白炽灯均可.
解决问题
从“数”上解
若y1<y2 ,则有0.005x+60<0.03x+3
解得:x>2280
即当照明时间大于2280小时,购买节能灯较省钱.
若y1?>y2 ,则有0.005x+60<0.03x+3
解得:x<2280
即当照明时间小于2280小时,购买白炽灯较省钱.
解决问题
从“形”上解
解:设照明时间是x小时, 节能灯的费用用y1元表示,白炽灯的费用用y2元表示,则有:
y1=0.005x+60;
y2=0.003x+3
解决问题
从“形”上解
由图象可知:
当x=2280时, y1= y2,
故照明时间等于2280小时,
购买节能灯、白炽灯均可.
解决问题
从“形”上解
当x>2280时, y1< y2,
故照明时间大于2280小时,
且不超过3000小时,用节能灯
省钱;
?
解决问题
从“形”上解
当x<2280时, y1> y2,
故照明时间小于2280时,
用白炽灯省钱.
提出问题
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小.
分析问题
设从A水库调往甲地的水量为x吨,则有
14-x? ? ? ? ? ? ? ?
x-1?
15-x
15? ? ? ? ? ? ? ?13? ? ? ? ? ? ? ? 28?
14?
14?
解决问题
设从A水库调往甲地的水量为x万吨 ,总调运量为y万吨则
从A水库调往乙地的水量为(14-x)万吨
从B水库调往甲地的水量为(15-x)万吨
从B水库调往乙地的水量为(x-1)万吨
y=50x+30(14-x)+60(15-x)+45(x-1)
解决问题
y=50x+30(14-x)+60(15-x)+45(x-1)
(1)化简这个函数,并指出其中自变量x的取值应有什么限制条件?
y=5x+1275
x应满足 15-x≥0 14-x≥0 x-1≥0
∴1≤x≤14
解决问题
(2)画出这个函数的图象
解决问题
(3)结合函数解析式及其图像说明水的最佳调运方案.水的最小调运量为多少?
y = 5x +1275的值 y随x 的增大
而增大,所以当x=1时y 有最小值,最小值为5×1+1275=1280,
所以运水方案
从A地调往甲地1万吨,
从A地调往乙地14-1=13(万吨);
从B地调往甲地15-1=14(万吨),
从B地调往乙地1-1=0(万吨)
复习巩固
1.小亮现已存款100元,为赞助“希望工程”,
他计划今后三年每月存款10元。存款总金
额y(单位:元)将随时间x(单位:月)
的变化而改变。指出其中的常量与变量,
自变量与函数,并写出函数解析式
复习巩固
2.判断下列各点是否在直线y=2x+6上.
这条直线与坐标轴交于何处?
(-5,-4),(-7,20)
复习巩固
3.填空
(1)直线y=? ? ? ? ?x经过第________ 象限,y随x的增大而________ ;
(2)直线y=3x-2经过第________??象限,y随x的增大而________.?
复习巩固
4.根据下列条件分别确定函数y=kx+b的解析式:
(1)y与x成正比例,当x=5时,y=6;
(2)直线y=kx+b经过点(3,6)与点
复习巩固
5.试根据函数y=3x-15的性质或图象,确定x取何值时:
(1)y>0;? ? ? ? ? ? ? ? ? ? ? ?(2)y<0
综合运用
6.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元。设托运kg(p为整数)物品的费用为c元。试写出c的计算公式.
综合运用
7. 某水果批发市场规定,批发苹果不少于100kg时,批发价为2.5元/kg。小王携带现金3000元到这市场采购苹果,并以批发价买进。设购买的苹果为xkg,小王付款后还剩余现金y元,试写出y关于x的函数解析式,并指出自变量x的取值范围
综合运用
8.匀速地向一个容器内注水,最后把容器注满。在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线)。这个容器的形状是下图中哪一个?匀速地向另两个容器注水时,你能画出水面高度h随时间t变化的图象(草图)吗?
综合运用
9.已知等腰三角形周长为20
(1)写出底边长y关于腰长x的函数解析式(x为自变量);
(2)写出自变量取值范围;
(3)在直角坐标系中,画出函数图象
综合运用
10.已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10。设△OPA的面积为S.
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=12时,求P点坐标;
(4)画出函数S的图象
综合运用
11. (1)画出函数y=|x-1|的图象??
? ? ? (2)设P(x,0)是x轴上的一个动点,它与x轴上表示一3的点的距离为y.
? ? ? ?求y关于x的函数解析式,并画出这个函数的图象
综合运用
12.A,B两地相距25km。甲8:00由A地出发骑自行车去B地,平均速度为10km/h;乙9:30由A地出发乘汽车也去B地,平均速度为40km/h。
(1)分别写出两个人的行程关于时刻的函数解析式.
(2)乙能否在途中超过甲?如果能超过,何时超过?
拓广探索
14.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m。此后两人分别以am/s和bm/s匀速跑。又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点,这次越野赛跑的全程为多少米?
拓广探索
15.A城有肥料200t,B城有肥料300t。现要把这些肥料全部运往C,D两乡。从A城往C,D两乡运肥料的费用分别为20元/t和25元/t;从B城往C,D两乡运肥料的费用分别为15元/t和24元/t。现C乡需要肥料240t,D乡需要肥料260t,怎样调运可使总运费最少?
