人教版八年级数学下册第十七章:17.1.1勾股定理及证明 课件(共38张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十七章:17.1.1勾股定理及证明 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:41:59 | ||
图片预览









文档简介
勾股定理及证明
教学目标
经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,通过对于我国古代研究勾股定理的成就的介绍,培养学生的民族自豪感.
能用勾股定理解决一些简单问题.
教学重点
教学难点
探索并证明勾股定理.
?
勾股定理的证明.
知识引入
创设情境 引入课题
国际数学家大会是最高水平的全球性数学科学学术会议.
2002年在北京召开了第24届国际数学家大会.如图就是大会的会徽的图案.
?
你见过这个图案吗?
它由哪些基本图形组成?
?
知识引入
创设情境 引入课题
相传2500多年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.我们也来观察一下地面的图案,看看能从中发现什么数量关系?
?
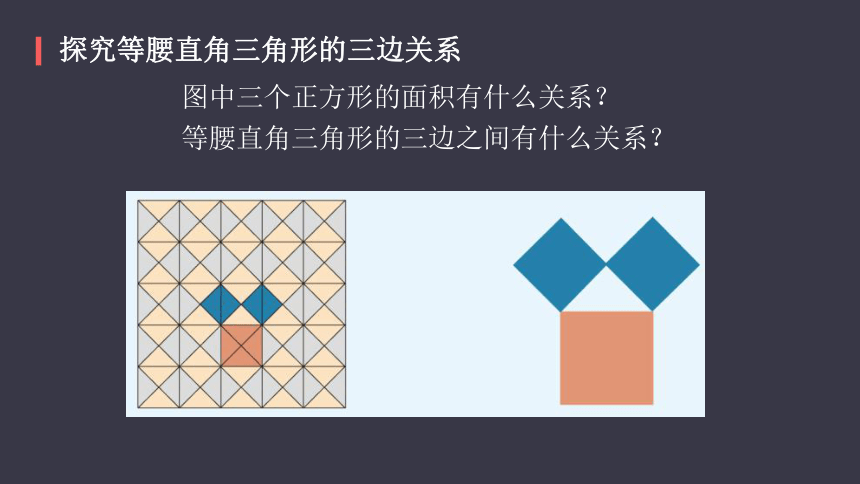
探究等腰直角三角形的三边关系
图中三个正方形的面积有什么关系?
等腰直角三角形的三边之间有什么关系?
?
发现
大正方形的面积=两个小正方形的面积之和
等腰直角三角形的三边之间有一种特殊关系:
斜边的平方等于两直角边的平方和
这是等腰直角三角形特有的性质吗?
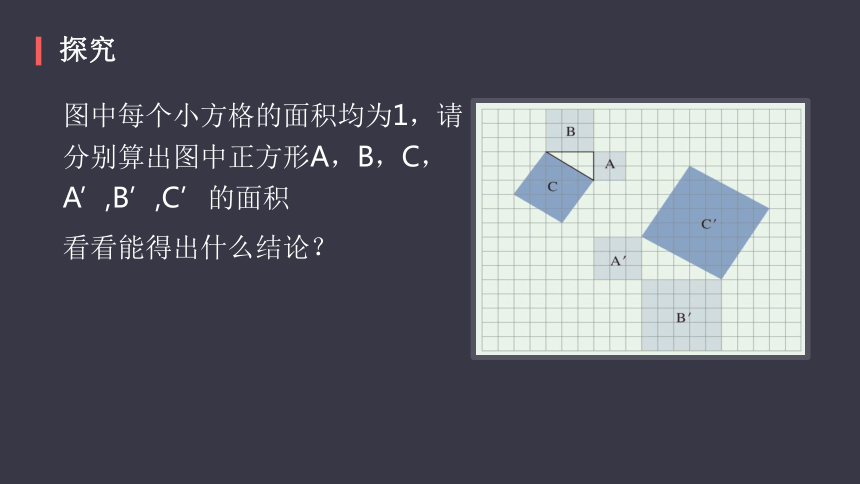
探究
图中每个小方格的面积均为1,请分别算出图中正方形A,B,C,A’,B’,C’的面积
看看能得出什么结论?
猜想
如果直角三角形的两条直角边长分别为a,b,斜边长为c,
那么a,b,c会满足什么关系?
勾股定理
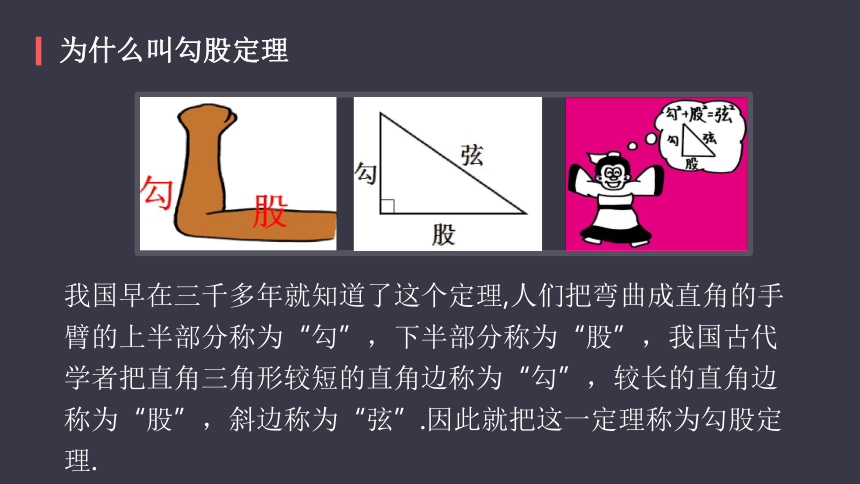
为什么叫勾股定理?
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾股定理的历史
古巴比仑人在公元前19世纪发现就发现了勾股定理.
勾股定理的历史
公元前11世纪,周公与商高的对话(记录于公元前1世纪《周髀算经》)中提出“勾三、股四、弦五”.? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ——勾股定理、商高定理
勾股定理的历史
公元前600年左右,古希腊的毕达哥拉斯学派发现勾股定理,命名为“毕达哥拉斯定理” ,而且给出了证明.为此,他们还杀了一百头牛来庆祝,所以这个定理又叫百牛定理.
勾股定理的历史
这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).?
勾股定理在数学发展中起到了重大的作用,其证明方法据说有400 多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.
赵爽证法
毕达哥拉斯证法
加菲尔德证法
欧几里得证法
例题
求下列直角三角形中未知边的长度.
例题
求图中字母所代表的正方形的面积.
练习
1.设直角三角形的两条直角边长分别为a和b,斜边长为c。
(1)已知a=6,c=10,求b:
(1)已知a=5,b=12,求c:
(1)已知c=6,b=15,求a:
练习
如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
勾股树
练习
在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
⑶ 若 c=17,a=8,则b=____
5
12
15
补充题
在Rt△ABC∠C=90°,BC:AC=3:4,AB=10,
则AC=_____?,BC=_____?
?
8
6
总结
1.勾股定理:
2.勾股的各种证明方法.
特殊三角形的相关计算
如图,在Rt△ABC中,∠C=90°, ∠B=45°,AC=1,则AB=(? ? ? ? ? )
A.2? ? ? ? ? B.1? ? ? ? ? ?C.? ? ? ? ? ? ? ?D.3
C
特殊三角形的相关计算
等边三角形的边长为12,则它的高为______
?
已知直角三角形两边求第三边
在直角三角形中,如果有两边为3,4,那么另一边为_________
勾股定理究竟是谁先发现的??
在西方人们认为勾股定理是毕达哥拉斯先发现的,并称之为“毕达哥拉斯定理”.?
不过早在公元前1120年左右中国的商高就在对话中说到:“故折矩,此为勾广三,股修四,经隅五.”?
你可能认为这是最早的勾股定理,但是具调查在公元前1900年的一块巴比伦上午泥板中,记载了15组勾股数. 所以古巴比伦人才是勾股定理最先的发现人.
勾股定理的来历
中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:
周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?”?
商高回答说:“数的产生来源于对方和圆这些形体饿认识.其中有一条原理:当直角三角形‘矩’得到的一条直角‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜‘弦’就必定是5.这个原理是大禹在治水的时候就总结出来的呵.”
商高定理
商高是公元前十一世纪的中国人.当时中国的朝代是西周,是奴隶社会时期.在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话.商高说:“…故折矩,勾广三,股修四,经隅五.”什么是“勾、股”呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫作"商高定理".
毕达哥拉斯简介
毕达哥拉斯出生于萨摩斯岛,自幼聪明好学,曾在名师门下学习几何,自然学和哲学.后来来到巴比伦,印度和埃及,吸收了阿拉伯文明和印度文明甚至中国文明的丰富营养.
大约在公元前530年,又返回萨摩斯岛,后来又迁居意大利的克罗通,创建了自己的学术.毕达哥拉斯学术认为数最崇高,最神秘,他们所讲的是整数.
可惜,朝气蓬勃的毕达哥拉斯到了晚年不仅学术保守,还反对新生事物,最后死与非命.
毕达哥拉斯定理
毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形磁砖,但毕达哥拉斯不只是欣赏磁砖的美丽,而是想到它们和[数]之间的关系,于是 拿了画笔并且蹲在地板上,选了一块磁砖以它的对角线 AB为边画一个正方形,他发现这个正方形面积恰好等于两块磁砖的面积和.他很好奇.... 于是再以两块磁砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块磁砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设: 任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.
百牛定理
希腊的著明数学家毕达格拉斯发现了这个定理,因此世界上许多国家都称勾股定理为“毕达格拉斯”定理.为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”.
总统与勾股定理
一个周末的傍晚,伽菲尔德突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形.于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀.”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心理很不是滋味.
总统与勾股定理
于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题.他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1881年,伽菲尔德就任美国第二十任总统后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法.
达芬奇与勾股定理
意大利文艺复兴时代的著名画家达芬奇也深深的沉醉在勾股定理的魅力中.
教学目标
经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,通过对于我国古代研究勾股定理的成就的介绍,培养学生的民族自豪感.
能用勾股定理解决一些简单问题.
教学重点
教学难点
探索并证明勾股定理.
?
勾股定理的证明.
知识引入
创设情境 引入课题
国际数学家大会是最高水平的全球性数学科学学术会议.
2002年在北京召开了第24届国际数学家大会.如图就是大会的会徽的图案.
?
你见过这个图案吗?
它由哪些基本图形组成?
?
知识引入
创设情境 引入课题
相传2500多年前,毕达哥拉斯有一次在朋友家作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.我们也来观察一下地面的图案,看看能从中发现什么数量关系?
?
探究等腰直角三角形的三边关系
图中三个正方形的面积有什么关系?
等腰直角三角形的三边之间有什么关系?
?
发现
大正方形的面积=两个小正方形的面积之和
等腰直角三角形的三边之间有一种特殊关系:
斜边的平方等于两直角边的平方和
这是等腰直角三角形特有的性质吗?
探究
图中每个小方格的面积均为1,请分别算出图中正方形A,B,C,A’,B’,C’的面积
看看能得出什么结论?
猜想
如果直角三角形的两条直角边长分别为a,b,斜边长为c,
那么a,b,c会满足什么关系?
勾股定理
为什么叫勾股定理?
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾股定理的历史
古巴比仑人在公元前19世纪发现就发现了勾股定理.
勾股定理的历史
公元前11世纪,周公与商高的对话(记录于公元前1世纪《周髀算经》)中提出“勾三、股四、弦五”.? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ——勾股定理、商高定理
勾股定理的历史
公元前600年左右,古希腊的毕达哥拉斯学派发现勾股定理,命名为“毕达哥拉斯定理” ,而且给出了证明.为此,他们还杀了一百头牛来庆祝,所以这个定理又叫百牛定理.
勾股定理的历史
这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形 (黄色).?
勾股定理在数学发展中起到了重大的作用,其证明方法据说有400 多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.
赵爽证法
毕达哥拉斯证法
加菲尔德证法
欧几里得证法
例题
求下列直角三角形中未知边的长度.
例题
求图中字母所代表的正方形的面积.
练习
1.设直角三角形的两条直角边长分别为a和b,斜边长为c。
(1)已知a=6,c=10,求b:
(1)已知a=5,b=12,求c:
(1)已知c=6,b=15,求a:
练习
如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
勾股树
练习
在RT△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
⑶ 若 c=17,a=8,则b=____
5
12
15
补充题
在Rt△ABC∠C=90°,BC:AC=3:4,AB=10,
则AC=_____?,BC=_____?
?
8
6
总结
1.勾股定理:
2.勾股的各种证明方法.
特殊三角形的相关计算
如图,在Rt△ABC中,∠C=90°, ∠B=45°,AC=1,则AB=(? ? ? ? ? )
A.2? ? ? ? ? B.1? ? ? ? ? ?C.? ? ? ? ? ? ? ?D.3
C
特殊三角形的相关计算
等边三角形的边长为12,则它的高为______
?
已知直角三角形两边求第三边
在直角三角形中,如果有两边为3,4,那么另一边为_________
勾股定理究竟是谁先发现的??
在西方人们认为勾股定理是毕达哥拉斯先发现的,并称之为“毕达哥拉斯定理”.?
不过早在公元前1120年左右中国的商高就在对话中说到:“故折矩,此为勾广三,股修四,经隅五.”?
你可能认为这是最早的勾股定理,但是具调查在公元前1900年的一块巴比伦上午泥板中,记载了15组勾股数. 所以古巴比伦人才是勾股定理最先的发现人.
勾股定理的来历
中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:
周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?”?
商高回答说:“数的产生来源于对方和圆这些形体饿认识.其中有一条原理:当直角三角形‘矩’得到的一条直角‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜‘弦’就必定是5.这个原理是大禹在治水的时候就总结出来的呵.”
商高定理
商高是公元前十一世纪的中国人.当时中国的朝代是西周,是奴隶社会时期.在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话.商高说:“…故折矩,勾广三,股修四,经隅五.”什么是“勾、股”呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫作"商高定理".
毕达哥拉斯简介
毕达哥拉斯出生于萨摩斯岛,自幼聪明好学,曾在名师门下学习几何,自然学和哲学.后来来到巴比伦,印度和埃及,吸收了阿拉伯文明和印度文明甚至中国文明的丰富营养.
大约在公元前530年,又返回萨摩斯岛,后来又迁居意大利的克罗通,创建了自己的学术.毕达哥拉斯学术认为数最崇高,最神秘,他们所讲的是整数.
可惜,朝气蓬勃的毕达哥拉斯到了晚年不仅学术保守,还反对新生事物,最后死与非命.
毕达哥拉斯定理
毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形磁砖,但毕达哥拉斯不只是欣赏磁砖的美丽,而是想到它们和[数]之间的关系,于是 拿了画笔并且蹲在地板上,选了一块磁砖以它的对角线 AB为边画一个正方形,他发现这个正方形面积恰好等于两块磁砖的面积和.他很好奇.... 于是再以两块磁砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块磁砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设: 任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.
百牛定理
希腊的著明数学家毕达格拉斯发现了这个定理,因此世界上许多国家都称勾股定理为“毕达格拉斯”定理.为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”.
总统与勾股定理
一个周末的傍晚,伽菲尔德突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形.于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀.”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心理很不是滋味.
总统与勾股定理
于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题.他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法.1881年,伽菲尔德就任美国第二十任总统后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法.
达芬奇与勾股定理
意大利文艺复兴时代的著名画家达芬奇也深深的沉醉在勾股定理的魅力中.
