人教版八年级数学下册课件:19.1.2函数的图像(2)(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.1.2函数的图像(2)(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 988.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:42:42 | ||
图片预览




文档简介
(共16张PPT)
1.会用描点法画出函数图象,能说出画函数图象的步骤;
2.会判断一个点是否在函数的图象上;
3.能初步通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合思想.
学习目标
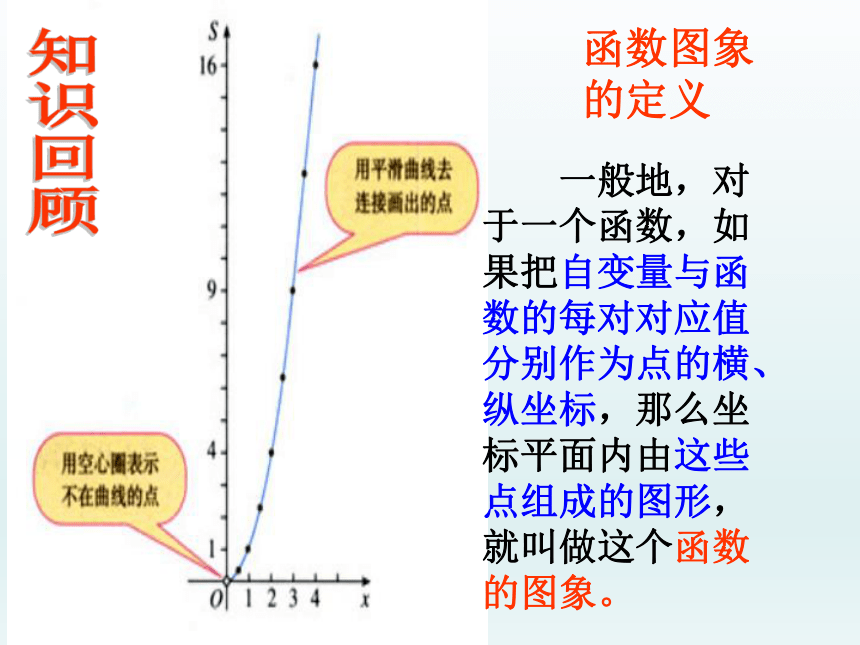
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就叫做这个函数的图象。
函数图象的定义
1、a是自变量x取值范围内的任意一个值,过点(a,0)画y轴的平行线,与图中曲线相交.下列哪个图中的曲线表示y是x的函数?为什么?
√
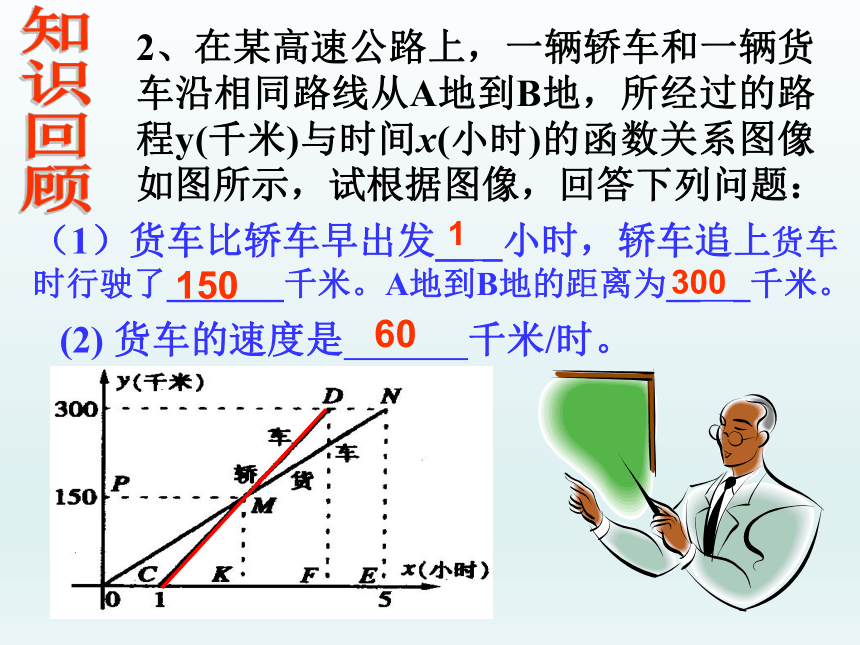
(1)货车比轿车早出发__ _小时,轿车追上货车时行驶了_______千米。A地到B地的距离为__ _千米。
2、在某高速公路上,一辆轿车和一辆货车沿相同路线从A地到B地,所经过的路程y(千米)与时间x(小时)的函数关系图像如图所示,试根据图像,回答下列问题:
1
150
300
60
(2) 货车的速度是 千米/时。
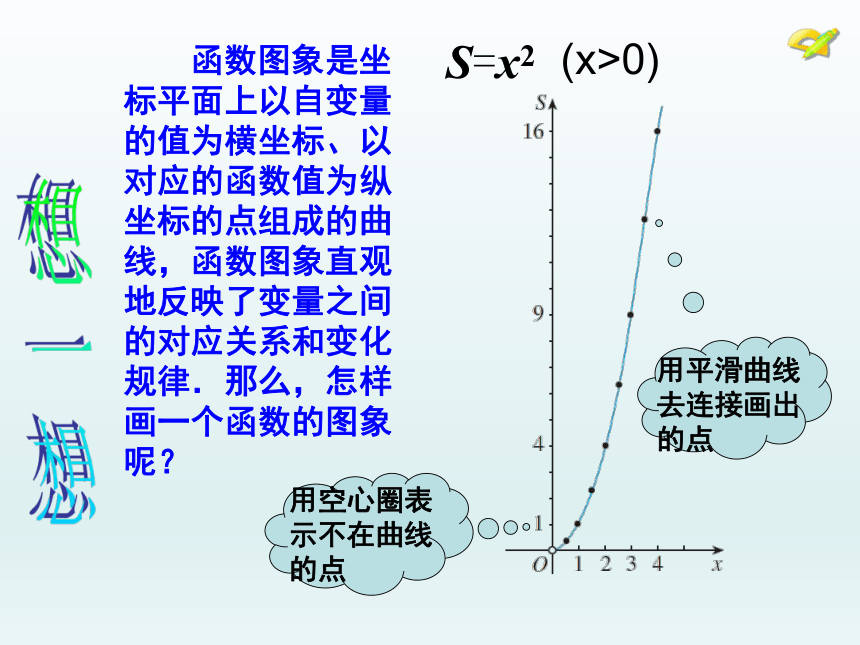
函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.那么,怎样画一个函数的图象呢?
用平滑曲线去连接画出的点
用空心圈表示不在曲线的点
S=x2
(x>0)
画函数图象一般分为哪几步?
1、列表:给出自变量与函数的 一些对应值
2、描点:以表中每对对应值为坐标,
在坐标平面内描出相应的点
3、连线:按照从左到右的顺序把所
描出的各点用平滑的曲线连接起来
例1 画出函数y=x+0.5的图象
①列表:
解:
试一试
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
这个函数的自变量取值范围是什么?为什么表格中前和3 后还有一栏要写省略号?
归纳:
作函数图象的一般步骤:
列表、描点、连线,
这种画函数图象的方法
称为描点法.
②描点:
1
3
2
x
y
1
3
2
-1
-3
-2
-1
-2
-3
o
③连线:
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
画出的图象是什么?图象上的点从左向右运动时,这个点是越来越高还是越来越低?能否用坐标解释这一图形特点?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
y=x+0.5
当自变量的值越来越大时,对应的函数值怎样变化?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
y=x+0.5
直线从左向右上升,即当x由小变大时,
y=x+0.5随之增大
(1)画出函数y=2x-1的图象;
做一做
练习1
(2)判断点A(-2.5,-4),B(1,3),
C(2.5,4)是否在函数y=2x-1的图象上。
(3).若点P(m,-3)是此函数图象上的一点,
求点P的坐标
x … 1 2 3 4 5 6 …
… …
例2 画出函数 (x﹥0) 的图象。
6
3
2
1.5
1.2
1
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,y的值随之减小。
练习2
(1)画出函数y=X2的图象。
(2)从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小?当x >0时呢?
1、函数图象的画法:
画函数图象的方法为列表、描点、
连线,通常称为描点法。
2、通过观察函数的图象,理解 函数的两个变量的关系,能够从所给的图象中获取信息从而解决简单问题。
作业:
教科书第83页习题19.1 第12 题;
画出下列函数的图象,并指出当x 的值增大时,
函数值怎样变化?
(1)y=4-2x ; (2)y=-2x2+1.
1.会用描点法画出函数图象,能说出画函数图象的步骤;
2.会判断一个点是否在函数的图象上;
3.能初步通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合思想.
学习目标
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就叫做这个函数的图象。
函数图象的定义
1、a是自变量x取值范围内的任意一个值,过点(a,0)画y轴的平行线,与图中曲线相交.下列哪个图中的曲线表示y是x的函数?为什么?
√
(1)货车比轿车早出发__ _小时,轿车追上货车时行驶了_______千米。A地到B地的距离为__ _千米。
2、在某高速公路上,一辆轿车和一辆货车沿相同路线从A地到B地,所经过的路程y(千米)与时间x(小时)的函数关系图像如图所示,试根据图像,回答下列问题:
1
150
300
60
(2) 货车的速度是 千米/时。
函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.那么,怎样画一个函数的图象呢?
用平滑曲线去连接画出的点
用空心圈表示不在曲线的点
S=x2
(x>0)
画函数图象一般分为哪几步?
1、列表:给出自变量与函数的 一些对应值
2、描点:以表中每对对应值为坐标,
在坐标平面内描出相应的点
3、连线:按照从左到右的顺序把所
描出的各点用平滑的曲线连接起来
例1 画出函数y=x+0.5的图象
①列表:
解:
试一试
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
这个函数的自变量取值范围是什么?为什么表格中前和3 后还有一栏要写省略号?
归纳:
作函数图象的一般步骤:
列表、描点、连线,
这种画函数图象的方法
称为描点法.
②描点:
1
3
2
x
y
1
3
2
-1
-3
-2
-1
-2
-3
o
③连线:
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
画出的图象是什么?图象上的点从左向右运动时,这个点是越来越高还是越来越低?能否用坐标解释这一图形特点?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
y=x+0.5
当自变量的值越来越大时,对应的函数值怎样变化?
2.5
1.5
0.5
y
x
-0.5
1
2
-1
O
y=x+0.5
直线从左向右上升,即当x由小变大时,
y=x+0.5随之增大
(1)画出函数y=2x-1的图象;
做一做
练习1
(2)判断点A(-2.5,-4),B(1,3),
C(2.5,4)是否在函数y=2x-1的图象上。
(3).若点P(m,-3)是此函数图象上的一点,
求点P的坐标
x … 1 2 3 4 5 6 …
… …
例2 画出函数 (x﹥0) 的图象。
6
3
2
1.5
1.2
1
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,y的值随之减小。
练习2
(1)画出函数y=X2的图象。
(2)从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小?当x >0时呢?
1、函数图象的画法:
画函数图象的方法为列表、描点、
连线,通常称为描点法。
2、通过观察函数的图象,理解 函数的两个变量的关系,能够从所给的图象中获取信息从而解决简单问题。
作业:
教科书第83页习题19.1 第12 题;
画出下列函数的图象,并指出当x 的值增大时,
函数值怎样变化?
(1)y=4-2x ; (2)y=-2x2+1.
