人教版八年级下册数学 18.2.2菱形课件(共40张PPT)
文档属性
| 名称 | 人教版八年级下册数学 18.2.2菱形课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:46:17 | ||
图片预览


文档简介
18.2.2 菱形
A
B
C
D
O
2、理解并掌握菱形的定义及性质,会用这些性质进行有关的证明和计算,会计算菱形的面积.
1、掌握菱形概念,知道菱形与平行四边形的关系.
3、理解并掌握菱形的定义及两个判定方法,会用这些判定方法进行有关的证明和计算.
有一组邻边相等的平行四边形叫做菱形.
AB=BC
四边形ABCD是菱形.
□ ABCD
菱形的定义
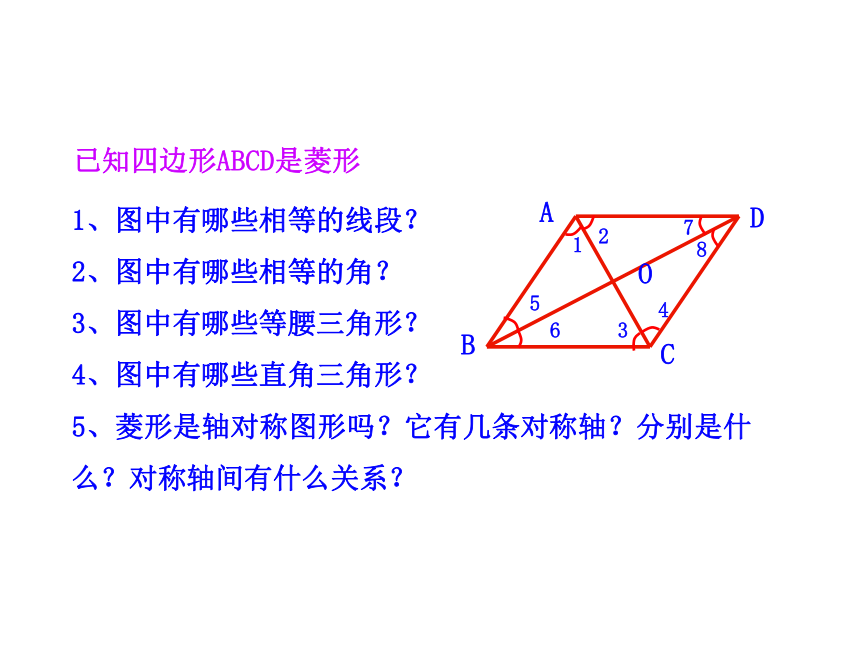
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
1、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些等腰三角形?
4、图中有哪些直角三角形?
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
已知四边形ABCD是菱形
A
B
C
D
O
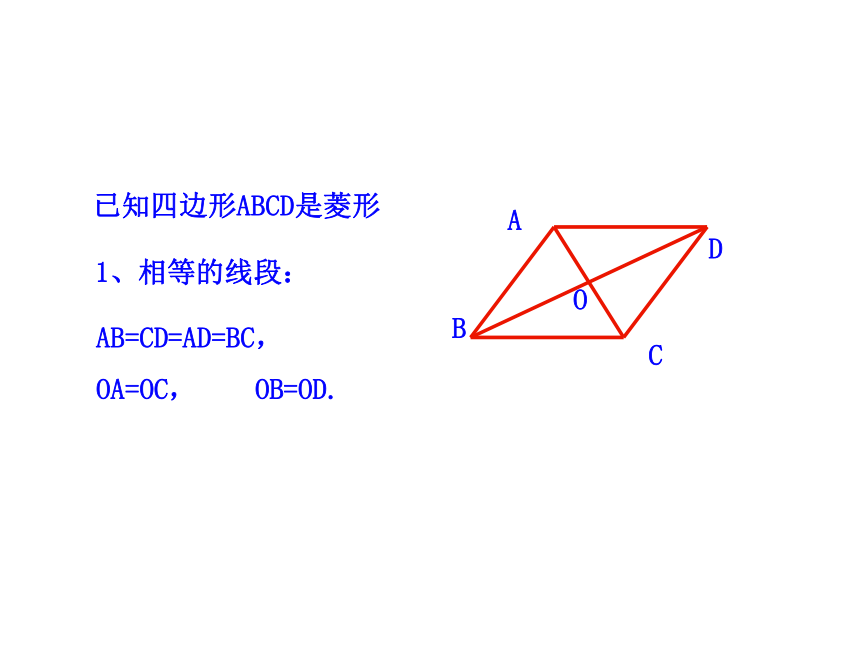
1、相等的线段:
AB=CD=AD=BC,
OA=OC, OB=OD.
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
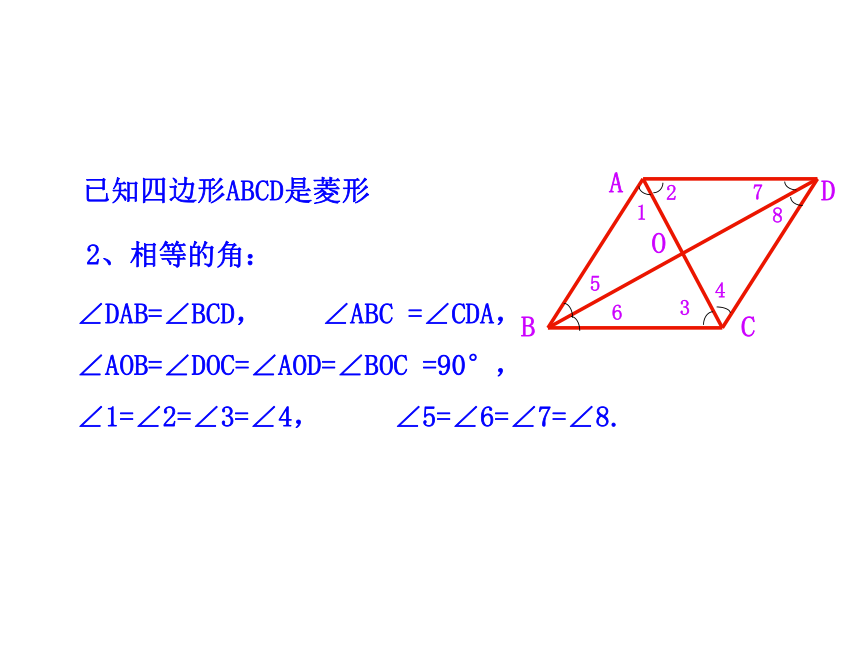
2、相等的角:
∠DAB=∠BCD, ∠ABC =∠CDA,
∠AOB=∠DOC=∠AOD=∠BOC =90°,
∠1=∠2=∠3=∠4, ∠5=∠6=∠7=∠8.
已知四边形ABCD是菱形
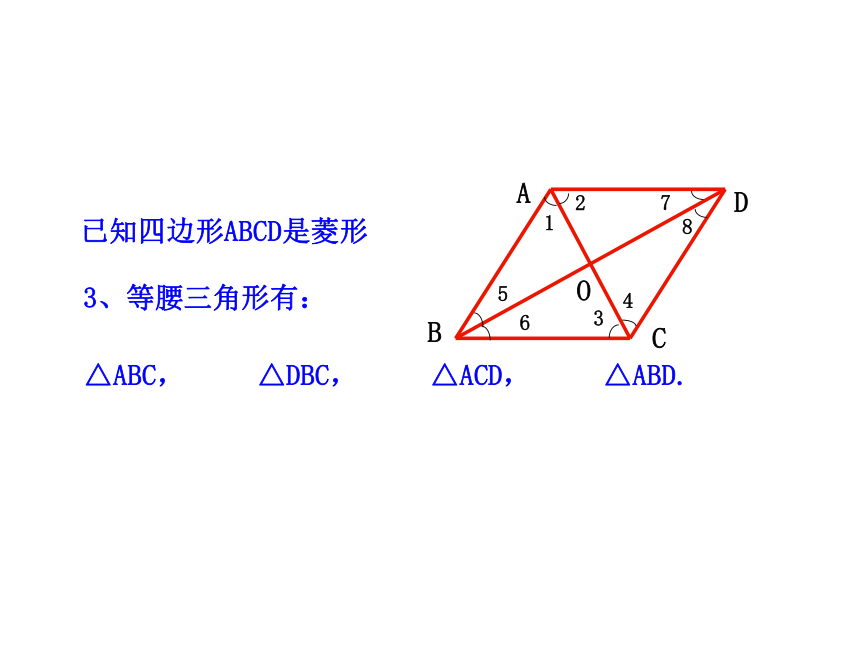
3、等腰三角形有:
△ABC, △DBC, △ACD, △ABD.
A
B
C
D
O
1
2
3
4
5
6
7
8
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
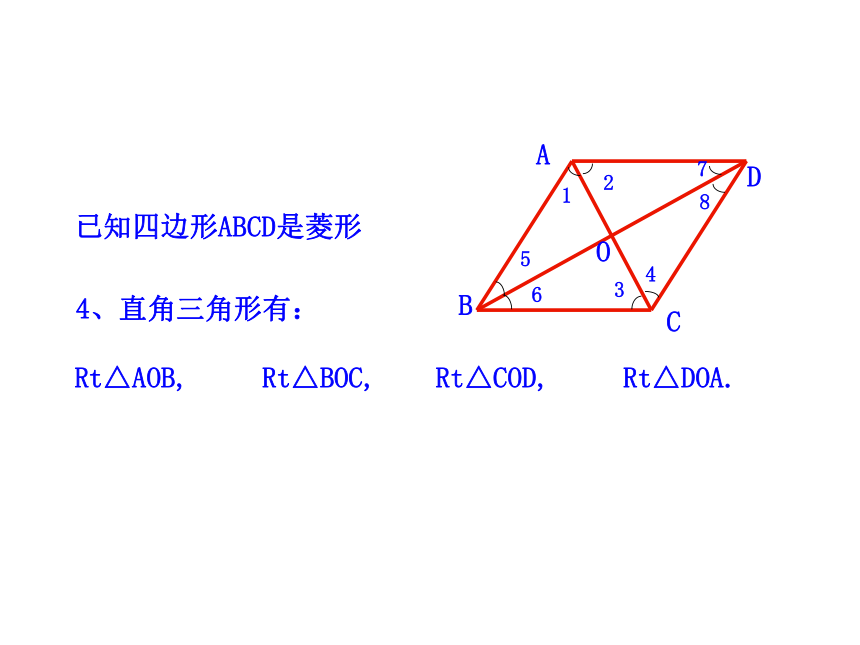
4、直角三角形有:
Rt△AOB, Rt△BOC, Rt△COD, Rt△DOA.
B
C
D
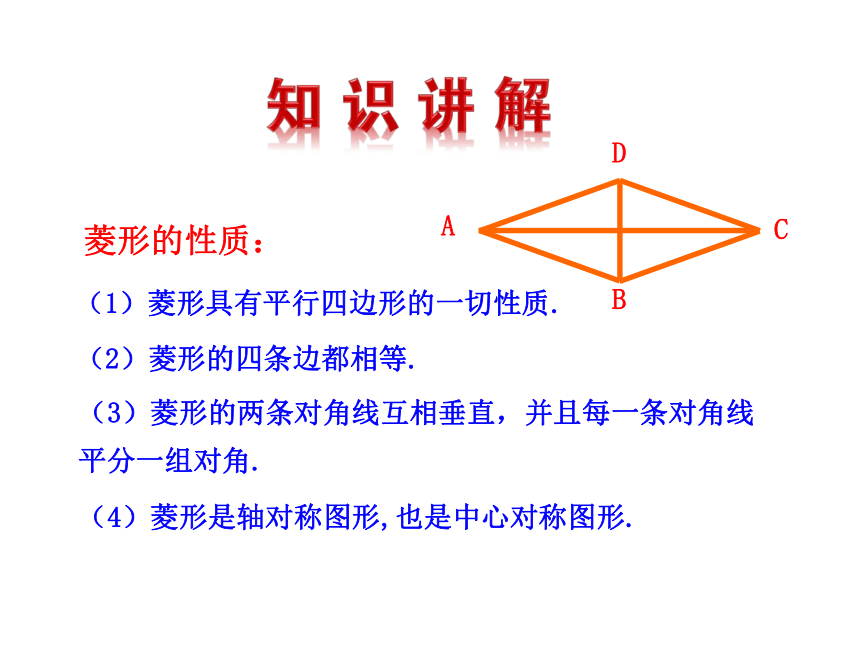
菱形的性质:
(1)菱形具有平行四边形的一切性质.
(2)菱形的四条边都相等.
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
(4)菱形是轴对称图形,也是中心对称图形.
A
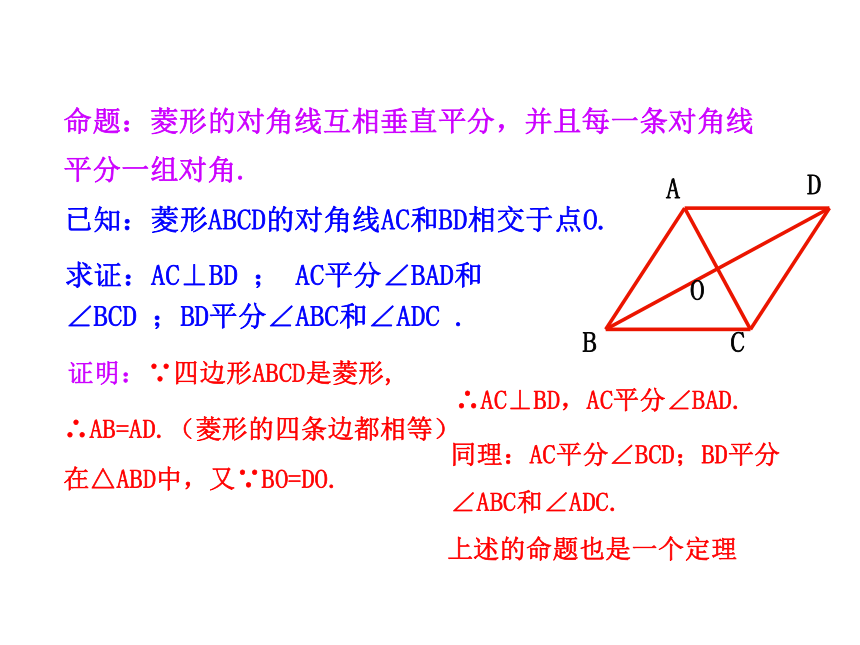
已知:菱形ABCD的对角线AC和BD相交于点O.
证明:∵四边形ABCD是菱形,
A
B
C
D
O
在△ABD中,又∵BO=DO.
∴AB=AD.(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD.
求证:AC⊥BD ; AC平分∠BAD和
∠BCD ;BD平分∠ABC和∠ADC .
命题:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
同理:AC平分∠BCD;BD平分
∠ABC和∠ADC.
上述的命题也是一个定理
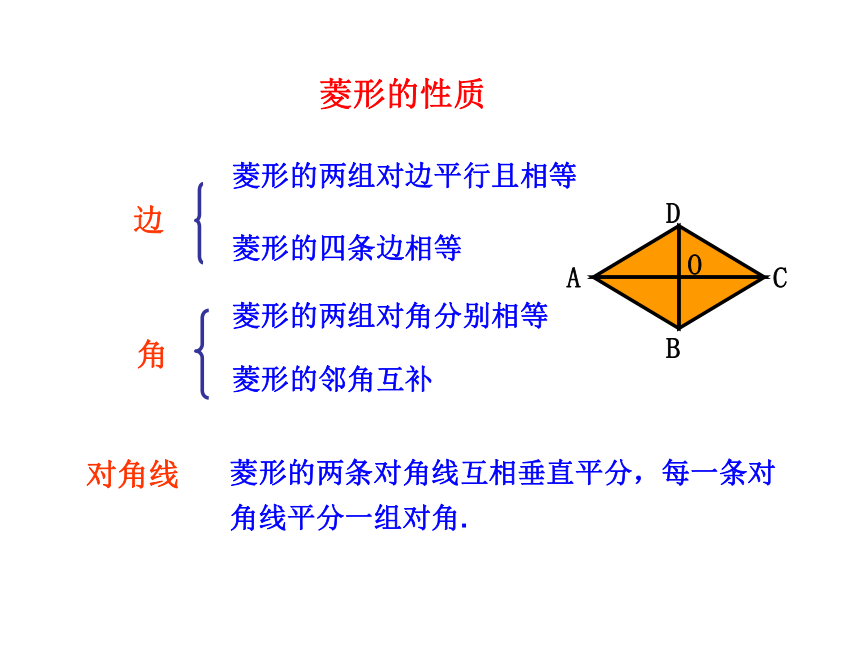
菱形的两组对边平行且相等
边
对角线
角
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
A
D
C
B
O
菱形的性质
【菱形的面积公式】
菱
形
A
B
C
D
O
E
S菱形=BC·AE
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗?
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
A
B
C
D
O
【例题】
两
一
【跟踪训练】
·
·
·
·
,而
所以菱形的
边长为4.
4
根据菱形的定义,可得菱形的第一个判定方法:
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
符号表示:
一组邻边相等的平行四边形叫做菱形
菱形的判定
求证: 是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD,
证明:
∴□ABCD是菱形.
又∵ AC ⊥ BD,
∵四边形ABCD是平行四边形,
∴OA=OC.
∴BA=BC,
A
B
C
D
O
定理:对角线互相垂直的平行四边形是菱形.
□ ABCD
□ ABCD
1、一组邻边相等的平行四边形是菱形.
2、对角线互相垂直的平行四边形是菱形.
3、四条边相等的四边形是菱形.
菱形常用的判定方法
【跟踪训练】
·
·
·
·
2.□ ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
A
B
C
D
O
矩
菱
矩
菱
,
,
即四边形AFCE是菱形.
4.
在
5.把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
菱形
1.(陕西·中考)若一个菱形的边长为2,则这个菱形两条对角线的平方和为( )
A.16 B.8 C.4 D.1
【解析】选A.设这个菱形两条对角线长分别为a,b.由菱形对角线互相垂直且平分,则
即a2+b2=16.
2.(连云港·中考)如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的
是( )
A.BA=BC B.AC、BD互相平分
C.AC=BD D.AB∥CD
【解析】选B.对角线互相垂直且平分的四边形是菱形.
3. (茂名·中考)如图,两条笔直的公路 , 相
交于点O,村庄C的村民在公路的旁边建三个加工厂A,
B,D,已知AB=BC=CD=DA=5公里,村庄C到公路 的距离
为4公里,则村庄C到公路 的距离是
A.3公里 B.4公里
C.5公里 D.6公里
【解析】选B,连接AC,由题意知四边形ABCD是菱形,所
以AC为∠DAB的平分线,所以点C到 , 的距离相等,
故选B.
4.(珠海·中考)如图,P是菱形ABCD对角线BD上
一点,PE⊥AB于点E,PE=4 cm,则点P到BC的距离
是____cm.
【解析】菱形对角线平分一组对角,且角平分线上的点到角两边的距离相等,故点P到BC的距离是4 cm.
答案:4
5.(温州·中考)如图,在
□ ABCD中,EF∥BD,分别交BC,CD于
点P,Q,交AB,AD的延长线于点E,F.
已知BE=BP.
求证:(1)∠E=∠F.
(2)□ ABCD是菱形.
【证明】(1)在□ABCD中,BC∥AD,
∴∠1=∠F.∵BE=BP,∴∠E=∠1,∴∠E=∠F.
(2)∵BD∥EF,
∴∠2=∠E,∠3=∠F.
∵∠E=∠F,
∴∠2=∠3,
∴AB=AD,
∴□ ABCD是菱形.
6.(郴州·中考)一种千斤顶利用了四边形的不稳定性.
如图,其基本形状是一个菱形,中间通过螺杆连接,转动
手柄可改变∠ADC的大小(菱形的边长不变),从而改变
千斤顶的高度(即A,C之间的距离).若AB=40 cm,当∠ADC
从60°变为120°时,千斤顶升高了多少?( ≈1.414,
≈1.732,结果保留整数)
【解析】连接AC,与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,∠ADB=∠CDB,AC=2AO.
当∠ADC=60°时,△ADC是等边三角形.
∴AC=AD=AB=40cm.
当∠ADC=120°时,
∴∠ADO=60°,∠OAD=30°,
又AD=40,∴OD=20.
本节课主要学习了菱形的定义、性质、判定:
1、掌握菱形的定义、性质、判定.
2、弄清菱形的性质、判定的区别与联系.
3、会应用菱形的知识解决有关计算和证明问题
一、菱形的定义
有一组_____相等的平行四边形叫做菱形.
二、菱形的性质
1.菱形的四条边都_____.
2.菱形的两条对角线互相_____,并且每一条对角线_____
一组对角.
菱形的面积等于它的两条对角线之积的一半.
邻边
相等
垂直
平分
A
B
C
D
O
2、理解并掌握菱形的定义及性质,会用这些性质进行有关的证明和计算,会计算菱形的面积.
1、掌握菱形概念,知道菱形与平行四边形的关系.
3、理解并掌握菱形的定义及两个判定方法,会用这些判定方法进行有关的证明和计算.
有一组邻边相等的平行四边形叫做菱形.
AB=BC
四边形ABCD是菱形.
□ ABCD
菱形的定义
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
1、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些等腰三角形?
4、图中有哪些直角三角形?
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
已知四边形ABCD是菱形
A
B
C
D
O
1、相等的线段:
AB=CD=AD=BC,
OA=OC, OB=OD.
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
2、相等的角:
∠DAB=∠BCD, ∠ABC =∠CDA,
∠AOB=∠DOC=∠AOD=∠BOC =90°,
∠1=∠2=∠3=∠4, ∠5=∠6=∠7=∠8.
已知四边形ABCD是菱形
3、等腰三角形有:
△ABC, △DBC, △ACD, △ABD.
A
B
C
D
O
1
2
3
4
5
6
7
8
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
4、直角三角形有:
Rt△AOB, Rt△BOC, Rt△COD, Rt△DOA.
B
C
D
菱形的性质:
(1)菱形具有平行四边形的一切性质.
(2)菱形的四条边都相等.
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
(4)菱形是轴对称图形,也是中心对称图形.
A
已知:菱形ABCD的对角线AC和BD相交于点O.
证明:∵四边形ABCD是菱形,
A
B
C
D
O
在△ABD中,又∵BO=DO.
∴AB=AD.(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD.
求证:AC⊥BD ; AC平分∠BAD和
∠BCD ;BD平分∠ABC和∠ADC .
命题:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
同理:AC平分∠BCD;BD平分
∠ABC和∠ADC.
上述的命题也是一个定理
菱形的两组对边平行且相等
边
对角线
角
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
A
D
C
B
O
菱形的性质
【菱形的面积公式】
菱
形
A
B
C
D
O
E
S菱形=BC·AE
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗?
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
A
B
C
D
O
【例题】
两
一
【跟踪训练】
·
·
·
·
,而
所以菱形的
边长为4.
4
根据菱形的定义,可得菱形的第一个判定方法:
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
符号表示:
一组邻边相等的平行四边形叫做菱形
菱形的判定
求证: 是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD,
证明:
∴□ABCD是菱形.
又∵ AC ⊥ BD,
∵四边形ABCD是平行四边形,
∴OA=OC.
∴BA=BC,
A
B
C
D
O
定理:对角线互相垂直的平行四边形是菱形.
□ ABCD
□ ABCD
1、一组邻边相等的平行四边形是菱形.
2、对角线互相垂直的平行四边形是菱形.
3、四条边相等的四边形是菱形.
菱形常用的判定方法
【跟踪训练】
·
·
·
·
2.□ ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
A
B
C
D
O
矩
菱
矩
菱
,
,
即四边形AFCE是菱形.
4.
在
5.把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
菱形
1.(陕西·中考)若一个菱形的边长为2,则这个菱形两条对角线的平方和为( )
A.16 B.8 C.4 D.1
【解析】选A.设这个菱形两条对角线长分别为a,b.由菱形对角线互相垂直且平分,则
即a2+b2=16.
2.(连云港·中考)如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的
是( )
A.BA=BC B.AC、BD互相平分
C.AC=BD D.AB∥CD
【解析】选B.对角线互相垂直且平分的四边形是菱形.
3. (茂名·中考)如图,两条笔直的公路 , 相
交于点O,村庄C的村民在公路的旁边建三个加工厂A,
B,D,已知AB=BC=CD=DA=5公里,村庄C到公路 的距离
为4公里,则村庄C到公路 的距离是
A.3公里 B.4公里
C.5公里 D.6公里
【解析】选B,连接AC,由题意知四边形ABCD是菱形,所
以AC为∠DAB的平分线,所以点C到 , 的距离相等,
故选B.
4.(珠海·中考)如图,P是菱形ABCD对角线BD上
一点,PE⊥AB于点E,PE=4 cm,则点P到BC的距离
是____cm.
【解析】菱形对角线平分一组对角,且角平分线上的点到角两边的距离相等,故点P到BC的距离是4 cm.
答案:4
5.(温州·中考)如图,在
□ ABCD中,EF∥BD,分别交BC,CD于
点P,Q,交AB,AD的延长线于点E,F.
已知BE=BP.
求证:(1)∠E=∠F.
(2)□ ABCD是菱形.
【证明】(1)在□ABCD中,BC∥AD,
∴∠1=∠F.∵BE=BP,∴∠E=∠1,∴∠E=∠F.
(2)∵BD∥EF,
∴∠2=∠E,∠3=∠F.
∵∠E=∠F,
∴∠2=∠3,
∴AB=AD,
∴□ ABCD是菱形.
6.(郴州·中考)一种千斤顶利用了四边形的不稳定性.
如图,其基本形状是一个菱形,中间通过螺杆连接,转动
手柄可改变∠ADC的大小(菱形的边长不变),从而改变
千斤顶的高度(即A,C之间的距离).若AB=40 cm,当∠ADC
从60°变为120°时,千斤顶升高了多少?( ≈1.414,
≈1.732,结果保留整数)
【解析】连接AC,与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,∠ADB=∠CDB,AC=2AO.
当∠ADC=60°时,△ADC是等边三角形.
∴AC=AD=AB=40cm.
当∠ADC=120°时,
∴∠ADO=60°,∠OAD=30°,
又AD=40,∴OD=20.
本节课主要学习了菱形的定义、性质、判定:
1、掌握菱形的定义、性质、判定.
2、弄清菱形的性质、判定的区别与联系.
3、会应用菱形的知识解决有关计算和证明问题
一、菱形的定义
有一组_____相等的平行四边形叫做菱形.
二、菱形的性质
1.菱形的四条边都_____.
2.菱形的两条对角线互相_____,并且每一条对角线_____
一组对角.
菱形的面积等于它的两条对角线之积的一半.
邻边
相等
垂直
平分
