人教版八年级下册数学 18.2.3正方形课件(共34张PPT)
文档属性
| 名称 | 人教版八年级下册数学 18.2.3正方形课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览


文档简介
18.2.3正方形
回顾:平行四边形,矩形与菱形有哪些性质?
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等且互相平分
边:
对边平行且相等
具有平行四边形所有性质
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
对角相等,邻角互补
具有平行四边形一切性质
角:
学习目标:
1.理解正方形与平行四边形、矩形、菱形概念之间的联系和区别;
2.能用正方形的定义、性质和判定进行推理与计算.
学习重点:
正方形与平行四边形、矩形、菱形的联系.
创设情境 引入新知
除了矩形和菱形外,还有什么特殊的平行四边形吗?
正方形
怎样研究这类图形?
先看看我们是怎样研究矩形和菱形的.
创设情境 引入新课
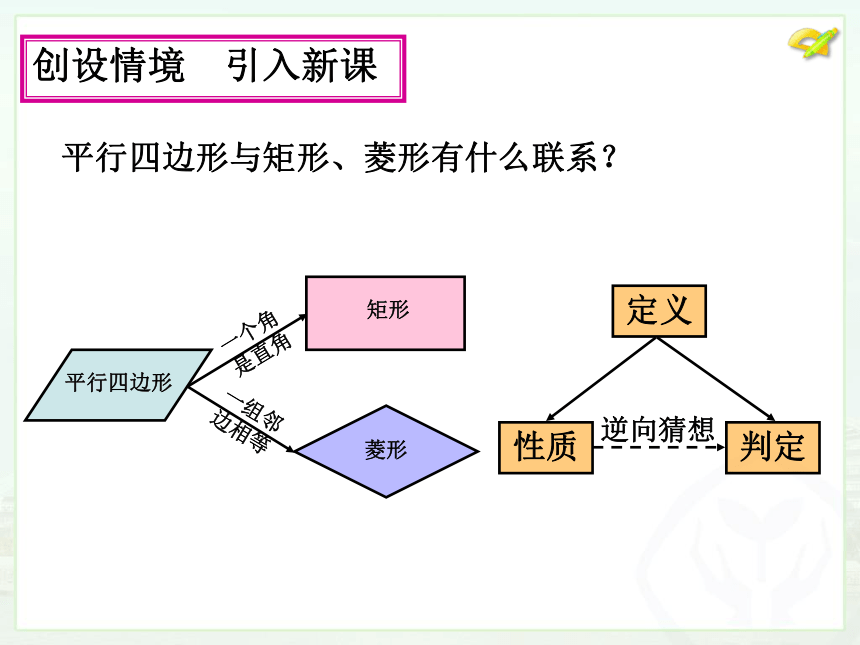
平行四边形与矩形、菱形有什么联系?
性质
定义
判定
逆向猜想
一个角
是直角
一组邻
边相等
平行四边形
矩形
菱形
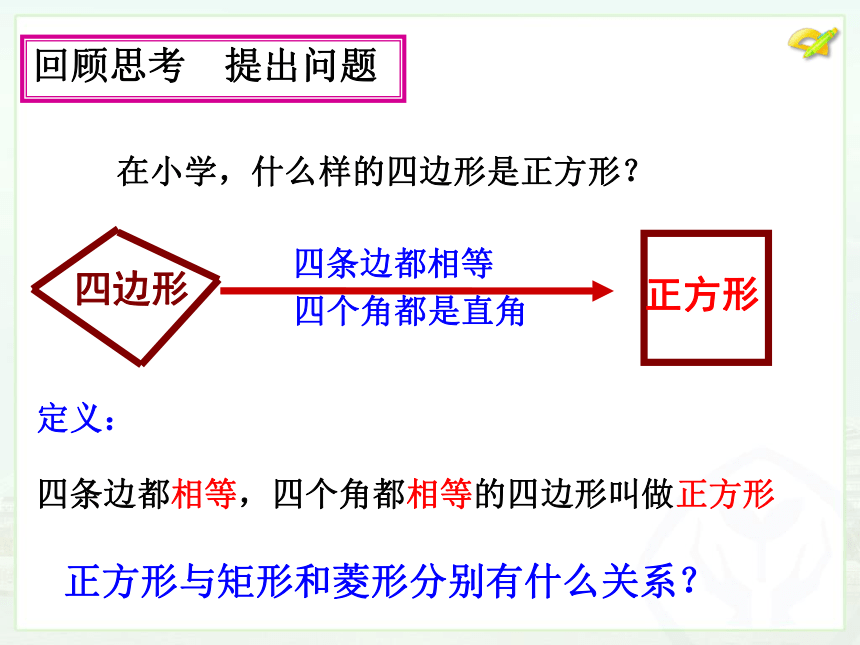
回顾思考 提出问题
在小学,什么样的四边形是正方形?
正方形与矩形和菱形分别有什么关系?
正方形
定义:
四条边都相等,四个角都相等的四边形叫做正方形
四边形
四条边都相等
四个角都是直角
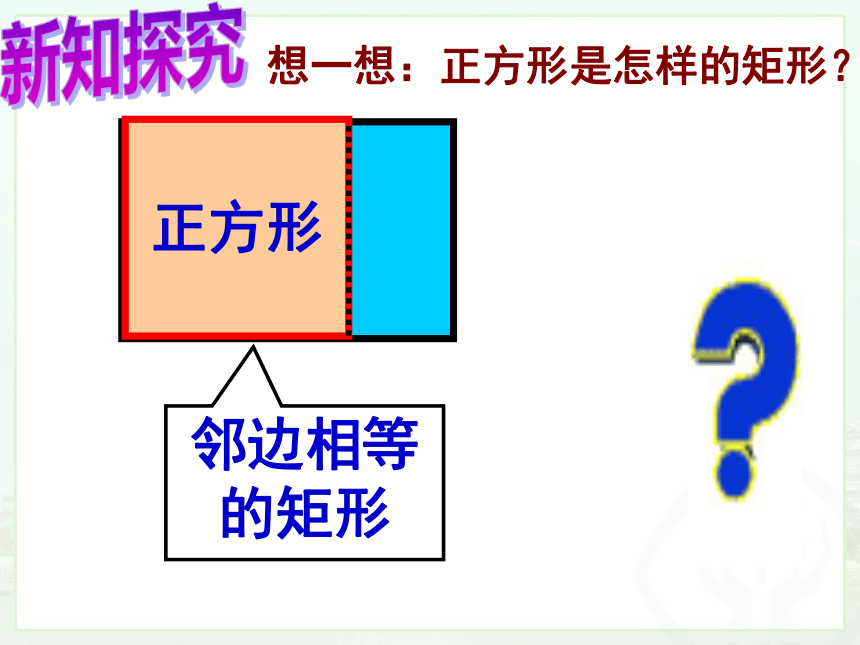
邻边相等的矩形
想一想:正方形是怎样的矩形?
矩形
正方形
新知探究
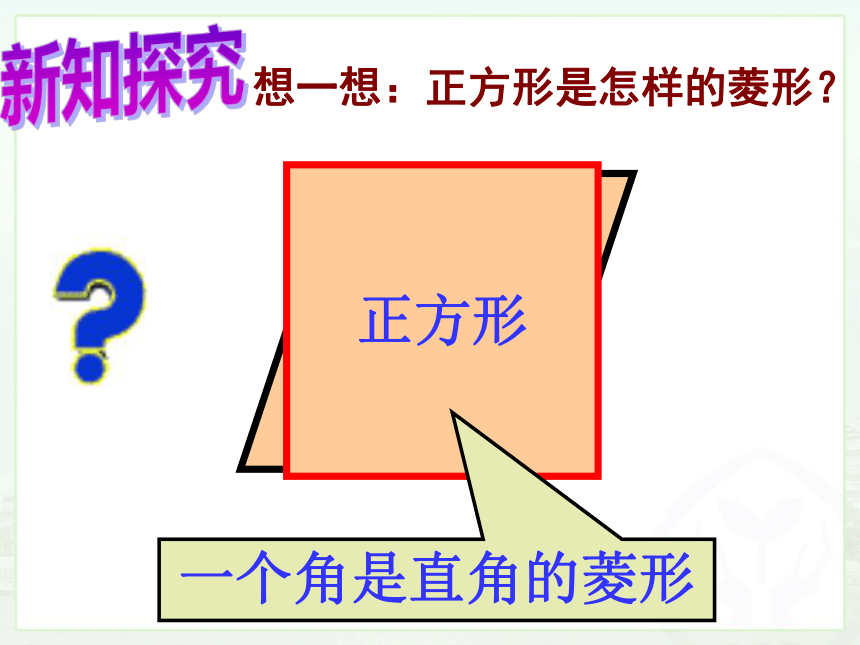
菱形
正方形
一个角是直角的菱形
想一想:正方形是怎样的菱形?
新知探究
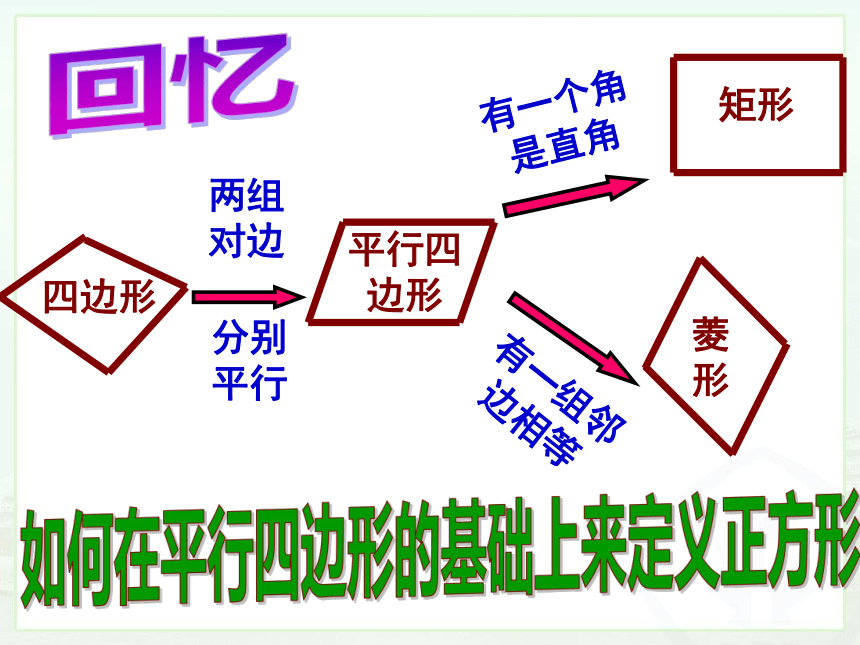
两组对边
分别平行
有一个角是直角
有一组邻边相等
四边形
平行四边形
矩形
菱形
回忆
如何在平行四边形的基础上来定义正方形
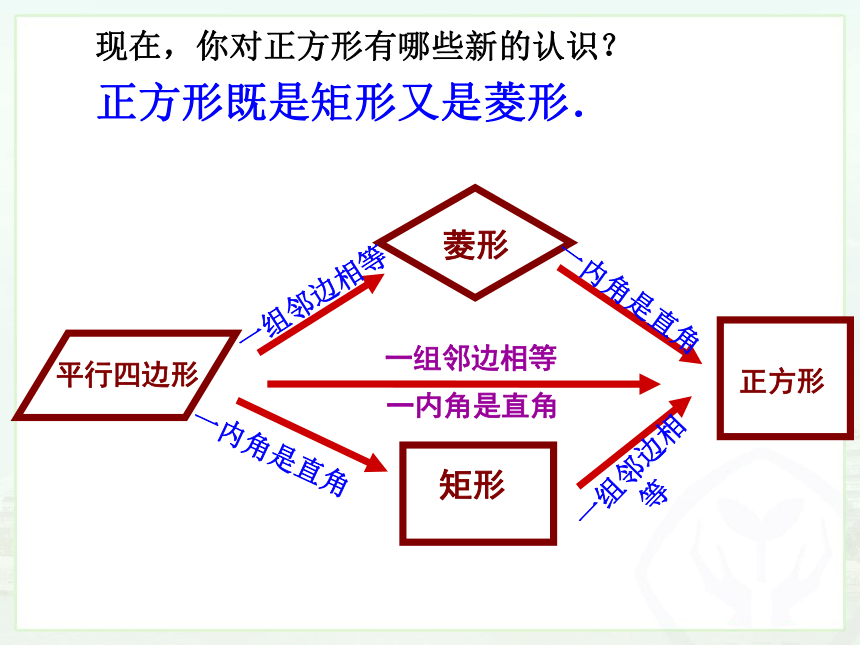
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
一组邻边相等
一内角是直角
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
边
对角线
角
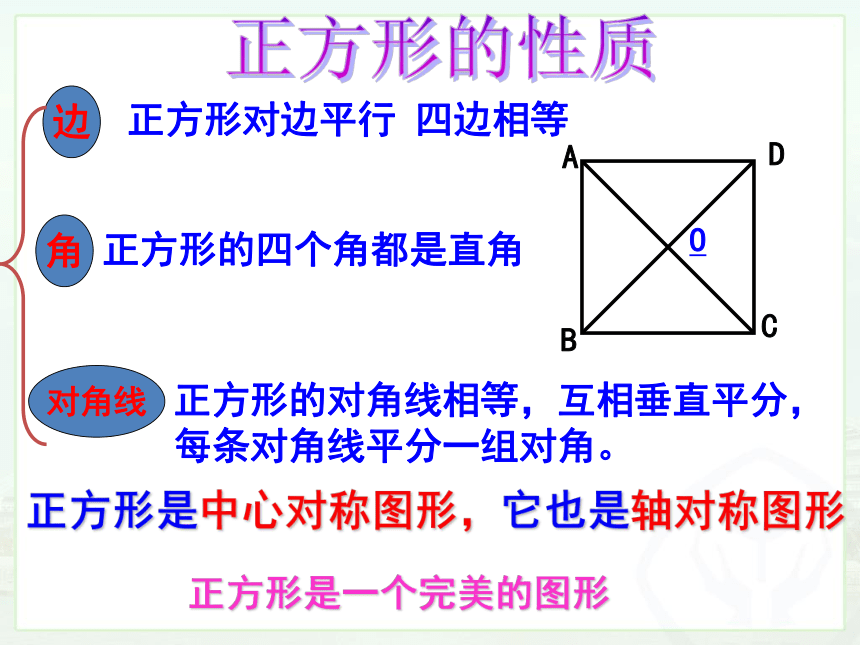
正方形的性质
正方形对边平行 四边相等
正方形的四个角都是直角
正方形的对角线相等,互相垂直平分,每条对角线平分一组对角。
A
B
C
D
O
正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形
为什么说正方形是一个完美的图形?
对称性
讨论3
特征
正方形是中心对称图形,对称中心为点O
它也是轴对称图形,有4条对称轴
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分
(2)具有矩形的一切性质
四个角都是直角,对角线相等
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角
O
A
B
C
D
(A)
(B)
(C)
(D)
总结:平行四边形、矩形、菱形、正方形的对称性
平行四边形
中心对称图形
(对角线的交点)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(四条)
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
平行四边形、矩形、菱形、正方形之间关系
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
菱形性质
矩形性质
正方形的性质=
回顾平行四边形,矩形,菱形的性质,完成表格前三列
平行四边形
矩 形 (所特有)
菱形 (所特有)
边
角
对角线
图形的对称性
对边平行且相等
四条边相等
对边平行且四条边相等
对角相等邻角互补
四个角都是直角
四个角都是直角
对角线互相平分
对角线相等
对角线互相垂直,每条对角线平分一组对角
对角线相等且互相垂直平分,每条对角线平分一组对角
中心对称图形
既是中心对称图形又是轴对称图形
既是中心对称图形又是轴对称图形
既是中心对称图形又是轴对称图形
图形
性质
分类
正方形
类
比
归
纳
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
选一选
2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
要判定一个三角形是等腰直
角三角形需要什么条件?判定两
个三角形全等的条件又是什么?
图中共有多少个等腰直角三
角形?
应用新知 解决问题
例1 求证:正方形的两条对角线把这个正方形分
成四个全等的等腰直角三角形.
O
A
B
C
D
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
A
D
A
B
C
E
课本 练习P59
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=30m,EB=10m
∴ S正方形ABCD=( )2=800(m2)
∴
∴
细心引导 探究新知
怎样判定一个矩形是正方形?怎样判定一个菱形是
正方形?
怎样判定一个平行四边形是正方形?
既是矩形又是菱形的四边形是正方形.
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
定义法
菱形法
矩形法
①四条边相等,四个角都是直角
②对角线互相垂直、平分且相等
四边形
正方形
以四边形为基础:
既是菱形又是矩形的四边形是正方形。
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
√
√
√
×
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )
√
快速反应
判断题:
(6)正方形一定是矩形.( )
(7)正方形一定是菱形.( )
(8)菱形一定是正方形.( )
(9)矩形一定是正方形.( )
(10)正方形、矩形、菱形都是平行四边形. ( )
√
√
√
×
×
(12)正方形是轴对称图形,一共有2条对称轴( )
(13)四个角都相等的四边形是正方形 ( )
(14)四条边都相等的四边形是正方形 ( )
×
×
×
4.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______.
练一练
2
2
4
6
36
5.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______,
应用新知 解决问题
例2 如图,顺次连接正方形ABCD各边的中点,得
到四边形EFGH.求证:四边形EFGH也是正方形.
E
A
B
C
D
F
H
G
应用新知 解决问题
E
A
B
C
D
F
H
G
变式 如图,E,F,G,H分别是各边上的点,且
AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
学习了本节课你有哪些收获?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展
如何设计花坛?
八年级 数学
第十九章 四边形
数一数图中正方形的个数,你发现了什么?
多
多
多
( )个( )个 ( )个 ( )个
第n个图中正方形有 个
3n-1
长见识
八年级 数学
第十九章 四边形
回顾:平行四边形,矩形与菱形有哪些性质?
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等且互相平分
边:
对边平行且相等
具有平行四边形所有性质
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
对角相等,邻角互补
具有平行四边形一切性质
角:
学习目标:
1.理解正方形与平行四边形、矩形、菱形概念之间的联系和区别;
2.能用正方形的定义、性质和判定进行推理与计算.
学习重点:
正方形与平行四边形、矩形、菱形的联系.
创设情境 引入新知
除了矩形和菱形外,还有什么特殊的平行四边形吗?
正方形
怎样研究这类图形?
先看看我们是怎样研究矩形和菱形的.
创设情境 引入新课
平行四边形与矩形、菱形有什么联系?
性质
定义
判定
逆向猜想
一个角
是直角
一组邻
边相等
平行四边形
矩形
菱形
回顾思考 提出问题
在小学,什么样的四边形是正方形?
正方形与矩形和菱形分别有什么关系?
正方形
定义:
四条边都相等,四个角都相等的四边形叫做正方形
四边形
四条边都相等
四个角都是直角
邻边相等的矩形
想一想:正方形是怎样的矩形?
矩形
正方形
新知探究
菱形
正方形
一个角是直角的菱形
想一想:正方形是怎样的菱形?
新知探究
两组对边
分别平行
有一个角是直角
有一组邻边相等
四边形
平行四边形
矩形
菱形
回忆
如何在平行四边形的基础上来定义正方形
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
一组邻边相等
一内角是直角
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
边
对角线
角
正方形的性质
正方形对边平行 四边相等
正方形的四个角都是直角
正方形的对角线相等,互相垂直平分,每条对角线平分一组对角。
A
B
C
D
O
正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形
为什么说正方形是一个完美的图形?
对称性
讨论3
特征
正方形是中心对称图形,对称中心为点O
它也是轴对称图形,有4条对称轴
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分
(2)具有矩形的一切性质
四个角都是直角,对角线相等
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角
O
A
B
C
D
(A)
(B)
(C)
(D)
总结:平行四边形、矩形、菱形、正方形的对称性
平行四边形
中心对称图形
(对角线的交点)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(两条)
即是中心对称图形,
又是轴对称图形(四条)
正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
(1)
(2)
(3)
(4)
四边形
平行四边形
矩形
菱形
正方形
平行四边形
矩形
四边形
菱形
正
方
形
平行四边形、矩形、菱形、正方形之间关系
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
菱形性质
矩形性质
正方形的性质=
回顾平行四边形,矩形,菱形的性质,完成表格前三列
平行四边形
矩 形 (所特有)
菱形 (所特有)
边
角
对角线
图形的对称性
对边平行且相等
四条边相等
对边平行且四条边相等
对角相等邻角互补
四个角都是直角
四个角都是直角
对角线互相平分
对角线相等
对角线互相垂直,每条对角线平分一组对角
对角线相等且互相垂直平分,每条对角线平分一组对角
中心对称图形
既是中心对称图形又是轴对称图形
既是中心对称图形又是轴对称图形
既是中心对称图形又是轴对称图形
图形
性质
分类
正方形
类
比
归
纳
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
选一选
2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
要判定一个三角形是等腰直
角三角形需要什么条件?判定两
个三角形全等的条件又是什么?
图中共有多少个等腰直角三
角形?
应用新知 解决问题
例1 求证:正方形的两条对角线把这个正方形分
成四个全等的等腰直角三角形.
O
A
B
C
D
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
A
D
A
B
C
E
课本 练习P59
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=30m,EB=10m
∴ S正方形ABCD=( )2=800(m2)
∴
∴
细心引导 探究新知
怎样判定一个矩形是正方形?怎样判定一个菱形是
正方形?
怎样判定一个平行四边形是正方形?
既是矩形又是菱形的四边形是正方形.
平行四边形
正方形
一组邻边相等
一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
定义法
菱形法
矩形法
①四条边相等,四个角都是直角
②对角线互相垂直、平分且相等
四边形
正方形
以四边形为基础:
既是菱形又是矩形的四边形是正方形。
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
√
√
√
×
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )
√
快速反应
判断题:
(6)正方形一定是矩形.( )
(7)正方形一定是菱形.( )
(8)菱形一定是正方形.( )
(9)矩形一定是正方形.( )
(10)正方形、矩形、菱形都是平行四边形. ( )
√
√
√
×
×
(12)正方形是轴对称图形,一共有2条对称轴( )
(13)四个角都相等的四边形是正方形 ( )
(14)四条边都相等的四边形是正方形 ( )
×
×
×
4.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______.
练一练
2
2
4
6
36
5.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______,
应用新知 解决问题
例2 如图,顺次连接正方形ABCD各边的中点,得
到四边形EFGH.求证:四边形EFGH也是正方形.
E
A
B
C
D
F
H
G
应用新知 解决问题
E
A
B
C
D
F
H
G
变式 如图,E,F,G,H分别是各边上的点,且
AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
学习了本节课你有哪些收获?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展
如何设计花坛?
八年级 数学
第十九章 四边形
数一数图中正方形的个数,你发现了什么?
多
多
多
( )个( )个 ( )个 ( )个
第n个图中正方形有 个
3n-1
长见识
八年级 数学
第十九章 四边形
