人教版八年级下册数学课件:18.2.3正方形 习题课(共21张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:18.2.3正方形 习题课(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 613.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:50:45 | ||
图片预览



文档简介
A
B
C
D
O
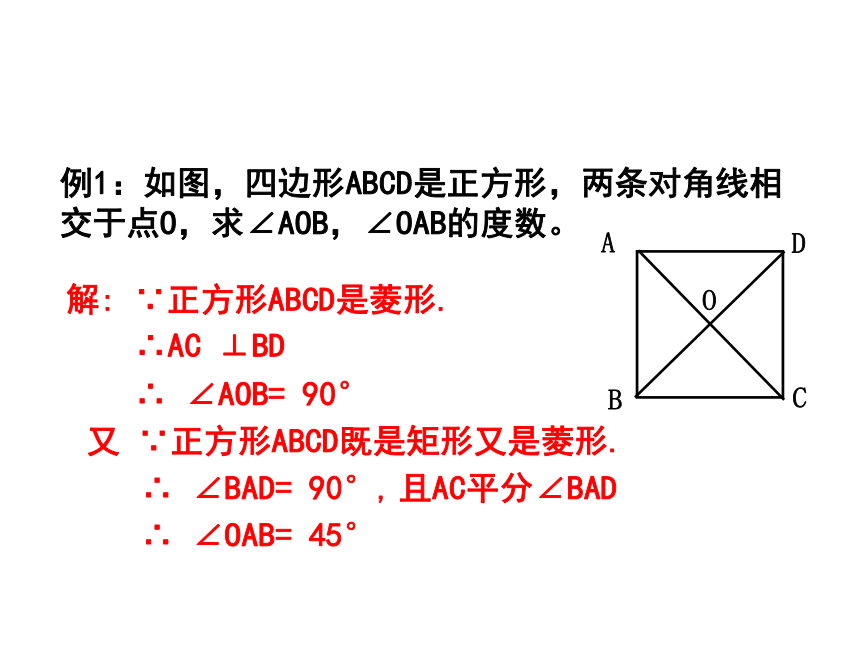
解: ∵正方形ABCD是菱形.
∴AC ⊥BD
∴ ∠AOB= 90°
又 ∵正方形ABCD既是矩形又是菱形.
∴ ∠BAD= 90°, 且AC平分∠BAD
∴ ∠OAB= 45°
例1:如图,四边形ABCD是正方形,两条对角线相交于点O,求∠AOB,∠OAB的度数。
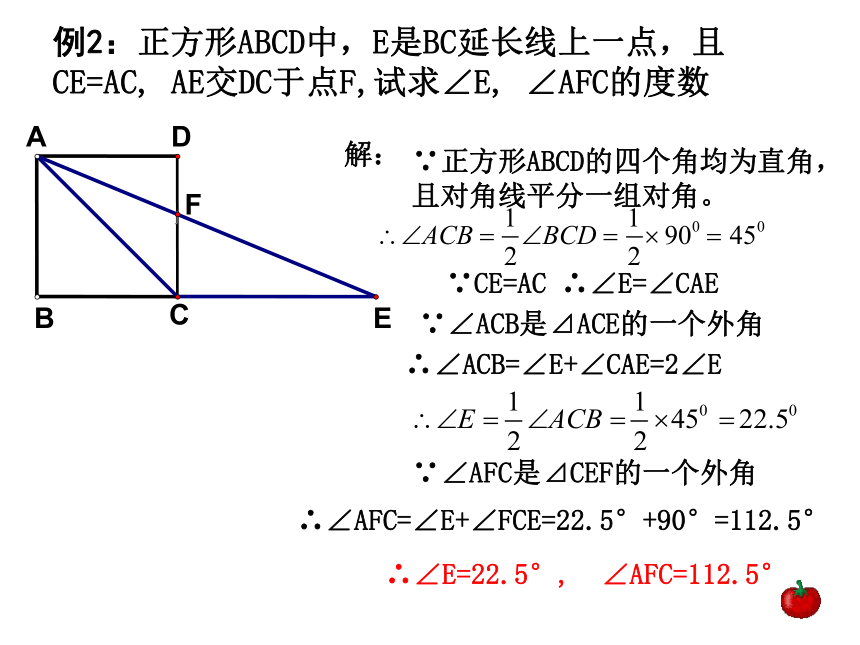
例2:正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
解:
∵正方形ABCD的四个角均为直角,且对角线平分一组对角。
∵CE=AC
∴∠E=∠CAE
∵∠ACB是⊿ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是⊿CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
j
F
E
A
B
D
C
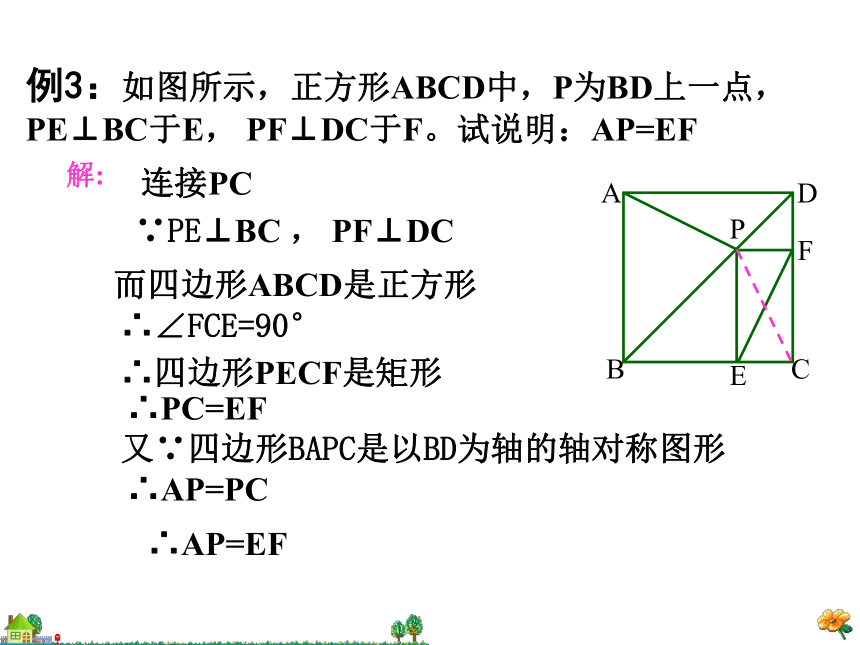
例3:如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF
A
B
C
D
P
E
F
解:
连接PC
∵PE⊥BC , PF⊥DC
而四边形ABCD是正方形
∴∠FCE=90°
∴四边形PECF是矩形
∴PC=EF
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=EF
小试牛刀
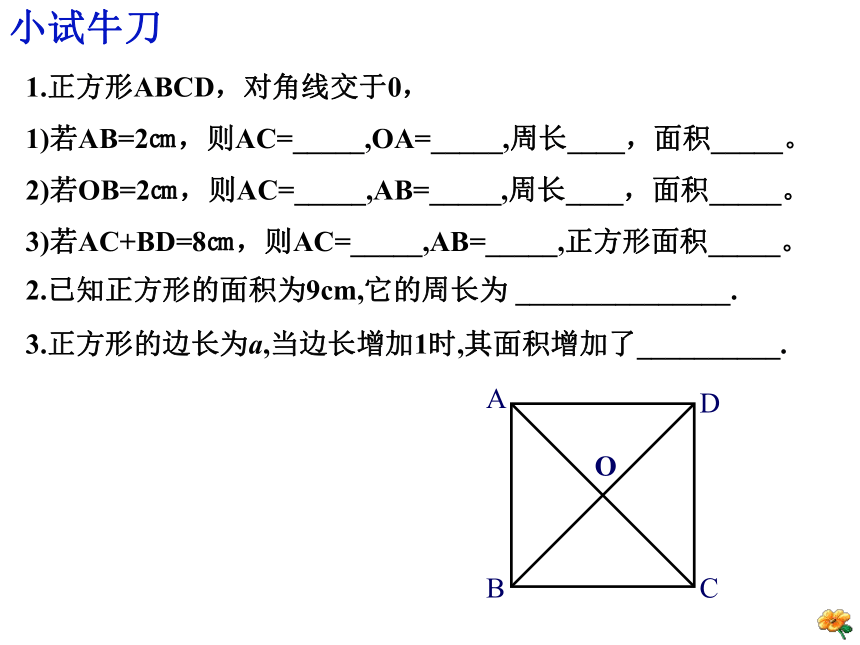
1.正方形ABCD,对角线交于0,
1)若AB=2㎝,则AC=_____,OA=_____,周长____,面积_____。
2)若OB=2㎝,则AC=_____,AB=_____,周长____,面积_____。
3)若AC+BD=8㎝,则AC=_____,AB=_____,正方形面积_____。
2.已知正方形的面积为9cm,它的周长为 _______________.
3.正方形的边长为a,当边长增加1时,其面积增加了__________.
O
A
B
C
D
4.正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
5.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
随堂练习
用10米长的篱笆围成一个四边形菜地,如何确定面积最大的四边形的形状,面积为多少?
在长度给定的情况下,围成的四边形中,
正方形的面积最大。
6.
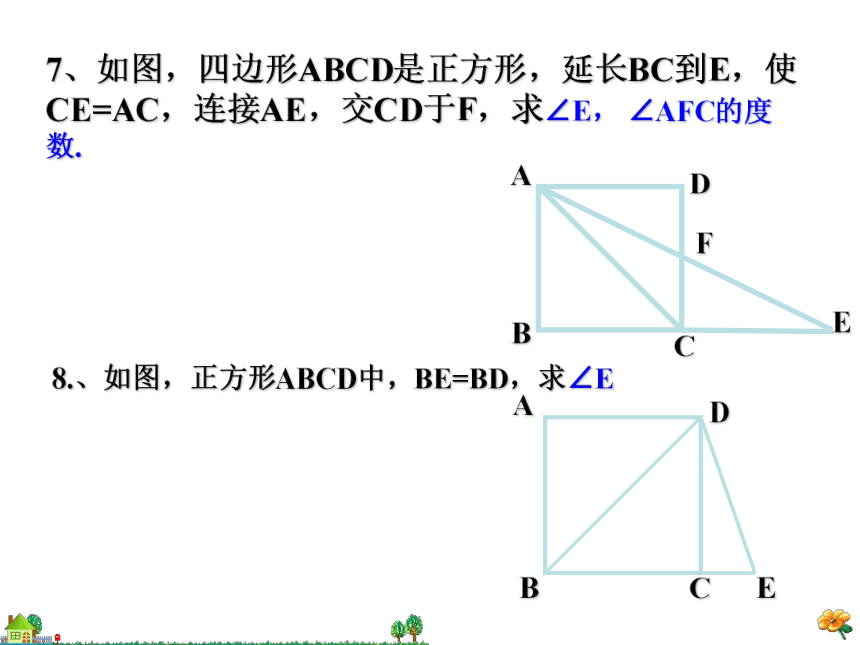
7、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠E, ∠AFC的度数.
A
B
D
C
E
F
8.、如图,正方形ABCD中,BE=BD,求∠E
A
B
C
D
E
练:正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
课堂练习
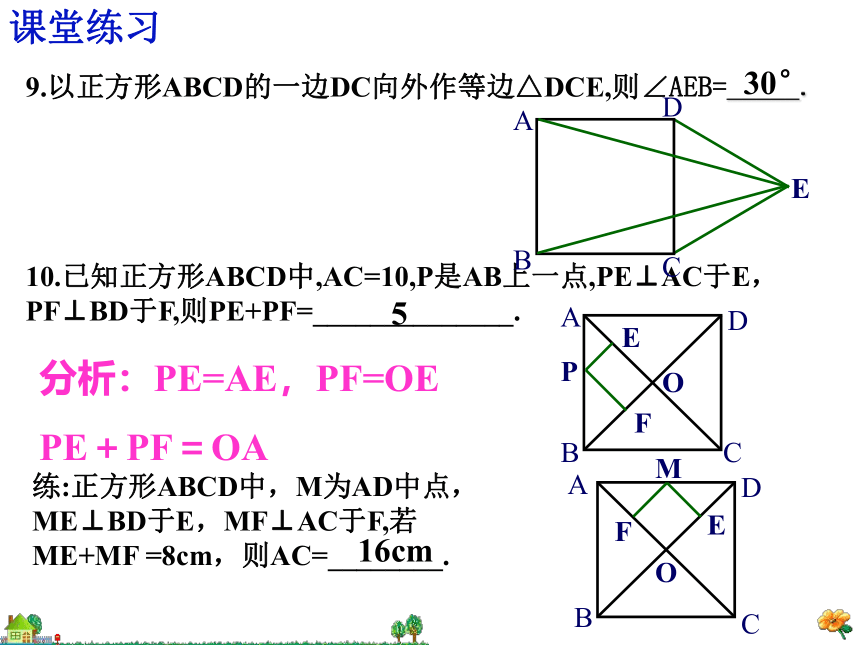
10.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
30°
16cm
9.以正方形ABCD的一边DC向外作等边△DCE,则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
M
A
B
C
D
E
F
O
分析:PE=AE,PF=OE
PE+PF=OA
11. 如图,在正方ABCD中,对角线AC、BD相交于O,
1)图中有多少个等腰直角三角形
2)说出图中相等的线段、相等的角。
3)求∠ABD、∠DAC、∠DOC的度数。
O
A
B
C
D
答案:1、八个 △ABC△BCD △CDA △DAB △AOB △AOD △BOC △COD
2 AB=BC=CD=DA AC=BD
OA=OB=OC=OD
3答案见课本107页
12.如图四边形ABCD和DEFG都是正方形,试说明AE=CG
解:
因为四边形ABCD是正方形
根据正方形的四边相等,得
AD=CD
又知四边形DEFG也是正方形
所以 DE=DG
又因为正方形的每个内角为90°
所以∠ADE+∠EDC=∠CDG+∠EDC
所以∠ADE=∠CDG
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD
所以AE=CG
A
B
C
D
E
F
G
13:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:(1)AE=AF;(2)EA⊥AF.
1
2
3
证明:(1)∵ ABCD是正方形
∴AD=AB,∠ADE=∠ABF=90°
在△ABF与△ADC中
AD=AB
∠ADE=∠ABF=90°
DE=BF
∴ △ABF≌△ADE(SAS)
∴ FA=EA ,∠1=∠3
(2)∵∠2+∠3=90 °
∴∠1+∠2=90 °
∴ EA⊥FA
1
2
3
14.如图,正方形ABCD中,点E是CD边上一点,连接AE交对角线BD于点F,则图中全等三角形共有( )
A B
C D
E
F
C
A.1对
B.2对
C.3对
D.4对
15.如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
16.如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两
正方形重合部分的
面积是
A D
B C
O
P
Q
R
17、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,
猜想AE与CG的位置
关系,并证明你的
猜想。
A
B D E
C
G F
18、正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.
A
B
C
D
E
F
若∠DCE=30°则∠DAF=
19、(1)边长为2cm 的正方形,对角线的长是______cm
A
B
C
D
O
(2)正方形ABCD,对角线AC、BD相交于点O,问图中有____个等腰直角三角形
解:以正方形的四个顶点为直角顶点,共有四个等腰直角三角形,以正方形两条对角线的交点为顶点的等腰直角三角形也有四个,因而共有八个等到腰直角三角形.分别是:
8
20、如图,将一张长方形纸对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
只要保证剪口线与折痕成45°角即可
B
C
D
O
解: ∵正方形ABCD是菱形.
∴AC ⊥BD
∴ ∠AOB= 90°
又 ∵正方形ABCD既是矩形又是菱形.
∴ ∠BAD= 90°, 且AC平分∠BAD
∴ ∠OAB= 45°
例1:如图,四边形ABCD是正方形,两条对角线相交于点O,求∠AOB,∠OAB的度数。
例2:正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
解:
∵正方形ABCD的四个角均为直角,且对角线平分一组对角。
∵CE=AC
∴∠E=∠CAE
∵∠ACB是⊿ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是⊿CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
j
F
E
A
B
D
C
例3:如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF
A
B
C
D
P
E
F
解:
连接PC
∵PE⊥BC , PF⊥DC
而四边形ABCD是正方形
∴∠FCE=90°
∴四边形PECF是矩形
∴PC=EF
又∵四边形BAPC是以BD为轴的轴对称图形
∴AP=PC
∴AP=EF
小试牛刀
1.正方形ABCD,对角线交于0,
1)若AB=2㎝,则AC=_____,OA=_____,周长____,面积_____。
2)若OB=2㎝,则AC=_____,AB=_____,周长____,面积_____。
3)若AC+BD=8㎝,则AC=_____,AB=_____,正方形面积_____。
2.已知正方形的面积为9cm,它的周长为 _______________.
3.正方形的边长为a,当边长增加1时,其面积增加了__________.
O
A
B
C
D
4.正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
5.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
随堂练习
用10米长的篱笆围成一个四边形菜地,如何确定面积最大的四边形的形状,面积为多少?
在长度给定的情况下,围成的四边形中,
正方形的面积最大。
6.
7、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠E, ∠AFC的度数.
A
B
D
C
E
F
8.、如图,正方形ABCD中,BE=BD,求∠E
A
B
C
D
E
练:正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
课堂练习
10.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
30°
16cm
9.以正方形ABCD的一边DC向外作等边△DCE,则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
M
A
B
C
D
E
F
O
分析:PE=AE,PF=OE
PE+PF=OA
11. 如图,在正方ABCD中,对角线AC、BD相交于O,
1)图中有多少个等腰直角三角形
2)说出图中相等的线段、相等的角。
3)求∠ABD、∠DAC、∠DOC的度数。
O
A
B
C
D
答案:1、八个 △ABC△BCD △CDA △DAB △AOB △AOD △BOC △COD
2 AB=BC=CD=DA AC=BD
OA=OB=OC=OD
3答案见课本107页
12.如图四边形ABCD和DEFG都是正方形,试说明AE=CG
解:
因为四边形ABCD是正方形
根据正方形的四边相等,得
AD=CD
又知四边形DEFG也是正方形
所以 DE=DG
又因为正方形的每个内角为90°
所以∠ADE+∠EDC=∠CDG+∠EDC
所以∠ADE=∠CDG
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD
所以AE=CG
A
B
C
D
E
F
G
13:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:(1)AE=AF;(2)EA⊥AF.
1
2
3
证明:(1)∵ ABCD是正方形
∴AD=AB,∠ADE=∠ABF=90°
在△ABF与△ADC中
AD=AB
∠ADE=∠ABF=90°
DE=BF
∴ △ABF≌△ADE(SAS)
∴ FA=EA ,∠1=∠3
(2)∵∠2+∠3=90 °
∴∠1+∠2=90 °
∴ EA⊥FA
1
2
3
14.如图,正方形ABCD中,点E是CD边上一点,连接AE交对角线BD于点F,则图中全等三角形共有( )
A B
C D
E
F
C
A.1对
B.2对
C.3对
D.4对
15.如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
16.如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两
正方形重合部分的
面积是
A D
B C
O
P
Q
R
17、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,
猜想AE与CG的位置
关系,并证明你的
猜想。
A
B D E
C
G F
18、正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.
A
B
C
D
E
F
若∠DCE=30°则∠DAF=
19、(1)边长为2cm 的正方形,对角线的长是______cm
A
B
C
D
O
(2)正方形ABCD,对角线AC、BD相交于点O,问图中有____个等腰直角三角形
解:以正方形的四个顶点为直角顶点,共有四个等腰直角三角形,以正方形两条对角线的交点为顶点的等腰直角三角形也有四个,因而共有八个等到腰直角三角形.分别是:
8
20、如图,将一张长方形纸对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
只要保证剪口线与折痕成45°角即可
