人教版初中数学八年级下册18.1.2《平行四边形的判定(二)》课件(共19张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册18.1.2《平行四边形的判定(二)》课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:59:11 | ||
图片预览




文档简介
【知识与能力】
系统掌握平行四边形的判定定理;
灵活运用判定定理进行有关判断和说理叙述.
【过程与方法】
通过平行四边形判定定理的归纳与说理,培养的归纳推理能力,领会数学的严密性;
通过尝试练习和变式尝试,培养分析问题和解决问题的能力.
【情感态度与价值观】
通过平行四边形判定方法的灵活运用,培养主动探索的精神及创新意识;
通过一题多变与一题多解,引发求异创新的欲望.
教学目标
18.1.2 平行四边形的判定
重点:
平行四边形的判定方法及应用.
难点:
平行四边形的判定定理与性质定理的灵活应用.
课时:
计划四课时完成本大节内容.
教学重难点及课时安排
课前导入:
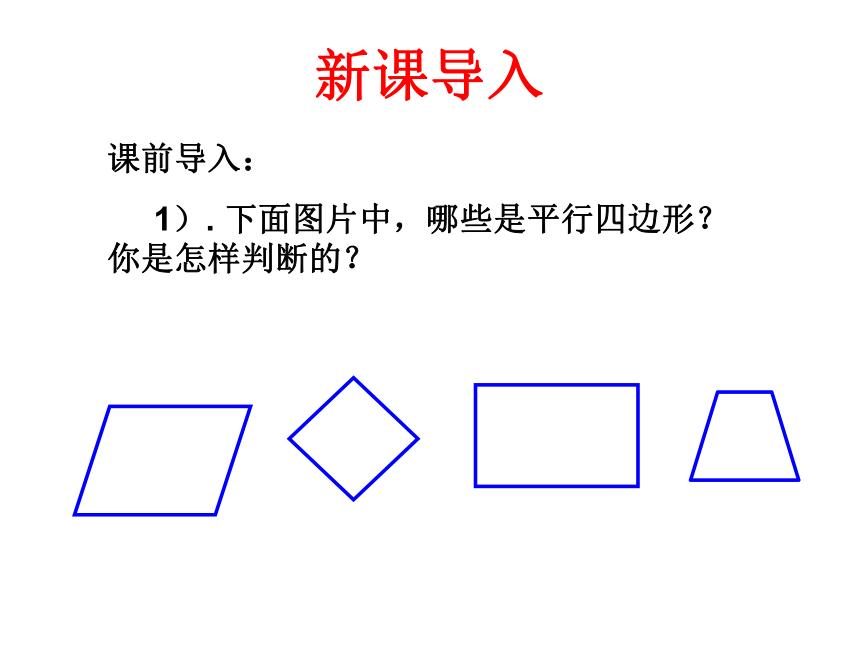
1). 下面图片中,哪些是平行四边形?你是怎样判断的?
新课导入
2).平行四边形的主要特征
1.边: a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
2.角:平行四边形两组对角分别相等.
3.对角线: 平行四边形对角线互相平分 .
怎样证明四
边形是不是平行四边形?
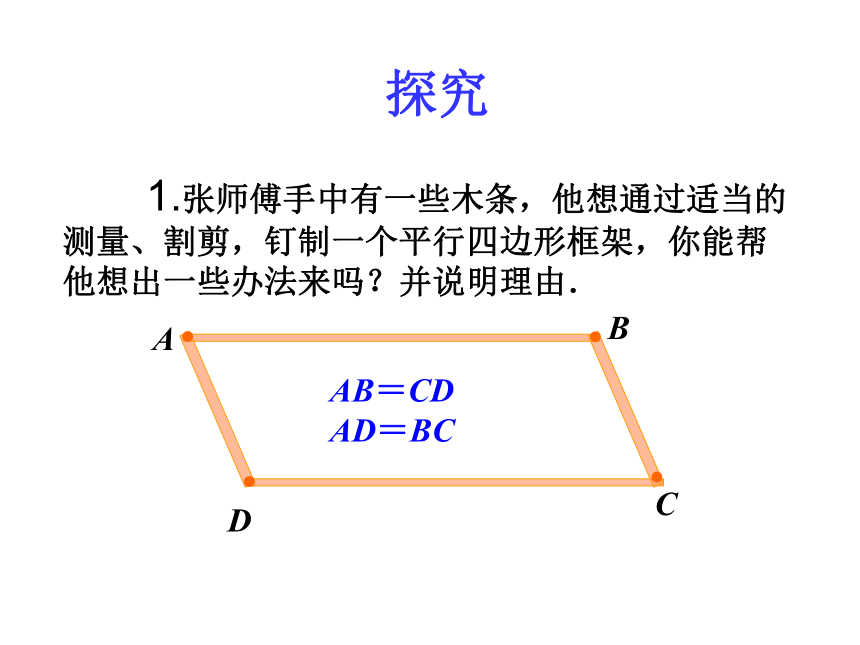
1.张师傅手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.
●
●
●
●
A
C
B
D
AB=CD
AD=BC
探究
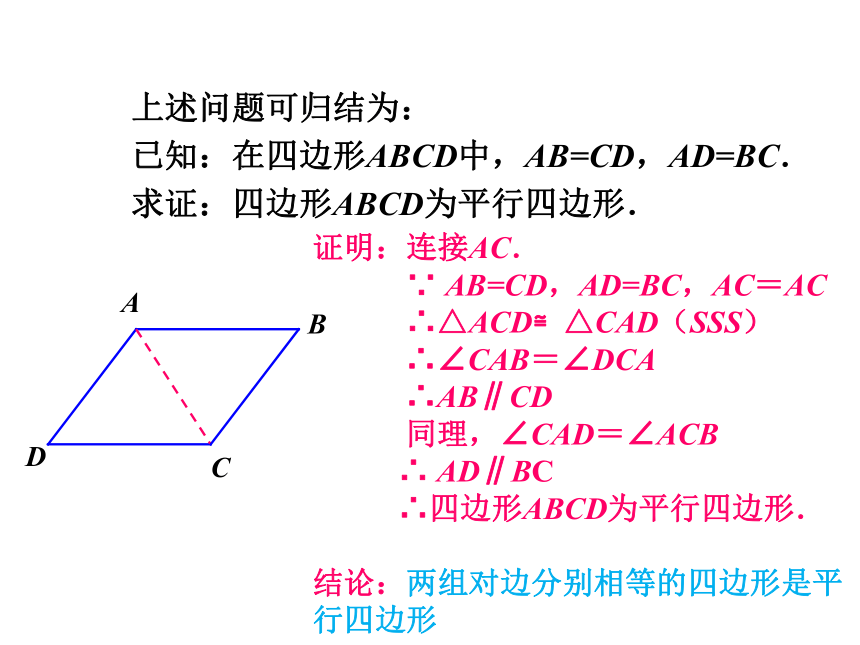
证明:连接AC.
∵ AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴ AD∥BC
∴四边形ABCD为平行四边形.
结论:两组对边分别相等的四边形是平行四边形
上述问题可归结为:
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形.
A
C
B
D
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
探究
△AOB≌△COD →
∠BAC=∠ACD→AB∥CD
∠CAD=∠ACB→AD∥BC
同理,△BOC≌△AOD →
四边形ABCD是平行四边形.
结论:两条对角线互相平分的四边形是平行四边形.
A
C
B
O
D
知识要点:
平行四边形判定方法1
两组对边分别相等的四边形是平行四边形.
平行四边形判定方法2
对角线互相平分的四边形是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,∠D=∠B.
∵ E,F分别是边AB,CD的中点,
∴BE=DF
∴△ADF≌△CBE
∴AF=CE
又∵AE=CF
∴四边形AECF是平行四边形.
A
F
E
D
C
B
【例1】已知: ABCD中,E,F分别是边AB,CD的中点,求证:四边形AECF是平行四边形.
D
F
E
C
B
A
O
1. 如下图 , ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于点E,F.连接EB,EC.求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD∥BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形.
证明:作对角线BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ BO=DO OA=OC
又∵ EA=FC
∴OE=OF
∴ 四边形BFDE是平行四边形
2. 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
O
D
A
B
C
E
F
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
证明:连接对角线BD,交AC于点O
【例】已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
还有其他证明方法吗?请同学们想一想?
AE=CF
∠EAD=∠FCB
AD=BC
D
A
B
C
E
F
证明:∵四边形ABCD是平行四边形
∴AD ∥ BC且AD =BC
∴∠EAD=∠FCB
在△AED和△CFB中
∴△AED ≌△CFB(SAS)
∴DE=BF
同理可证:BE=DF
四边形BFDE是平行四边形.
变式:1.已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?
D
A
B
C
E
F
O
2.已知:如图,A′B′∥BA,B′C′∥CB,
C′A′∥AC.
求证:
(1) ∠ABC=∠B′, ∠CAB=∠A′,
∠BCA=∠C′;
(2) △ABC的顶点分别是△B′C′A′各边的
中点.
A
C
B
A′
C′
B′
证明:(1) ∵ A′B′∥BA,C′B′∥BC,
∴ 四边形ABCB′是平行四边形.
∴ ∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.
(2) 由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形.
∴ AB=B′C, AB=A′C(平行四边形的对边相等).
∴ B′C=A′C.
同理 B′A=C′A, A′B=C′B.
∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点.
小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由.
A
B
C
D
O
F
E
系统掌握平行四边形的判定定理;
灵活运用判定定理进行有关判断和说理叙述.
【过程与方法】
通过平行四边形判定定理的归纳与说理,培养的归纳推理能力,领会数学的严密性;
通过尝试练习和变式尝试,培养分析问题和解决问题的能力.
【情感态度与价值观】
通过平行四边形判定方法的灵活运用,培养主动探索的精神及创新意识;
通过一题多变与一题多解,引发求异创新的欲望.
教学目标
18.1.2 平行四边形的判定
重点:
平行四边形的判定方法及应用.
难点:
平行四边形的判定定理与性质定理的灵活应用.
课时:
计划四课时完成本大节内容.
教学重难点及课时安排
课前导入:
1). 下面图片中,哪些是平行四边形?你是怎样判断的?
新课导入
2).平行四边形的主要特征
1.边: a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
2.角:平行四边形两组对角分别相等.
3.对角线: 平行四边形对角线互相平分 .
怎样证明四
边形是不是平行四边形?
1.张师傅手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.
●
●
●
●
A
C
B
D
AB=CD
AD=BC
探究
证明:连接AC.
∵ AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴ AD∥BC
∴四边形ABCD为平行四边形.
结论:两组对边分别相等的四边形是平行四边形
上述问题可归结为:
已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD为平行四边形.
A
C
B
D
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
探究
△AOB≌△COD →
∠BAC=∠ACD→AB∥CD
∠CAD=∠ACB→AD∥BC
同理,△BOC≌△AOD →
四边形ABCD是平行四边形.
结论:两条对角线互相平分的四边形是平行四边形.
A
C
B
O
D
知识要点:
平行四边形判定方法1
两组对边分别相等的四边形是平行四边形.
平行四边形判定方法2
对角线互相平分的四边形是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC,∠D=∠B.
∵ E,F分别是边AB,CD的中点,
∴BE=DF
∴△ADF≌△CBE
∴AF=CE
又∵AE=CF
∴四边形AECF是平行四边形.
A
F
E
D
C
B
【例1】已知: ABCD中,E,F分别是边AB,CD的中点,求证:四边形AECF是平行四边形.
D
F
E
C
B
A
O
1. 如下图 , ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于点E,F.连接EB,EC.求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD∥BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形.
证明:作对角线BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ BO=DO OA=OC
又∵ EA=FC
∴OE=OF
∴ 四边形BFDE是平行四边形
2. 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
O
D
A
B
C
E
F
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
证明:连接对角线BD,交AC于点O
【例】已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
还有其他证明方法吗?请同学们想一想?
AE=CF
∠EAD=∠FCB
AD=BC
D
A
B
C
E
F
证明:∵四边形ABCD是平行四边形
∴AD ∥ BC且AD =BC
∴∠EAD=∠FCB
在△AED和△CFB中
∴△AED ≌△CFB(SAS)
∴DE=BF
同理可证:BE=DF
四边形BFDE是平行四边形.
变式:1.已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?
D
A
B
C
E
F
O
2.已知:如图,A′B′∥BA,B′C′∥CB,
C′A′∥AC.
求证:
(1) ∠ABC=∠B′, ∠CAB=∠A′,
∠BCA=∠C′;
(2) △ABC的顶点分别是△B′C′A′各边的
中点.
A
C
B
A′
C′
B′
证明:(1) ∵ A′B′∥BA,C′B′∥BC,
∴ 四边形ABCB′是平行四边形.
∴ ∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.
(2) 由(1)证得四边形ABCB′是平行四边形.同理,四边形ABA′C是平行四边形.
∴ AB=B′C, AB=A′C(平行四边形的对边相等).
∴ B′C=A′C.
同理 B′A=C′A, A′B=C′B.
∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点.
小明用手中六个全等的正三角形做拼图游戏时,拼成一个六边形.你能在图中找出所有的平行四边形吗?并说说你的理由.
A
B
C
D
O
F
E
