人教版初中数学七年级下册第八章8.2消元解二元一次方程组优质课件(共35张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册第八章8.2消元解二元一次方程组优质课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览











文档简介
3.已知二元一次方程3x-2y=9,若y=0,则x= 。
{
x=-2
y=3
4. 若
是x-ky=1的解,则k= .
3
-1
复习回顾
1、什么叫二元一次方程?二元一次方程组?二元一次方程组的解?
2、检验二元一次方程组的解的方法是怎样的?
6.已知二元一次方程2X+3Y+5=0
⑴用X表示Y ⑵用Y表示X
5.下列各式是二元一次方程的是( )
A. x=3y B. 2x+y=3z
C. x?+x-y=0 D. 3X+2=5
A
采取哪些步骤取决于要解什么形式的方程,各种步骤都是使方程向x=a形式转化。
—— 看括号前的符号以确定括号内各项是否变号
解一元一次方程的步骤:
(1)去分母
(2)去括号
(3)移项
(4)合并
(5)系数化为1
—— 防漏乘
—— 要变号
思考
x+y=7
5x+3y=27
如何求出方程组
的解?
对于一元一次方程的求解,我们已经很熟悉了,所以如果能把二元一次方程组转化为一元一次方程,就能求出该方程组的解。
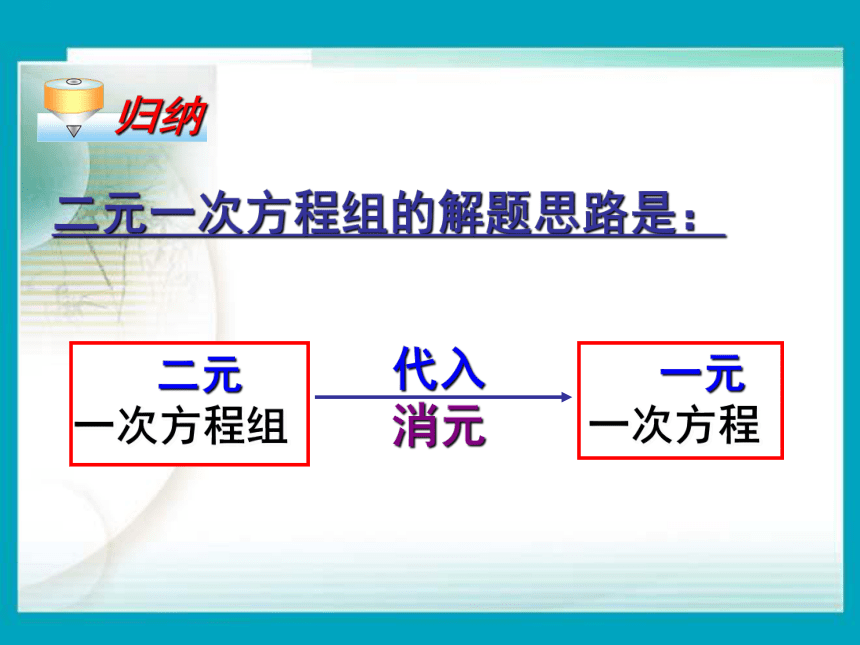
二元一次方程组中有两个未知数,如果消去其中一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程,我们就可以先解出一个未知数,然后再设法求另一个未知数。这种将未知数的个数由多化为少、逐一解决的想法,叫做消元思想。
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。
归纳
解方程组:
x+2y=11 ①
5x+3y=27 ②
探究
解:由①得 x=11-2y ③
把③代入②,得
5(11-2y)+3y=27
-7y=-28
y=4
x=3
y=4
所以原方程组的解为
x=3
55-10y+3y=27
把y=4代入方程③,得:
分析:方程①中x的系数是1,用含y的式子表示x,比较简便。
代入
消元
二元一次方程组的解题思路是:
二元 一次方程组
一元 一次方程
归纳
x+1=2(y-1)
①
②
解:由①得,y=x-2 ③
x+1=2(x-2-1)
x=7
再把x=7代入③,得y=5
所以原方程组的解为
x-y=2
x=7 y=5
试一试
把③代入②,得
1、解方程组:
D
2.用代入法解方程组
3X+4Y=2
2X-Y=5
①
②
使得代入后化简比较容易的变形是:( )
A 由①得
C 由②得
D 由②得
Y=2X-5
B 由①得Y=
1、把下列方程写成用含x的代数式表示y的形式:
(1)3x+4y-1=0
(2)5x-2y+9=0
解:
y=
1-3x
4
y=
5x+9
2
(1)
(2)
练习
2、解方程组:
解:由②得:
y=17-3x
③
把③代入①得
2x+3(17-3x)=16
解得 x=5
把x=5代入③得
y=2
所以原方程组的解为
y=2
x=5
①
3x+y=17
2x+3y=16
②
由①直接代入②
下列各方程组中,应怎样代入消元?
由①得y=7x –11 ③
将③代入②
x=4y-1 ①
3x +y=10 ②
7x-y=11 ①
5x +2y=0 ②
探究
由①得:8y=4-2x③
将③代入②
由①得:9x=4+11y③
将③代入②
2x+8y=4 ①
5x -8y+1=0 ②
9x-11y=4 ①
9x -8y+2=0 ②
你有什么发现?
用代入法时,往往对方程组中系数为1的未知数所在的方程进行变形代入。
(1)将方程组中未知数系数为1的方程变形,用一个未知数的代数式表示系数为1的未知数;
(2)将变形后的方程代入另一个方程消去一个未知数得一个一元一次方程;
(3)解这个一元一次方程求出一个未知数的值;
(4)把求得的未知数的值代入变形好的方程中,即可得另一个未知数的值;
(5)作答。
代入消元法一般步骤:
若 与 的和仍是单项式,求 的值.
解:由题意得:
m-3n=8
5m+n=8
n= - 2
m=2
解得:
所以
m+n=2+(-2)=0
综合运用
用代入法消元,需找出方程组中系数为1的未知数,但此方程组中未知数的系数都不为1,直接用代入法计算难度较大。你能想到更好的方法解吗?
4x+10y=18
15x-10y=20
如何求出方程组
的解?
仔细观察,这个方程组有什么特点?
4 x + 10y =18
15x - 10y =20
思考
方程①中的+10y与方程②中的-10y系数相反,若两方程两边分别相加,就能消去未知数y。也就达到了消元的目的.
现在你会解这个方程组了吗?
①
②
解:①+②得:
4x+10y+15x-10y=18+20
19x=38
把x=2代入① ,得y=1
所以原方程组的解为
4x+10y=18
15x-10y=20
x=2
y=1
x=2
探究
2x+5y=19
2x+3y=13
解方程组
观察方程组,你发现了什么?怎样才能消元?
方程①中的2x与方程②中的2x系数相同,若两方程两边分别相减,就能消去未知数x。也就达到了消元的目的.
现在你会解这个方程组了吗?
①
②
解:①-②得:
2x+5y -(2x+3y)=19-13
2y=6
把y=3代入① ,得x=2
所以原方程组的解为
y=3
y=3
x=2
2x+5y=19
2x+3y=13
2x+5y -2x-3y =6
两个二元一次方程中同一个未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法。
归纳
练习
解方程组
解:①-②,得
代入②,得
把
所以原方程组的解为
①
②
小结
两个二元一次方程中同一个未知数的系数相反或相等,即为同一未知数系数的绝对值相等。故同一未知数系数的绝对值相等时,就可以用加减消元法求出方程组的解。
还有没有其他形式也可以用加减消元的呢?
思考
1、解方程组
分析:方程中同一未知数的系数都不为1,不适合用代入法消元;而且同一未知数的系数的绝对值也不相等,直接加减两个方程不能消元。试一试,能否对方程变形,使得两个方程中某个未知数的系数相反或相同?
①
②
方程中同一未知数的系数有倍数关系,则可以通过扩大相应的倍数,使得同一未知数的系数相同或相反。
解方程组
9x+12y =30 ③
10y=15
把y=1.5代入① ,得x=
所以原方程组的解为
y=1.5
12y -2y =30-15
解:②×3,得:
③- ①,得:
y=1.5
x=
①
②
3x+4y=16
5x-6y=33
①
②
2、解方程组
解: ① ×3,得:
19x=114
把x=6代入① ,得y=-0.5
所以原方程组的解为
x=6
②×2, 得:
③ + ④ ,得:
9x+12y=48 ③
10x-12y=66 ④
y=-0.5
x=6
如果两个方程中,未知数系数的绝对值都不相等,可以在方程两边都乘以同一个适当的数,使两个方程中有一个未知数的系数绝对值相等,然后再加减消元.
归纳
用加减法解二元一次方程组的步骤:
(1) 方程组的两个方程中,若同一个未知数的系数绝对值相当,则可以直接加减消元;如果同一个未知数的系数绝对值不相等,就用适当的数去乘方程的两边,使一个未知数的系数绝对值相等;
(2) 加减消元,得到一个一元一次方程;
(3) 解这个一元一次方程;
(4) 将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.
判断
下列方程组适合选择哪种方法消元?
3m+n=11
-4m-n=11
4a+b=15
3b-4a=-3
x-y=4
4x+2y=-1
5x-y=110
9y-x=110
代入消元法
加减消元法
加减消元法
加减消元法
代入消元法
加减消元法
⑴方程5X-3Y=7,变形可得X=_________,Y=__________.
⑵解方程组
y=x-3 ①
2x+3y=6 ②
应消去____,可把_____代入_____.
⑶方程y=2x-3和方程3x+2y=1的公共解是
x=_____
y=_____
y
①
②
1
-1
巩固练习
⑸若 是方程组
的解,求k和m的值。
x=2
y=1
kx-my=1
mx+ky=8
(4)|x+y-2|+(2x-3y+5)2=0,求x和y的值。
试一试
{
x=-2
y=3
4. 若
是x-ky=1的解,则k= .
3
-1
复习回顾
1、什么叫二元一次方程?二元一次方程组?二元一次方程组的解?
2、检验二元一次方程组的解的方法是怎样的?
6.已知二元一次方程2X+3Y+5=0
⑴用X表示Y ⑵用Y表示X
5.下列各式是二元一次方程的是( )
A. x=3y B. 2x+y=3z
C. x?+x-y=0 D. 3X+2=5
A
采取哪些步骤取决于要解什么形式的方程,各种步骤都是使方程向x=a形式转化。
—— 看括号前的符号以确定括号内各项是否变号
解一元一次方程的步骤:
(1)去分母
(2)去括号
(3)移项
(4)合并
(5)系数化为1
—— 防漏乘
—— 要变号
思考
x+y=7
5x+3y=27
如何求出方程组
的解?
对于一元一次方程的求解,我们已经很熟悉了,所以如果能把二元一次方程组转化为一元一次方程,就能求出该方程组的解。
二元一次方程组中有两个未知数,如果消去其中一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程,我们就可以先解出一个未知数,然后再设法求另一个未知数。这种将未知数的个数由多化为少、逐一解决的想法,叫做消元思想。
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。
归纳
解方程组:
x+2y=11 ①
5x+3y=27 ②
探究
解:由①得 x=11-2y ③
把③代入②,得
5(11-2y)+3y=27
-7y=-28
y=4
x=3
y=4
所以原方程组的解为
x=3
55-10y+3y=27
把y=4代入方程③,得:
分析:方程①中x的系数是1,用含y的式子表示x,比较简便。
代入
消元
二元一次方程组的解题思路是:
二元 一次方程组
一元 一次方程
归纳
x+1=2(y-1)
①
②
解:由①得,y=x-2 ③
x+1=2(x-2-1)
x=7
再把x=7代入③,得y=5
所以原方程组的解为
x-y=2
x=7 y=5
试一试
把③代入②,得
1、解方程组:
D
2.用代入法解方程组
3X+4Y=2
2X-Y=5
①
②
使得代入后化简比较容易的变形是:( )
A 由①得
C 由②得
D 由②得
Y=2X-5
B 由①得Y=
1、把下列方程写成用含x的代数式表示y的形式:
(1)3x+4y-1=0
(2)5x-2y+9=0
解:
y=
1-3x
4
y=
5x+9
2
(1)
(2)
练习
2、解方程组:
解:由②得:
y=17-3x
③
把③代入①得
2x+3(17-3x)=16
解得 x=5
把x=5代入③得
y=2
所以原方程组的解为
y=2
x=5
①
3x+y=17
2x+3y=16
②
由①直接代入②
下列各方程组中,应怎样代入消元?
由①得y=7x –11 ③
将③代入②
x=4y-1 ①
3x +y=10 ②
7x-y=11 ①
5x +2y=0 ②
探究
由①得:8y=4-2x③
将③代入②
由①得:9x=4+11y③
将③代入②
2x+8y=4 ①
5x -8y+1=0 ②
9x-11y=4 ①
9x -8y+2=0 ②
你有什么发现?
用代入法时,往往对方程组中系数为1的未知数所在的方程进行变形代入。
(1)将方程组中未知数系数为1的方程变形,用一个未知数的代数式表示系数为1的未知数;
(2)将变形后的方程代入另一个方程消去一个未知数得一个一元一次方程;
(3)解这个一元一次方程求出一个未知数的值;
(4)把求得的未知数的值代入变形好的方程中,即可得另一个未知数的值;
(5)作答。
代入消元法一般步骤:
若 与 的和仍是单项式,求 的值.
解:由题意得:
m-3n=8
5m+n=8
n= - 2
m=2
解得:
所以
m+n=2+(-2)=0
综合运用
用代入法消元,需找出方程组中系数为1的未知数,但此方程组中未知数的系数都不为1,直接用代入法计算难度较大。你能想到更好的方法解吗?
4x+10y=18
15x-10y=20
如何求出方程组
的解?
仔细观察,这个方程组有什么特点?
4 x + 10y =18
15x - 10y =20
思考
方程①中的+10y与方程②中的-10y系数相反,若两方程两边分别相加,就能消去未知数y。也就达到了消元的目的.
现在你会解这个方程组了吗?
①
②
解:①+②得:
4x+10y+15x-10y=18+20
19x=38
把x=2代入① ,得y=1
所以原方程组的解为
4x+10y=18
15x-10y=20
x=2
y=1
x=2
探究
2x+5y=19
2x+3y=13
解方程组
观察方程组,你发现了什么?怎样才能消元?
方程①中的2x与方程②中的2x系数相同,若两方程两边分别相减,就能消去未知数x。也就达到了消元的目的.
现在你会解这个方程组了吗?
①
②
解:①-②得:
2x+5y -(2x+3y)=19-13
2y=6
把y=3代入① ,得x=2
所以原方程组的解为
y=3
y=3
x=2
2x+5y=19
2x+3y=13
2x+5y -2x-3y =6
两个二元一次方程中同一个未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法。
归纳
练习
解方程组
解:①-②,得
代入②,得
把
所以原方程组的解为
①
②
小结
两个二元一次方程中同一个未知数的系数相反或相等,即为同一未知数系数的绝对值相等。故同一未知数系数的绝对值相等时,就可以用加减消元法求出方程组的解。
还有没有其他形式也可以用加减消元的呢?
思考
1、解方程组
分析:方程中同一未知数的系数都不为1,不适合用代入法消元;而且同一未知数的系数的绝对值也不相等,直接加减两个方程不能消元。试一试,能否对方程变形,使得两个方程中某个未知数的系数相反或相同?
①
②
方程中同一未知数的系数有倍数关系,则可以通过扩大相应的倍数,使得同一未知数的系数相同或相反。
解方程组
9x+12y =30 ③
10y=15
把y=1.5代入① ,得x=
所以原方程组的解为
y=1.5
12y -2y =30-15
解:②×3,得:
③- ①,得:
y=1.5
x=
①
②
3x+4y=16
5x-6y=33
①
②
2、解方程组
解: ① ×3,得:
19x=114
把x=6代入① ,得y=-0.5
所以原方程组的解为
x=6
②×2, 得:
③ + ④ ,得:
9x+12y=48 ③
10x-12y=66 ④
y=-0.5
x=6
如果两个方程中,未知数系数的绝对值都不相等,可以在方程两边都乘以同一个适当的数,使两个方程中有一个未知数的系数绝对值相等,然后再加减消元.
归纳
用加减法解二元一次方程组的步骤:
(1) 方程组的两个方程中,若同一个未知数的系数绝对值相当,则可以直接加减消元;如果同一个未知数的系数绝对值不相等,就用适当的数去乘方程的两边,使一个未知数的系数绝对值相等;
(2) 加减消元,得到一个一元一次方程;
(3) 解这个一元一次方程;
(4) 将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.
判断
下列方程组适合选择哪种方法消元?
3m+n=11
-4m-n=11
4a+b=15
3b-4a=-3
x-y=4
4x+2y=-1
5x-y=110
9y-x=110
代入消元法
加减消元法
加减消元法
加减消元法
代入消元法
加减消元法
⑴方程5X-3Y=7,变形可得X=_________,Y=__________.
⑵解方程组
y=x-3 ①
2x+3y=6 ②
应消去____,可把_____代入_____.
⑶方程y=2x-3和方程3x+2y=1的公共解是
x=_____
y=_____
y
①
②
1
-1
巩固练习
⑸若 是方程组
的解,求k和m的值。
x=2
y=1
kx-my=1
mx+ky=8
(4)|x+y-2|+(2x-3y+5)2=0,求x和y的值。
试一试
