人教版七年级数学下册 第七章平面直角坐标系复习 (20张PPT)
文档属性
| 名称 | 人教版七年级数学下册 第七章平面直角坐标系复习 (20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览




文档简介
第七章平面直角坐标系
学
习
目
标
1、认识平面直角坐标系,了解点与坐标的对应关系;
2、能在方格纸中建立适当的平面直角坐标系描述物体的位置,体会平面直角坐标系在解决实际问题中的作用;
3、能用坐标表示平移变换,通过研究平移与坐标关系,使学生看到平面直角坐标系是数与形之间的桥梁。
重、难点:会灵活运用平面直角坐标系的知识点解决问题
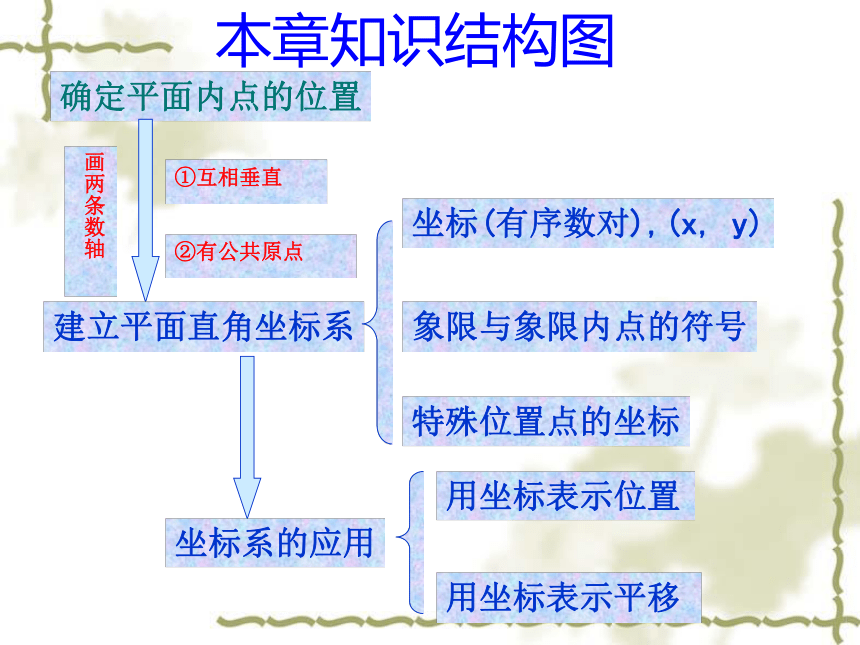
本章知识结构图
确定平面内点的位置
画两条数轴
①互相垂直
②有公共原点
建立平面直角坐标系
坐标(有序数对),(x,
y)
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示位置
用坐标表示平移
有序数对
一、有序数对的概念:
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对,记作(a
,
b).
理解有序数对时注意:
(1)不能随意交换两个数的位置。(3,5)和(5,3)表示不同的两个个位置。
(2)两个数组成的有序数对是个整体,不能分开。
5
可
明
个
万
女
4
中
我
的
一
学
3
爱
英
天
帅
活
2
球
里
是
生
大
1
小
孩
打
习
哥
A
B
C
D
E
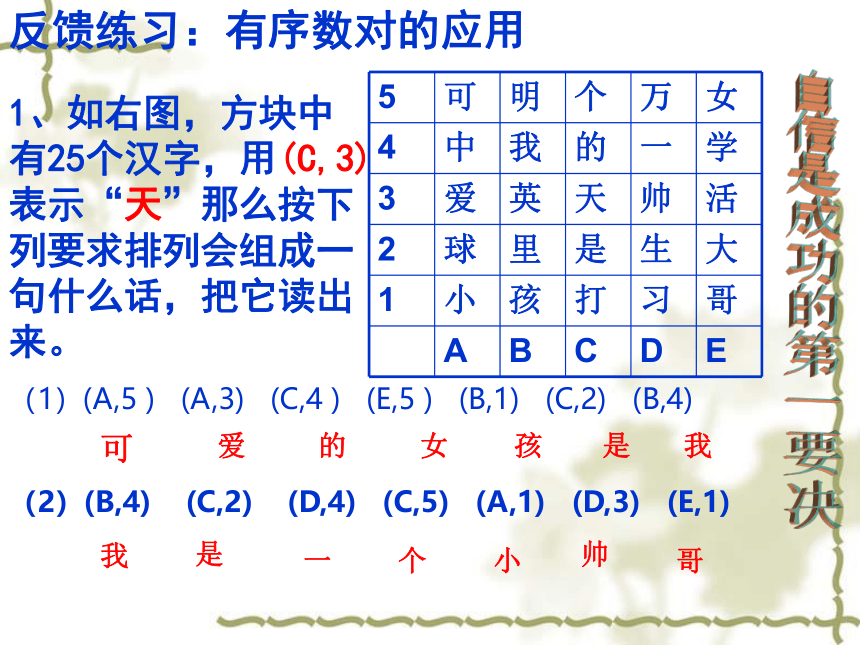
1、如右图,方块中有25个汉字,用(C,3)表示“天”那么按下列要求排列会组成一句什么话,把它读出来。
(1)(A,5
)
(A,3)
(C,4
)
(E,5
)
(B,1)
(C,2)
(B,4)
(2)(B,4)
(C,2)
(D,4)
(C,5)
(A,1)
(D,3)
(E,1)
可
爱
的
女
孩
是
我
我
是
一
个
小
帅
哥
反馈练习:有序数对的应用
(3)确定小区中住户的位置必须有四个数据,分别为楼号a,单元号b,层数c和住户号d,即“a楼b单元c层d号。”
(4)区域定位法:绘出所在区域代号如B3,D5等。排球比赛队员场上的位置等。
生活中还有哪些确定位置的其他方法?
(1)如果全班同学站成一列做早操,现在教师想找某个同学,是否还需要用2个数据呢?
(2)多层电影院确定座位位置用两个数据够用吗?
必须有三个数据(a,b,c),其中a表示层数,b表示排号,c表示座号,即“a层b排c号”。
5
-2
-3
-4
-1
3
2
4
1
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
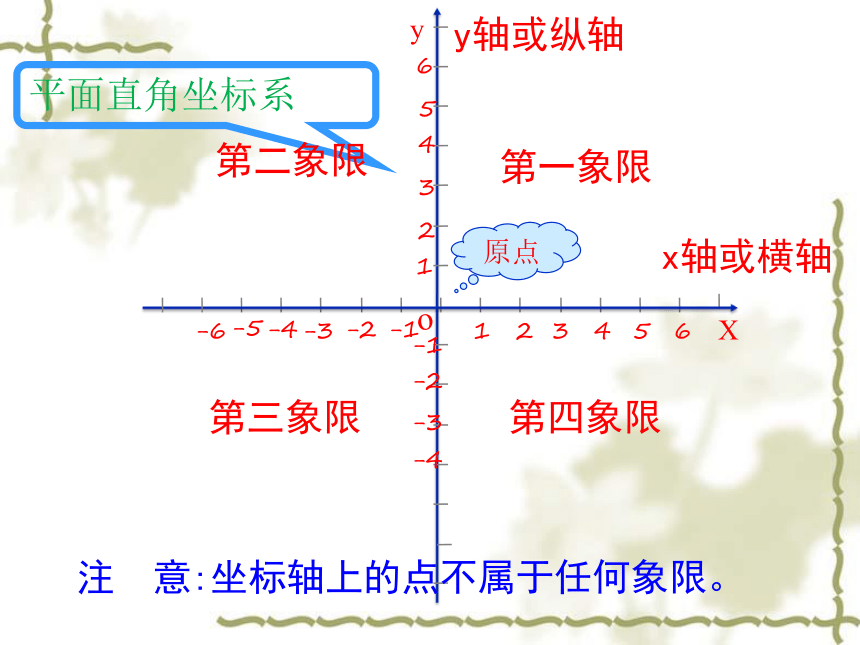
x轴或横轴
y轴或纵轴
原点
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注
意:坐标轴上的点不属于任何象限。
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
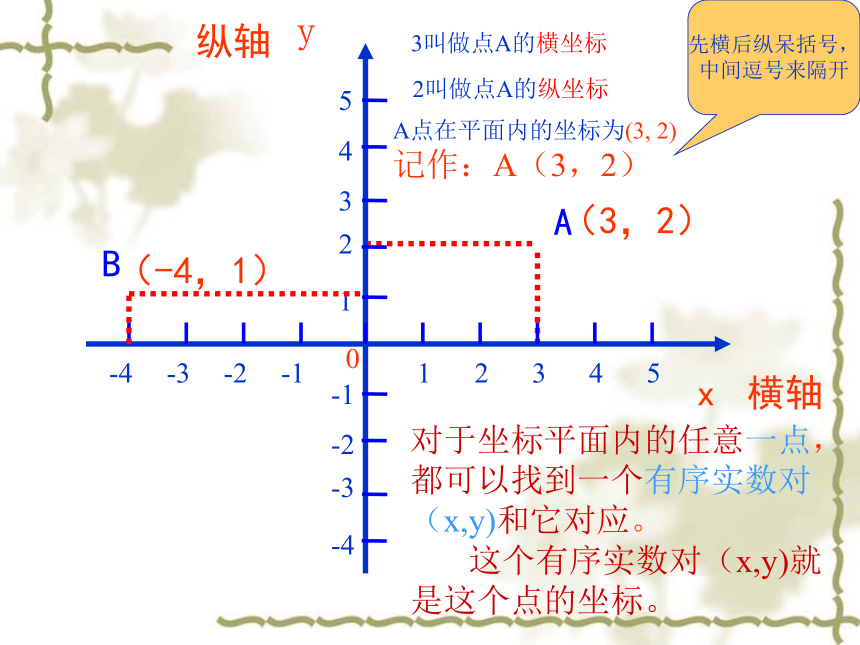
(3,2)
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3,
2)
记作:A(3,2)
先横后纵呆括号,
中间逗号来隔开
(-4,1)
B
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y)和它对应。
这个有序实数对(x,y)就是这个点的坐标。
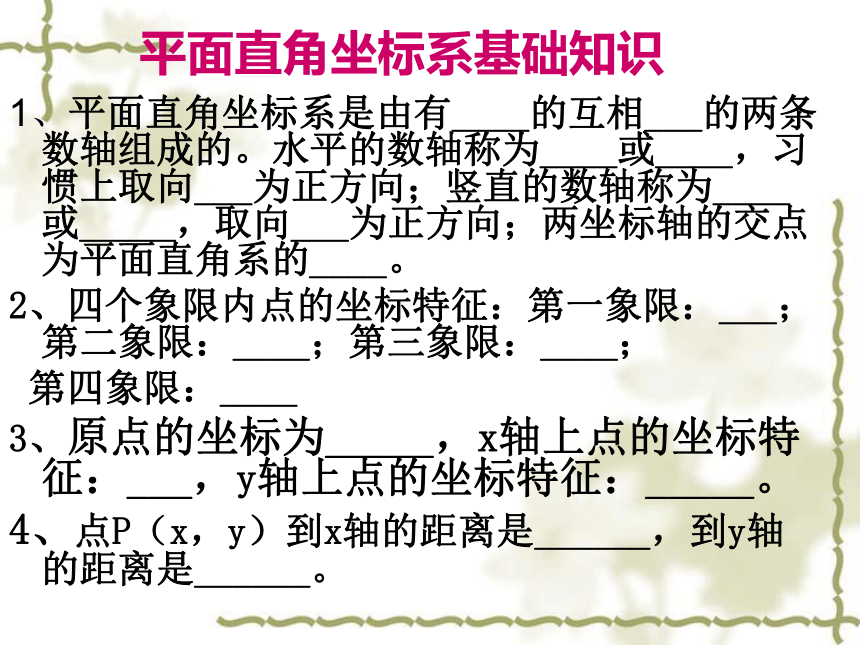
平面直角坐标系基础知识
1、平面直角坐标系是由有____的互相___的两条数轴组成的。水平的数轴称为____或____,习惯上取向___为正方向;竖直的数轴称为____或_____,取向___为正方向;两坐标轴的交点为平面直角系的____。
2、四个象限内点的坐标特征:第一象限:___;第二象限:____;第三象限:____;
第四象限:____
3、原点的坐标为_____,x轴上点的坐标特征:___,y轴上点的坐标特征:_____。
4、点P(x,y)到x轴的距离是______,到y轴的距离是______。
反馈练面直角坐标系的基础知识的运用
1、
已知坐标平面内点
P(a,a-b)在第四象限,那么点
Q(-a,b)
在
第____象限
2.如果点P(a+5,a?2)在y轴上,那么P点坐标为_____.
3.点A(?2,
-1)与x轴的距离是___;与y轴的距离是____.
4、点A在x轴上,距离原点4个单位长度,则A点的坐标是_____.
5、若点P在第二象限内,且到X轴和Y轴的距离分别是3和4,则点P的坐标为______.
(2)、如果两个点连线与x轴平行,那么这两个点的坐标有何特点?
如果两个点连线与y轴平行,那么这两个点的坐标有何特点?
0
1
1
x
y
A
B
C
D
E
F
G
H
(1)、每一个象限内的点的坐标在符号上有何特点?
研行(垂直)于坐标轴的直线上的点的坐标特征
知识要点:平行于x轴(垂直于Y轴)的直线上的点的____相同;平行于y轴(垂直于X轴)的直线上的点的_____相同。
反馈练习:
1、直线AB∥X轴,且点A(2,-3),若点B在坐标轴上,那么点B的坐标为_____
2、已知线段MN垂直于X轴,点M的坐标是(-1,3),若MN=4,则点N的坐标是_____.
研习三
角平分线上的点的坐标特征
知识要点:平面直角坐标系第一、三象限的角平分线上点的坐标特征_________,第二、四象限的角平分线上点的坐标特征________。
归纳:到坐标轴距离相等的点的坐标特征____
反馈练习:
1、
已知点P的坐标为(3a-2,a+6),且点P到两坐标轴距离相等,求a的值和P点坐标
研移和对称的点的坐标特征
知识要点:
1、点(x,y)向右或向左平移a个单位长度,可得到对应点_________或_________;点(x,y)向上或向下平移b个单位长度,可得到对应点_________或_________。
2、点M(a,b)关于x轴的对称点坐标是______,关于y轴的对称点是______,关于原点的对称点是_______
反馈练习
1、一只青蛙从点A(-1,0)处先向右跳2个单位长度,在向下跳2个单位长度到达B处,则B的坐标是____
2、线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标是______
3、点A
(4,-1)与点B关于X轴对称,则点B坐标是_____,AB=____
4、点O(x+y,2x+y)与点P(5,-10)关于Y轴对称,则点(x,y)坐标为______
研习五
两点间距离和面积的计算
知识要点:
1、在平面直角坐标系中,平行于坐标轴的直线上两点O(x,y)与P(a,b)
,OP=
_____
2、平面直角坐标系中,面积的计算,可以直接用公式计算,也可以借助三角形、长方形等特殊的图形和差来计算,计算时一定要看清楚图形的各边的长度
练习:1.点A(-5,0)点B(3,0),三角形ABC的面积是12,点C在Y轴上,求C点坐标;
变式:上题中C点若在X轴上或在X=3直线上,C点坐标怎样求?
1.已知:A(0,1),B(1,0),C(3,2).
(1)求△ABC的面积;
(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,直接写出点P坐标.
2、如右图
(1)将三角形ABC向左平移3格再向下平移2格后得到的三角形A1B1C1的坐标为___,三角形A1B1C1的面积是_____;
A
B
C
y
x
O
(2)在平面直角坐标系内是否存在一点D能使四边形ABCD构成平行四边形,若有请写出点D的坐标?
3:要修建一个平行四边形的花坛,
A(-3,2)、B
(-3
,-1)
、
C(1,
-2)为此花坛的三个顶点,你能根据这三个点的坐标写出第四个顶点D的坐标吗?点D是唯一的吗?
解析:先建立直角坐标系,因为题中
只给定了三点坐标,要形成平行四边
形,最好通过画图来探索第四个点的位置,可以发现第四点位置不是唯一的。
x
y
0
.
A
B
.
.
C
.
D
.
D
.
D
(-3,2)
(1,-2)
(-3,-1)
(1,-5)
(-7,3)
(1,1)
4:如图是某个小岛的平面示意图,请你建立适当的平面直角坐标系,写出哨所1,哨所2,小广场,雷达,码头,营房的位置。
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
0
解析:
小广场居中
,那么以小
广场为原点
建立坐标系
最恰当。
所求坐标
依次是:
(0,3),
(-
4,0),
(0,0),
(4,0),
(-1,-3)
(1,-4)
学
习
目
标
1、认识平面直角坐标系,了解点与坐标的对应关系;
2、能在方格纸中建立适当的平面直角坐标系描述物体的位置,体会平面直角坐标系在解决实际问题中的作用;
3、能用坐标表示平移变换,通过研究平移与坐标关系,使学生看到平面直角坐标系是数与形之间的桥梁。
重、难点:会灵活运用平面直角坐标系的知识点解决问题
本章知识结构图
确定平面内点的位置
画两条数轴
①互相垂直
②有公共原点
建立平面直角坐标系
坐标(有序数对),(x,
y)
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示位置
用坐标表示平移
有序数对
一、有序数对的概念:
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对,记作(a
,
b).
理解有序数对时注意:
(1)不能随意交换两个数的位置。(3,5)和(5,3)表示不同的两个个位置。
(2)两个数组成的有序数对是个整体,不能分开。
5
可
明
个
万
女
4
中
我
的
一
学
3
爱
英
天
帅
活
2
球
里
是
生
大
1
小
孩
打
习
哥
A
B
C
D
E
1、如右图,方块中有25个汉字,用(C,3)表示“天”那么按下列要求排列会组成一句什么话,把它读出来。
(1)(A,5
)
(A,3)
(C,4
)
(E,5
)
(B,1)
(C,2)
(B,4)
(2)(B,4)
(C,2)
(D,4)
(C,5)
(A,1)
(D,3)
(E,1)
可
爱
的
女
孩
是
我
我
是
一
个
小
帅
哥
反馈练习:有序数对的应用
(3)确定小区中住户的位置必须有四个数据,分别为楼号a,单元号b,层数c和住户号d,即“a楼b单元c层d号。”
(4)区域定位法:绘出所在区域代号如B3,D5等。排球比赛队员场上的位置等。
生活中还有哪些确定位置的其他方法?
(1)如果全班同学站成一列做早操,现在教师想找某个同学,是否还需要用2个数据呢?
(2)多层电影院确定座位位置用两个数据够用吗?
必须有三个数据(a,b,c),其中a表示层数,b表示排号,c表示座号,即“a层b排c号”。
5
-2
-3
-4
-1
3
2
4
1
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
原点
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注
意:坐标轴上的点不属于任何象限。
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
(3,2)
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3,
2)
记作:A(3,2)
先横后纵呆括号,
中间逗号来隔开
(-4,1)
B
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y)和它对应。
这个有序实数对(x,y)就是这个点的坐标。
平面直角坐标系基础知识
1、平面直角坐标系是由有____的互相___的两条数轴组成的。水平的数轴称为____或____,习惯上取向___为正方向;竖直的数轴称为____或_____,取向___为正方向;两坐标轴的交点为平面直角系的____。
2、四个象限内点的坐标特征:第一象限:___;第二象限:____;第三象限:____;
第四象限:____
3、原点的坐标为_____,x轴上点的坐标特征:___,y轴上点的坐标特征:_____。
4、点P(x,y)到x轴的距离是______,到y轴的距离是______。
反馈练面直角坐标系的基础知识的运用
1、
已知坐标平面内点
P(a,a-b)在第四象限,那么点
Q(-a,b)
在
第____象限
2.如果点P(a+5,a?2)在y轴上,那么P点坐标为_____.
3.点A(?2,
-1)与x轴的距离是___;与y轴的距离是____.
4、点A在x轴上,距离原点4个单位长度,则A点的坐标是_____.
5、若点P在第二象限内,且到X轴和Y轴的距离分别是3和4,则点P的坐标为______.
(2)、如果两个点连线与x轴平行,那么这两个点的坐标有何特点?
如果两个点连线与y轴平行,那么这两个点的坐标有何特点?
0
1
1
x
y
A
B
C
D
E
F
G
H
(1)、每一个象限内的点的坐标在符号上有何特点?
研行(垂直)于坐标轴的直线上的点的坐标特征
知识要点:平行于x轴(垂直于Y轴)的直线上的点的____相同;平行于y轴(垂直于X轴)的直线上的点的_____相同。
反馈练习:
1、直线AB∥X轴,且点A(2,-3),若点B在坐标轴上,那么点B的坐标为_____
2、已知线段MN垂直于X轴,点M的坐标是(-1,3),若MN=4,则点N的坐标是_____.
研习三
角平分线上的点的坐标特征
知识要点:平面直角坐标系第一、三象限的角平分线上点的坐标特征_________,第二、四象限的角平分线上点的坐标特征________。
归纳:到坐标轴距离相等的点的坐标特征____
反馈练习:
1、
已知点P的坐标为(3a-2,a+6),且点P到两坐标轴距离相等,求a的值和P点坐标
研移和对称的点的坐标特征
知识要点:
1、点(x,y)向右或向左平移a个单位长度,可得到对应点_________或_________;点(x,y)向上或向下平移b个单位长度,可得到对应点_________或_________。
2、点M(a,b)关于x轴的对称点坐标是______,关于y轴的对称点是______,关于原点的对称点是_______
反馈练习
1、一只青蛙从点A(-1,0)处先向右跳2个单位长度,在向下跳2个单位长度到达B处,则B的坐标是____
2、线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标是______
3、点A
(4,-1)与点B关于X轴对称,则点B坐标是_____,AB=____
4、点O(x+y,2x+y)与点P(5,-10)关于Y轴对称,则点(x,y)坐标为______
研习五
两点间距离和面积的计算
知识要点:
1、在平面直角坐标系中,平行于坐标轴的直线上两点O(x,y)与P(a,b)
,OP=
_____
2、平面直角坐标系中,面积的计算,可以直接用公式计算,也可以借助三角形、长方形等特殊的图形和差来计算,计算时一定要看清楚图形的各边的长度
练习:1.点A(-5,0)点B(3,0),三角形ABC的面积是12,点C在Y轴上,求C点坐标;
变式:上题中C点若在X轴上或在X=3直线上,C点坐标怎样求?
1.已知:A(0,1),B(1,0),C(3,2).
(1)求△ABC的面积;
(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,直接写出点P坐标.
2、如右图
(1)将三角形ABC向左平移3格再向下平移2格后得到的三角形A1B1C1的坐标为___,三角形A1B1C1的面积是_____;
A
B
C
y
x
O
(2)在平面直角坐标系内是否存在一点D能使四边形ABCD构成平行四边形,若有请写出点D的坐标?
3:要修建一个平行四边形的花坛,
A(-3,2)、B
(-3
,-1)
、
C(1,
-2)为此花坛的三个顶点,你能根据这三个点的坐标写出第四个顶点D的坐标吗?点D是唯一的吗?
解析:先建立直角坐标系,因为题中
只给定了三点坐标,要形成平行四边
形,最好通过画图来探索第四个点的位置,可以发现第四点位置不是唯一的。
x
y
0
.
A
B
.
.
C
.
D
.
D
.
D
(-3,2)
(1,-2)
(-3,-1)
(1,-5)
(-7,3)
(1,1)
4:如图是某个小岛的平面示意图,请你建立适当的平面直角坐标系,写出哨所1,哨所2,小广场,雷达,码头,营房的位置。
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
0
解析:
小广场居中
,那么以小
广场为原点
建立坐标系
最恰当。
所求坐标
依次是:
(0,3),
(-
4,0),
(0,0),
(4,0),
(-1,-3)
(1,-4)
