人教版七年级下册数学 6.1平方根(共36张ppt)
文档属性
| 名称 | 人教版七年级下册数学 6.1平方根(共36张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览











文档简介
6.1平方根
知设情境,引入新课
请同学们阅读本章的引言.
你从引言中发现了哪些与数有关的概念?
本章将要学习的主要内容以及大致的研究思路是什么?
问题1:
请说一说,你是怎样算出来的?
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
问题2:
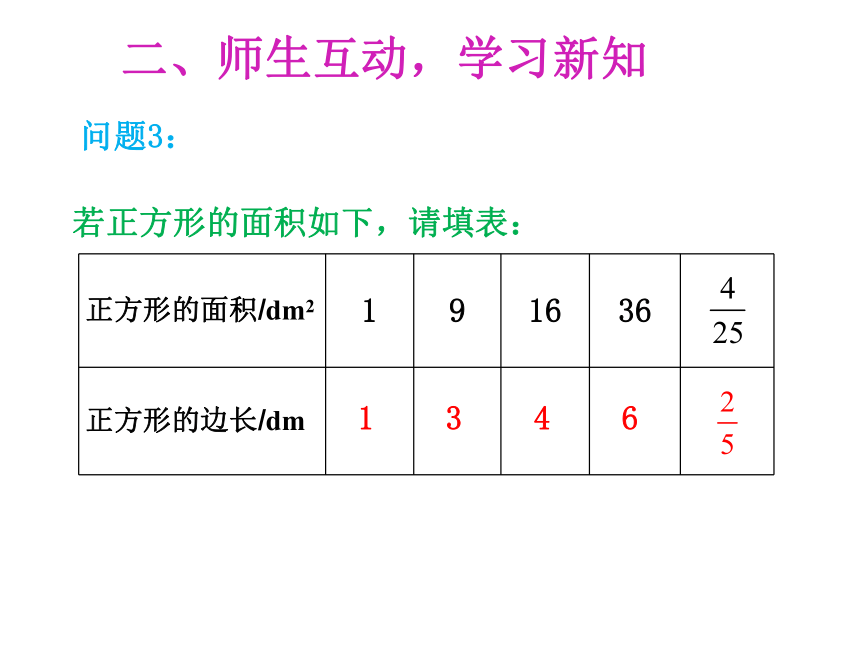
二、师生互动,学习新知
若正方形的面积如下,请填表:
正方形的面积/dm2
1
9
16
36
正方形的边长/dm
问题3:
1
3
4
6
二、师生互动,学习新知
上面的问题,可以归纳为“已知一个正数的平方,
求这个正数”的问题.
实际上是乘方运算中,已知一个数的指数和它的
幂,求这个数.
二、师生互动,学习新知
问题4:
你能指出问题2与问题3的共同特点吗?
定义:
一般地,如果一个正数 x 的平方等于 a,即 x2=a,
那么这个正数 x 叫做a的算术平方根.a的算术平方根
记为 ,读作“根号a”,a 叫做被开方数.
规定:0的算术平方根是0 .
问题5:0的算术平方根是多少?
怎么表示?
根号
a的算术平方根
二、师生互动,学习新知
被开方数
根据以上学习,你认为对于算术平方根中被开方数可以是哪些数?
为什么负数没有算术平方根呢?
二、师生互动,学习新知
0或正数(即“非负数”)
因为没有那个数的平方等于负数.
根据算术平方根的定义,试回答:9的算术平方根是多少?0的算术平方根是多少?-4呢
由此可见,若 有意义,那么被开方数 一定是一个 数.
非 负
归 纳
(1)一个正数 的算术平方根是
(3)负数没有算术平方根
(2)0 的算术平方根是0,即
要注意
探究
1、a可以取任何数吗?
2、 是什么数?
(1)被开方数a是非负数,即
(2) 是非负数,即
算术平方根具有双重非负性
(1)-5是-25的算术平方根;
(2)6是62的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)一个正方形的边长就是这个正方形的面积
的算术平方根.
判断正误:
√
√
√
二、师生互动,学习新知
×
×
例1 求下列各数的算术平方根:
⑴ ; ⑵ ; ⑶ .
解:⑴因为102=100,
所以100的算术平方根是10.
即 .
三、举例示范,应用新知
例1 求下列各数的算术平方根:
⑴ ; ⑵ ; ⑶ .
解:(2)因为 ,
所以 的算术平方根是 .
即 .
三、举例示范,应用新知
例1 求下列各数的算术平方根:
⑴ ; ⑵ ; ⑶ .
解:(3)因为0.012=0.0001,
所以0.0001的算术平方根是0.01.
即 .
三、举例示范,应用新知
问题6:(1)被开方数的大小与对应的算术平方根
的大小之间有什么关系呢?
结论:被开方数越大,对应的算术平方根也越大.
问题6:(2)请你再举一些具体的例子加以说明.
三、举例示范,应用新知
例2 求下列各式的值.
⑴ ; ⑵ ; ⑶ .
解:(1)因为 62=36,
所以36的算术平方根是6.
即 =6.
三、举例示范,应用新知
例2 求下列各式的值.
⑴ ; ⑵ ; ⑶ .
解:(2)因为42的算术平方根是4,
所以 =4.
三、举例示范,应用新知
例2 求下列各式的值.
⑴ ; ⑵ ; ⑶ .
解:(3)因为 ,而 的算术平方根是 ,
所以 .
三、举例示范,应用新知
4.如果一个正方形的面积是1.21平方米,那么
它的边长为 米.
2.若 ,则 .
(1) ;(2) ;(3) .
3.求下列各式的值:
1. 下列各式没有意义的是( )
A. B. C. D.
B
49
1.1
13
0.2
四、及时练习,巩固新知
5.求下列各数的算术平方根:
⑴0.0025; ⑵81; ⑶32.
6.求下列各式的值:
⑴ ; ⑵ ; ⑶ .
7.求 的算术平方根.
四、及时练习,巩固新知
3.若 的算术平方根是4,则 .
2.16的算术平方根是 ; 的算术平方根是 .
1. 算术平方根是它本身的数是 .
拓展提高
0和1
4
2
16
4.如果 有意义,那么 的取值范围是 .
新人教版七年级数学下册第六章
实 数
6.1平方根(2)
复习与回顾
2. 判断下列各数有没有算术平方根,如果有,请求出它们的算术平方根。
100;1; 0; -0.0025; (-3)2 ; -25;2
1. 什么叫做算术平方根?
一般地,如果一个正数x的平方等于a,
即 ,那么这个正数x 叫做a的算术平方根。
a的算术平方根记为:
读作:“根号a”,
a叫做被开方数。
负数没有算术平方根.
你知道 有多大吗?
二、问题探究,学习新知
(1)能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形?
探究:
(2)拼成的这个面积为2dm2的大正方形的边长应该是多少呢?
?
(3)小正方形的对角线的长是多少呢?
因为 , ,而1< 2<4,所以 .
(1) 在哪两个整数之间呢?
(2)你能不能得到 的更精确的范围?
根据是什么?
因为 , ,而 ,
所以 .
因为 , ,
而 ,所以 .
因为 , ,
而 ,所以 .
……
探究:
有多大呢?
你以前见过这种数吗?
探究:
有多大呢?
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
它是一个无限不循环小数,许多正有理数的算术平方根(例如 , , 等)都是无限不循环小数.
1.估计 的整数部分是____.
2.估计 的大小范围是( ).
A.7.5~8.0 B.8.0~8.5
C.8.5~9.0 D.9.0~9.5
练习
2
C
例1 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
(2)依次按键 2
显示:1.414213562.
∴ .
解:(1)依次按键 3136
显示:56.
∴ .
这是准确数吗?
例题分析
练习
用计算器求下列各式的值:
(1) ;
(2) ;
(3) (精确到0.001).
(1)你会表示 , 吗?
(2)用计算器求 , .(结果用科学记数法表示)
1.解决章引言中提出的问题
你知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围吗?这时它的速度要大于第一宇宙速度 (单位: )而小于第二宇宙速度 (单位: ). , 的大小满足 , ,其中 ,R是地球半径, .怎样求 , 呢?
问题解决
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
…
…
…
…
2.探究规律
被开方数每扩大100倍,其算术平方根就扩大10倍.
被开方数的小数点向右或向左移动2位,它的算术平方根的小数点就相应地向右或向左移动1位.
0.25
0.791
2.5
25
250
7.91
79.1
问题解决
(1)你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
(2)你能否根据 的值说出 是多少?
应用规律
不能
例2 小丽想用一块面积为400cm2的长方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
3.估计大小的实际应用
问题解决
(1)你能将这个问题转化为数学问题吗?
(3)长方形的长和宽与正方形的边长之间的大小关系是什么?
(2)如何求出长方形的长和宽?
例2 小丽想用一块面积为400cm2为的长方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.
(4)小丽能用这块纸片裁出符合要求的纸片吗?
问题解决
解:设长方形纸片的长为3x cm,宽为2x cm.
根据边长与面积的关系得
3x ? 2x=300 ,
6x2=300 ,
x2=50,
,
故长方形纸片的长为 ,宽为 .
因为50>49,得 >7,所以 >3×7=21,比原正方形的边长更长,这是不可能的.所以,小丽不能用这块纸片裁出符合要求的纸片.
问题解决
巩固练习
1、 的整数部分是 ;
2、一个正方形的面积是15,则估计它的边长的大小
在( )
A、2与3之间 B、3与4之间
C、4与5之间 D、5与6之间
3、若 ,则:
, 。
1、无限不循环小数是_________________
______________ 的小数.
2、当被开方数的小数点向右移动2位时,算术平方根的小数点只向_____移动____位;
当被开方数的小数点向左移动2位时,算术平方根的小数点只向_____移动_____位.
3、学习反思:________________________
_____________________________________
____________________________________.
右
1
左
1
且小数部分不循环
是指小数位数无限,
归纳小结
知设情境,引入新课
请同学们阅读本章的引言.
你从引言中发现了哪些与数有关的概念?
本章将要学习的主要内容以及大致的研究思路是什么?
问题1:
请说一说,你是怎样算出来的?
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
问题2:
二、师生互动,学习新知
若正方形的面积如下,请填表:
正方形的面积/dm2
1
9
16
36
正方形的边长/dm
问题3:
1
3
4
6
二、师生互动,学习新知
上面的问题,可以归纳为“已知一个正数的平方,
求这个正数”的问题.
实际上是乘方运算中,已知一个数的指数和它的
幂,求这个数.
二、师生互动,学习新知
问题4:
你能指出问题2与问题3的共同特点吗?
定义:
一般地,如果一个正数 x 的平方等于 a,即 x2=a,
那么这个正数 x 叫做a的算术平方根.a的算术平方根
记为 ,读作“根号a”,a 叫做被开方数.
规定:0的算术平方根是0 .
问题5:0的算术平方根是多少?
怎么表示?
根号
a的算术平方根
二、师生互动,学习新知
被开方数
根据以上学习,你认为对于算术平方根中被开方数可以是哪些数?
为什么负数没有算术平方根呢?
二、师生互动,学习新知
0或正数(即“非负数”)
因为没有那个数的平方等于负数.
根据算术平方根的定义,试回答:9的算术平方根是多少?0的算术平方根是多少?-4呢
由此可见,若 有意义,那么被开方数 一定是一个 数.
非 负
归 纳
(1)一个正数 的算术平方根是
(3)负数没有算术平方根
(2)0 的算术平方根是0,即
要注意
探究
1、a可以取任何数吗?
2、 是什么数?
(1)被开方数a是非负数,即
(2) 是非负数,即
算术平方根具有双重非负性
(1)-5是-25的算术平方根;
(2)6是62的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)一个正方形的边长就是这个正方形的面积
的算术平方根.
判断正误:
√
√
√
二、师生互动,学习新知
×
×
例1 求下列各数的算术平方根:
⑴ ; ⑵ ; ⑶ .
解:⑴因为102=100,
所以100的算术平方根是10.
即 .
三、举例示范,应用新知
例1 求下列各数的算术平方根:
⑴ ; ⑵ ; ⑶ .
解:(2)因为 ,
所以 的算术平方根是 .
即 .
三、举例示范,应用新知
例1 求下列各数的算术平方根:
⑴ ; ⑵ ; ⑶ .
解:(3)因为0.012=0.0001,
所以0.0001的算术平方根是0.01.
即 .
三、举例示范,应用新知
问题6:(1)被开方数的大小与对应的算术平方根
的大小之间有什么关系呢?
结论:被开方数越大,对应的算术平方根也越大.
问题6:(2)请你再举一些具体的例子加以说明.
三、举例示范,应用新知
例2 求下列各式的值.
⑴ ; ⑵ ; ⑶ .
解:(1)因为 62=36,
所以36的算术平方根是6.
即 =6.
三、举例示范,应用新知
例2 求下列各式的值.
⑴ ; ⑵ ; ⑶ .
解:(2)因为42的算术平方根是4,
所以 =4.
三、举例示范,应用新知
例2 求下列各式的值.
⑴ ; ⑵ ; ⑶ .
解:(3)因为 ,而 的算术平方根是 ,
所以 .
三、举例示范,应用新知
4.如果一个正方形的面积是1.21平方米,那么
它的边长为 米.
2.若 ,则 .
(1) ;(2) ;(3) .
3.求下列各式的值:
1. 下列各式没有意义的是( )
A. B. C. D.
B
49
1.1
13
0.2
四、及时练习,巩固新知
5.求下列各数的算术平方根:
⑴0.0025; ⑵81; ⑶32.
6.求下列各式的值:
⑴ ; ⑵ ; ⑶ .
7.求 的算术平方根.
四、及时练习,巩固新知
3.若 的算术平方根是4,则 .
2.16的算术平方根是 ; 的算术平方根是 .
1. 算术平方根是它本身的数是 .
拓展提高
0和1
4
2
16
4.如果 有意义,那么 的取值范围是 .
新人教版七年级数学下册第六章
实 数
6.1平方根(2)
复习与回顾
2. 判断下列各数有没有算术平方根,如果有,请求出它们的算术平方根。
100;1; 0; -0.0025; (-3)2 ; -25;2
1. 什么叫做算术平方根?
一般地,如果一个正数x的平方等于a,
即 ,那么这个正数x 叫做a的算术平方根。
a的算术平方根记为:
读作:“根号a”,
a叫做被开方数。
负数没有算术平方根.
你知道 有多大吗?
二、问题探究,学习新知
(1)能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形?
探究:
(2)拼成的这个面积为2dm2的大正方形的边长应该是多少呢?
?
(3)小正方形的对角线的长是多少呢?
因为 , ,而1< 2<4,所以 .
(1) 在哪两个整数之间呢?
(2)你能不能得到 的更精确的范围?
根据是什么?
因为 , ,而 ,
所以 .
因为 , ,
而 ,所以 .
因为 , ,
而 ,所以 .
……
探究:
有多大呢?
你以前见过这种数吗?
探究:
有多大呢?
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
它是一个无限不循环小数,许多正有理数的算术平方根(例如 , , 等)都是无限不循环小数.
1.估计 的整数部分是____.
2.估计 的大小范围是( ).
A.7.5~8.0 B.8.0~8.5
C.8.5~9.0 D.9.0~9.5
练习
2
C
例1 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
(2)依次按键 2
显示:1.414213562.
∴ .
解:(1)依次按键 3136
显示:56.
∴ .
这是准确数吗?
例题分析
练习
用计算器求下列各式的值:
(1) ;
(2) ;
(3) (精确到0.001).
(1)你会表示 , 吗?
(2)用计算器求 , .(结果用科学记数法表示)
1.解决章引言中提出的问题
你知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围吗?这时它的速度要大于第一宇宙速度 (单位: )而小于第二宇宙速度 (单位: ). , 的大小满足 , ,其中 ,R是地球半径, .怎样求 , 呢?
问题解决
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
…
…
…
…
2.探究规律
被开方数每扩大100倍,其算术平方根就扩大10倍.
被开方数的小数点向右或向左移动2位,它的算术平方根的小数点就相应地向右或向左移动1位.
0.25
0.791
2.5
25
250
7.91
79.1
问题解决
(1)你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
(2)你能否根据 的值说出 是多少?
应用规律
不能
例2 小丽想用一块面积为400cm2的长方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
3.估计大小的实际应用
问题解决
(1)你能将这个问题转化为数学问题吗?
(3)长方形的长和宽与正方形的边长之间的大小关系是什么?
(2)如何求出长方形的长和宽?
例2 小丽想用一块面积为400cm2为的长方形纸片,沿着边的方向剪出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2.
(4)小丽能用这块纸片裁出符合要求的纸片吗?
问题解决
解:设长方形纸片的长为3x cm,宽为2x cm.
根据边长与面积的关系得
3x ? 2x=300 ,
6x2=300 ,
x2=50,
,
故长方形纸片的长为 ,宽为 .
因为50>49,得 >7,所以 >3×7=21,比原正方形的边长更长,这是不可能的.所以,小丽不能用这块纸片裁出符合要求的纸片.
问题解决
巩固练习
1、 的整数部分是 ;
2、一个正方形的面积是15,则估计它的边长的大小
在( )
A、2与3之间 B、3与4之间
C、4与5之间 D、5与6之间
3、若 ,则:
, 。
1、无限不循环小数是_________________
______________ 的小数.
2、当被开方数的小数点向右移动2位时,算术平方根的小数点只向_____移动____位;
当被开方数的小数点向左移动2位时,算术平方根的小数点只向_____移动_____位.
3、学习反思:________________________
_____________________________________
____________________________________.
右
1
左
1
且小数部分不循环
是指小数位数无限,
归纳小结
