人教版七年级下数学9.1.2不等式及其基本性质(共32张PPT)
文档属性
| 名称 | 人教版七年级下数学9.1.2不等式及其基本性质(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 22:04:50 | ||
图片预览










文档简介
班级----我的家---全靠
我
他
你
焦陂职高丁勇
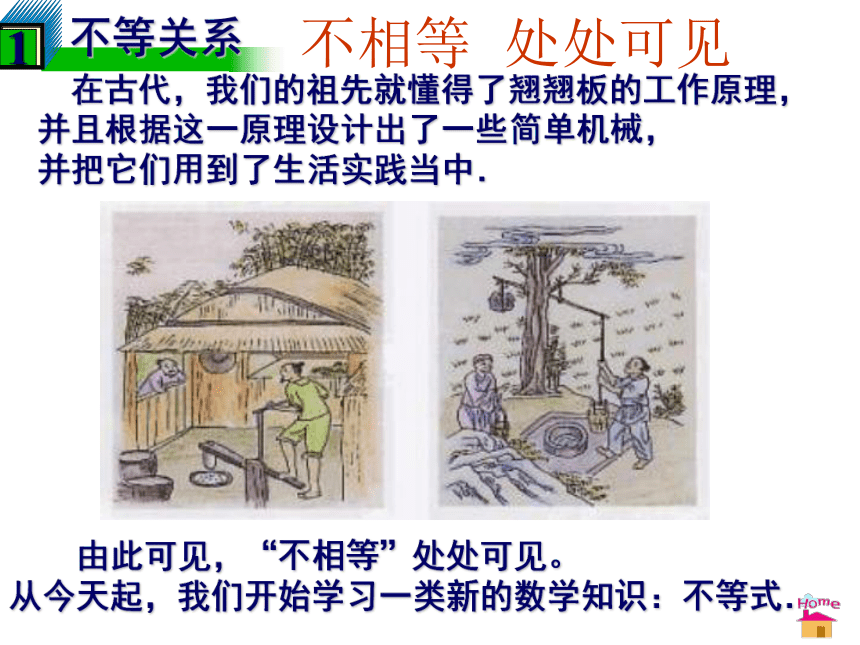
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
从今天起,我们开始学习一类新的数学知识:不等式.
不相等 处处可见
1
不等关系
问题1:雷电的温度大约是28000℃,比太阳表面温度的4.5倍还要高。设太阳表面温度为t℃,那么t应该满足怎样的关系式?
问题2:一种药品每片为0.25g,说明书上写着:“每日用量0.75~2.25g,分3次服用”。设某人一次服用 片,那么 应满足怎样的关系?
问题3:用适当的符号表示下列关系:
(1) 与3的和不大于-6;
(2) 的5倍与1的差小于 的3倍;
(3)a与b的差是负数。
4t<28000
0.75≤0.75x≤2.25
2x+3≤6
a-b<0
5x-1<3x
不等式的定义
用不等号(>、≥、<、≤或≠)表示不等关系的式子叫做不等式
注:不大于,即小于或等于,用“≤”表示;
不小于,即大于或等于,用“≥”表示。
判断下列式子是不是不等式:
(1)-3<0; (2)4x+3y>0
(3)x=3;(4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
2
不等式的性质
等式具有那些性质?
不等式是否具有这些的性质?
由a+2=b+2, 你能得到a=b吗?
由0.5a=0.5b, 你能得到a=b吗?
由 -2a= -2b, 你能得到a=b吗?
由a-2=b-2, 你能得到a=b吗?
由a=b,你能得到b=a吗?
由a=b,b=c,你能得到a=c吗?
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
等式基本性质3(对称性)
如果a等式基本性质4(传递性)
如果a=b,b=c那么a=c
不等式是否具有类似的性质呢?
如果 7 > 3
那么 7+5 ____ 3+ 5 , 7 -5____3-5
你能总结一下规律吗?
>
>
如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4
<
<
+ C
-C
(或________)
如果_____,
那么_______
如果a>b,
那么a±c>b±c
b>a
b+c>a+c
b-c>a-c
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
如果____,那么_________.
不等号的方向不变。
a>b
a±c>b±c
_________________
7÷5 ____ 3÷ 5 ,
7 ÷ (-5)____3÷ (-5)
不等式还有什么类似的性质呢?
已知 7 > 3
那么 7×5 ____ 3× 5 ,
7 ×(-5)____3×(-5),
你能再总结一下规律吗?
>
>
已知-1< 3,
那么-1×2____3×2,
-1×(- 4)____3×( - 4),
-1÷2____3÷2,
-1÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
×3
÷3
(或 )
如果_________,
那么_______
a>b且c>0
ac>bc
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac思考:不等式具有对称性和传递性吗?
已知x>5,那么5由8不等式的对称性:
如果a>b,那么b不等式的同向传递性:
如果a>b,b>c,那么a>c
今天学的是不等式的五个基本性质:
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或同一整式),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式的对称性:
如果a>b,那么b不等式传递性:
如果a>b,b>c,那么a>c
不等式基本性质3:
如果a>b,c<0 那么ac例1:设a>b,用“<”或“>”填空并口答是根据哪一条不等式基本性质。
(1) a - 3____b - 3;
(2)a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6) (m2+1) a ____ (m2+1)b (m为常数)
>
>
>
>
>
<
例2:判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
针对练习
针对练习
(1)如果x-5>4,那么两边都 可得到x>9
(2)如果在-7<8的两边都加上9可得到
(3)如果在5>-2的两边都加上a+2可得到
(4)如果在-3>-4的两边都乘以7可得到
(5)如果在8>0的两边都乘以8可得到
(6)如果在 的两边都乘以14
可得到
X
7
>2+
X
2
加上5
2 < 17
a+7 > a
-21>-28
64 > 0
2x>28+7x
1、若m>n,判断下列不等式是否正确:
(1)m-7(2)3m<3n ( )
(3)-5m>-5n ( )
(4) ( )
(5) m+5≥n+5 ( )
针对练习
填空:
(1) ∵ 2a < 3a , ∴a是____数
(3) ∵ ax < a 且 x > 1 ,
∴a是____数
(2) ∵ , ∴a是____数
正
正
负
1、已知 a < - 1 ,则下列不等式中错误的是( )
A、4a < - 4 B、- 4a < 4 C、a + 2 < 1 D、2 – a > 3
2、已知x < y,下列哪些不等式成立?
(1) x – 3 < y – 3 (2)- 5 x < - 5 y
(3) - 3 x +2 < - 3 y + 2 (4)- 3 x + 2 > - 3y + 2
3、已知a>b,若a<0,则a2 ab;若a>0,则a2 ab.
4、下列各式分别在什么条件下成立?
(1) a > - a (2) a2 > a
B
<
>
今天学的是不等式的五个基本性质:
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式的对称性:
如果a>b,那么b不等式传递性:
如果a>b,b>c,那么a>c
不等式基本性质3:
如果a>b,c<0 那么ac小结:
①在利用不等式的基本性质进行变形时,当不等式的两边都乘以(或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式基本性质2还是基本性质3,也就是不等号是否要改变方向的问题;
②运用不等式基本性质3时,要变两个号,一个性质符号,另一个是不等号.
作业:习题7.1第2、3题
www.1230.org 初中数学资源网
我
他
你
焦陂职高丁勇
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
从今天起,我们开始学习一类新的数学知识:不等式.
不相等 处处可见
1
不等关系
问题1:雷电的温度大约是28000℃,比太阳表面温度的4.5倍还要高。设太阳表面温度为t℃,那么t应该满足怎样的关系式?
问题2:一种药品每片为0.25g,说明书上写着:“每日用量0.75~2.25g,分3次服用”。设某人一次服用 片,那么 应满足怎样的关系?
问题3:用适当的符号表示下列关系:
(1) 与3的和不大于-6;
(2) 的5倍与1的差小于 的3倍;
(3)a与b的差是负数。
4t<28000
0.75≤0.75x≤2.25
2x+3≤6
a-b<0
5x-1<3x
不等式的定义
用不等号(>、≥、<、≤或≠)表示不等关系的式子叫做不等式
注:不大于,即小于或等于,用“≤”表示;
不小于,即大于或等于,用“≥”表示。
判断下列式子是不是不等式:
(1)-3<0; (2)4x+3y>0
(3)x=3;(4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
2
不等式的性质
等式具有那些性质?
不等式是否具有这些的性质?
由a+2=b+2, 你能得到a=b吗?
由0.5a=0.5b, 你能得到a=b吗?
由 -2a= -2b, 你能得到a=b吗?
由a-2=b-2, 你能得到a=b吗?
由a=b,你能得到b=a吗?
由a=b,b=c,你能得到a=c吗?
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
等式基本性质3(对称性)
如果a
如果a=b,b=c那么a=c
不等式是否具有类似的性质呢?
如果 7 > 3
那么 7+5 ____ 3+ 5 , 7 -5____3-5
你能总结一下规律吗?
>
>
如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4
<
<
+ C
-C
(或________)
如果_____,
那么_______
如果a>b,
那么a±c>b±c
b>a
b+c>a+c
b-c>a-c
不等式基本性质1:不等式的两边都加上(或减去)同一个整式,
如果____,那么_________.
不等号的方向不变。
a>b
a±c>b±c
_________________
7÷5 ____ 3÷ 5 ,
7 ÷ (-5)____3÷ (-5)
不等式还有什么类似的性质呢?
已知 7 > 3
那么 7×5 ____ 3× 5 ,
7 ×(-5)____3×(-5),
你能再总结一下规律吗?
>
>
已知-1< 3,
那么-1×2____3×2,
-1×(- 4)____3×( - 4),
-1÷2____3÷2,
-1÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
×3
÷3
(或 )
如果_________,
那么_______
a>b且c>0
ac>bc
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac
已知x>5,那么5
如果a>b,那么b不等式的同向传递性:
如果a>b,b>c,那么a>c
今天学的是不等式的五个基本性质:
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或同一整式),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式的对称性:
如果a>b,那么b不等式传递性:
如果a>b,b>c,那么a>c
不等式基本性质3:
如果a>b,c<0 那么ac
(1) a - 3____b - 3;
(2)a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6) (m2+1) a ____ (m2+1)b (m为常数)
>
>
>
>
>
<
例2:判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
针对练习
针对练习
(1)如果x-5>4,那么两边都 可得到x>9
(2)如果在-7<8的两边都加上9可得到
(3)如果在5>-2的两边都加上a+2可得到
(4)如果在-3>-4的两边都乘以7可得到
(5)如果在8>0的两边都乘以8可得到
(6)如果在 的两边都乘以14
可得到
X
7
>2+
X
2
加上5
2 < 17
a+7 > a
-21>-28
64 > 0
2x>28+7x
1、若m>n,判断下列不等式是否正确:
(1)m-7
(3)-5m>-5n ( )
(4) ( )
(5) m+5≥n+5 ( )
针对练习
填空:
(1) ∵ 2a < 3a , ∴a是____数
(3) ∵ ax < a 且 x > 1 ,
∴a是____数
(2) ∵ , ∴a是____数
正
正
负
1、已知 a < - 1 ,则下列不等式中错误的是( )
A、4a < - 4 B、- 4a < 4 C、a + 2 < 1 D、2 – a > 3
2、已知x < y,下列哪些不等式成立?
(1) x – 3 < y – 3 (2)- 5 x < - 5 y
(3) - 3 x +2 < - 3 y + 2 (4)- 3 x + 2 > - 3y + 2
3、已知a>b,若a<0,则a2 ab;若a>0,则a2 ab.
4、下列各式分别在什么条件下成立?
(1) a > - a (2) a2 > a
B
<
>
今天学的是不等式的五个基本性质:
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式的对称性:
如果a>b,那么b不等式传递性:
如果a>b,b>c,那么a>c
不等式基本性质3:
如果a>b,c<0 那么ac
①在利用不等式的基本性质进行变形时,当不等式的两边都乘以(或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式基本性质2还是基本性质3,也就是不等号是否要改变方向的问题;
②运用不等式基本性质3时,要变两个号,一个性质符号,另一个是不等号.
作业:习题7.1第2、3题
www.1230.org 初中数学资源网
