人教版七年级下数学9.3一元一次不等式组解法课件(共19张PPT)
文档属性
| 名称 | 人教版七年级下数学9.3一元一次不等式组解法课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 22:12:30 | ||
图片预览



文档简介
欢迎各位领导老师的莅临指导!
退出
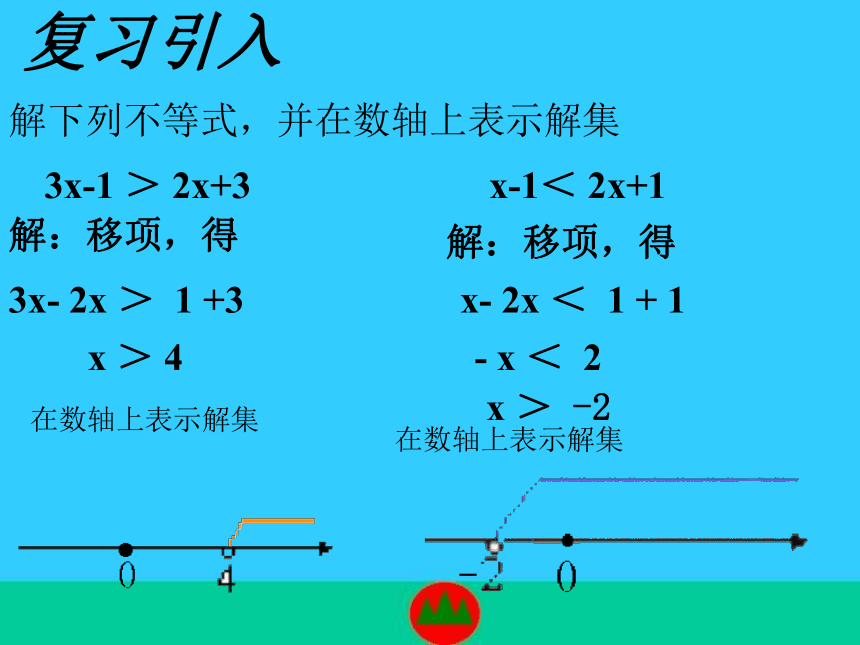
3x-1 > 2x+3
x-1< 2x+1
复习引入
解下列不等式,并在数轴上表示解集
解:移项,得
x > 4
3x- 2x > 1 +3
解:移项,得
x- 2x < 1 + 1
- x < 2
x > -2
在数轴上表示解集
在数轴上表示解集
3x-1 > 2x+3
x-1< 2x+1 ②
①
几个一元一次不等式合在一起就构成
一元一次不等式组
y -1 ≥ 0
一.判断题:(1)
x +2 >0
是一元一次不等式组
( )
(2)
x+3 ≤ 6
x < 1
是一元一次不等式组 ( )
错
对
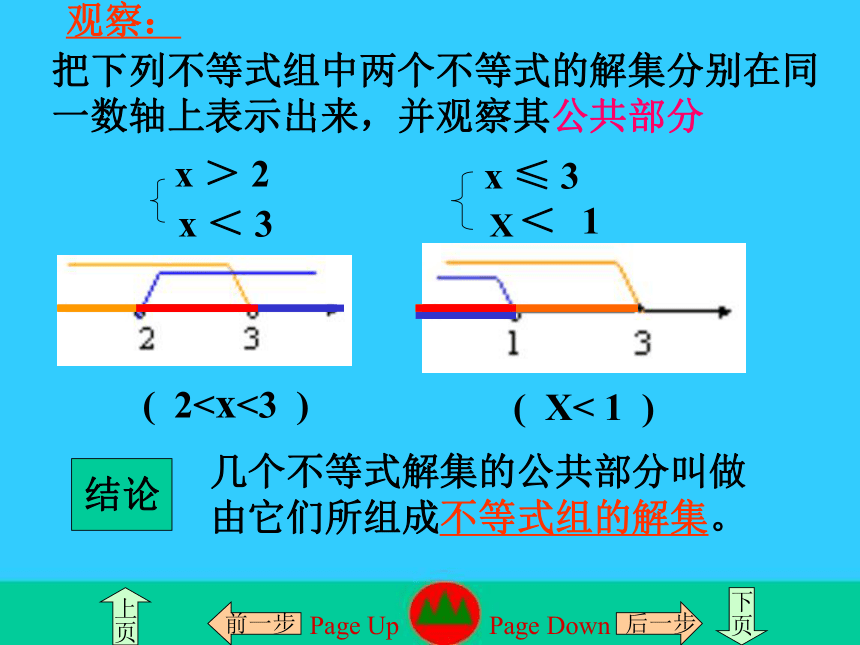
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分
观察:
结论
几个不等式解集的公共部分叫做由它们所组成不等式组的解集。
x > 2
x < 3
x ≤ 3
X
<
1
前一步
Page Up
Page Down
后一步
上页
下页
( 2( X< 1 )
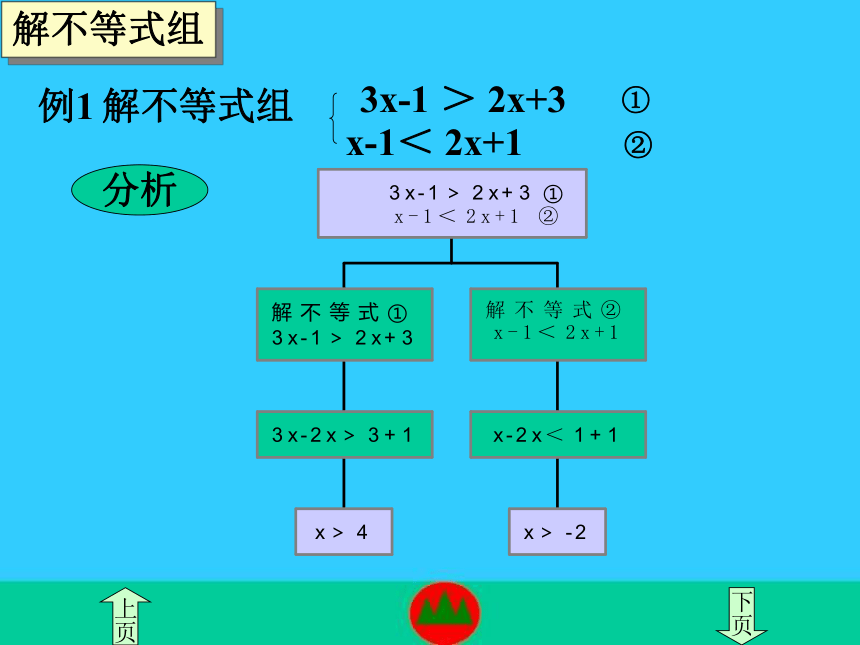
例1 解不等式组
3x-1 > 2x+3
x-1< 2x+1 ②
①
解不等式组
分析
上页
下页
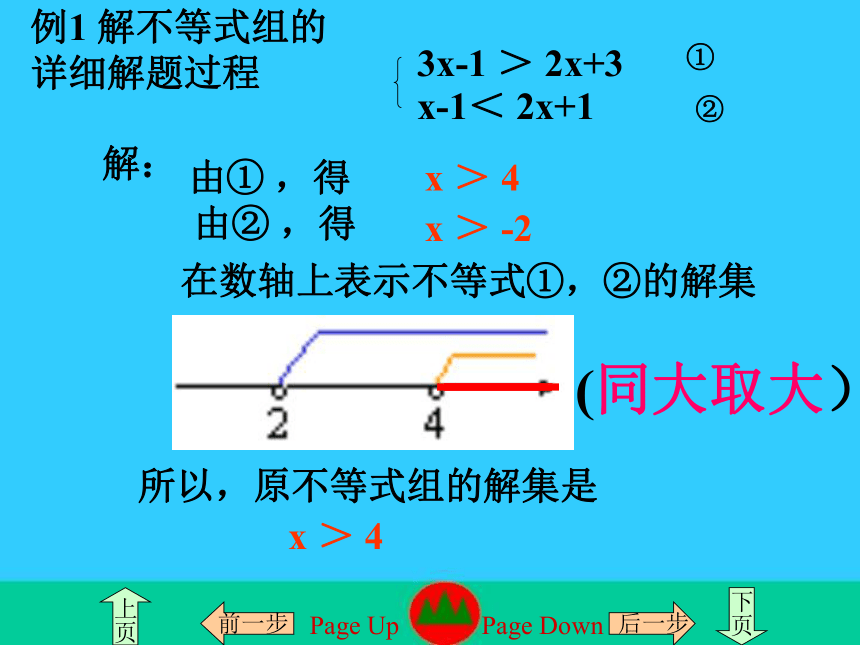
例1 解不等式组的 详细解题过程
①
3x-1 > 2x+3
x-1< 2x+1 ②
解:
由① ,得
由② ,得
x > 4
x > -2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
x > 4
前一步
后一步
Page Up
Page Down
上页
下页
(同大取大)
例2 解不等式组
x+3 ≤ 6
①
解:
解不等式① ,得
解不等式② ,得
x ≤ 3
x <1
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
②
x <1
2x+7
<
前一步
后一步
Page Up
Page Down
上页
下页
x+8
(同小取小)
例3 解不等式组
2x+3 <5
3x-2 >4 ②
①
解:
解不等式① ,得
解不等式② ,得
x < 1
x > 2
在数轴上表示不等式①,②的解集
所以,原不等式组无解
(观察:数轴上有无公共部分)
前一步
后一步
Page Up
Page Down
上页
下页
(相背取空)
例 4 解不等式组
5x -2> 3x+3
①
解:
解不等式① ,得
解不等式② ,得
x > 2.5
x ≤ 4
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
2.5 < x ≤ 4
②
x-1
≤ 7 - x
退出
主页
前一步
后一步
Page Up
Page Down
(相对取中)
1.你能总结一下解一元一次不等式组的解题步骤吗?
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分,
也就是求出了这个不等式组的解集。
上页
下页
议一议
反馈测评
一选择题 1.选择下列不等式组的解集
上页
下页
①
x ≥ -1
x≥ 2
x≥ 2
x ≥ -1
-1≤ x≤ 2
无解
A
C
D
B
②
x< -1
x< 2
x< 2
x< -1
-1< x< 2
无解
B
D
C
A
A
无解
③
x ≥ -1
x ≥ -1
x< 2
x< 2
-1≤ x< 2
B
D
A
C
C
无解
x< -1
x< -1
④
x≥ 2
x≥ 2
-1< x≥ 2
C
B
A
D
D
B
2.不等式组
反馈测评
x +2 >0
x -1 ≥ 0
的解集在数轴上表示正确的是
3.下列不等式中,解集为x< - 4的是
x +4> 0
x +4 >0
x -5 < 0
x -5 < 0
x -5 >0
x +4 < 0
上页
下页
A
B
C
C
D
A
B
C
B
达标测评
二 . 解不等式组
2 (x+2) < x+5
3 (x-2)+8 >2x
①
②
解:
解不等式① ,得
解不等式② ,得
x < 1
x >-2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
- 2 < x<1
退出
主页
前一步
后一步
Page Up
Page Down
上页
下页
结束
小 结
(1)本节课主要学习了什么?
(2)你有什么体会?
解:设另找的木棒长为xcm,根据题意,得
10+3>x ①
10-3 有两木根棒a和b, 其中a长10cm, b长3cm,请找第三根木棒,使之与a,b构成三角形
探索题
7 < x <13
解不等式① ,得
x <13
解不等式② ,得
x >7
所以,原不等式组的解集是
答:第三根木棒长为
7 cm< x <13cm
一课一测(五分钟)
一.判断题:(1)
x +2 >0
y -1 ≥ 0
不是一元一次不等式组
( )
(2)
x > 3
x ≤ 5
原不等式组的解集是
3 < x < 5
( )
二.填空题:(1)满足不等式
-2 < x < 3的非零整数是______
(2)若不等式组
x>a x<b
无解,则a与b的大小关系是______
作业布置:1)课本147页复习 巩固2 2)课本148页4, 7,8
谢谢大家,欢迎提出宝贵意见!
再见!!
退出
3x-1 > 2x+3
x-1< 2x+1
复习引入
解下列不等式,并在数轴上表示解集
解:移项,得
x > 4
3x- 2x > 1 +3
解:移项,得
x- 2x < 1 + 1
- x < 2
x > -2
在数轴上表示解集
在数轴上表示解集
3x-1 > 2x+3
x-1< 2x+1 ②
①
几个一元一次不等式合在一起就构成
一元一次不等式组
y -1 ≥ 0
一.判断题:(1)
x +2 >0
是一元一次不等式组
( )
(2)
x+3 ≤ 6
x < 1
是一元一次不等式组 ( )
错
对
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分
观察:
结论
几个不等式解集的公共部分叫做由它们所组成不等式组的解集。
x > 2
x < 3
x ≤ 3
X
<
1
前一步
Page Up
Page Down
后一步
上页
下页
( 2
例1 解不等式组
3x-1 > 2x+3
x-1< 2x+1 ②
①
解不等式组
分析
上页
下页
例1 解不等式组的 详细解题过程
①
3x-1 > 2x+3
x-1< 2x+1 ②
解:
由① ,得
由② ,得
x > 4
x > -2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
x > 4
前一步
后一步
Page Up
Page Down
上页
下页
(同大取大)
例2 解不等式组
x+3 ≤ 6
①
解:
解不等式① ,得
解不等式② ,得
x ≤ 3
x <1
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
②
x <1
2x+7
<
前一步
后一步
Page Up
Page Down
上页
下页
x+8
(同小取小)
例3 解不等式组
2x+3 <5
3x-2 >4 ②
①
解:
解不等式① ,得
解不等式② ,得
x < 1
x > 2
在数轴上表示不等式①,②的解集
所以,原不等式组无解
(观察:数轴上有无公共部分)
前一步
后一步
Page Up
Page Down
上页
下页
(相背取空)
例 4 解不等式组
5x -2> 3x+3
①
解:
解不等式① ,得
解不等式② ,得
x > 2.5
x ≤ 4
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
2.5 < x ≤ 4
②
x-1
≤ 7 - x
退出
主页
前一步
后一步
Page Up
Page Down
(相对取中)
1.你能总结一下解一元一次不等式组的解题步骤吗?
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分,
也就是求出了这个不等式组的解集。
上页
下页
议一议
反馈测评
一选择题 1.选择下列不等式组的解集
上页
下页
①
x ≥ -1
x≥ 2
x≥ 2
x ≥ -1
-1≤ x≤ 2
无解
A
C
D
B
②
x< -1
x< 2
x< 2
x< -1
-1< x< 2
无解
B
D
C
A
A
无解
③
x ≥ -1
x ≥ -1
x< 2
x< 2
-1≤ x< 2
B
D
A
C
C
无解
x< -1
x< -1
④
x≥ 2
x≥ 2
-1< x≥ 2
C
B
A
D
D
B
2.不等式组
反馈测评
x +2 >0
x -1 ≥ 0
的解集在数轴上表示正确的是
3.下列不等式中,解集为x< - 4的是
x +4> 0
x +4 >0
x -5 < 0
x -5 < 0
x -5 >0
x +4 < 0
上页
下页
A
B
C
C
D
A
B
C
B
达标测评
二 . 解不等式组
2 (x+2) < x+5
3 (x-2)+8 >2x
①
②
解:
解不等式① ,得
解不等式② ,得
x < 1
x >-2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
- 2 < x<1
退出
主页
前一步
后一步
Page Up
Page Down
上页
下页
结束
小 结
(1)本节课主要学习了什么?
(2)你有什么体会?
解:设另找的木棒长为xcm,根据题意,得
10+3>x ①
10-3
探索题
7 < x <13
解不等式① ,得
x <13
解不等式② ,得
x >7
所以,原不等式组的解集是
答:第三根木棒长为
7 cm< x <13cm
一课一测(五分钟)
一.判断题:(1)
x +2 >0
y -1 ≥ 0
不是一元一次不等式组
( )
(2)
x > 3
x ≤ 5
原不等式组的解集是
3 < x < 5
( )
二.填空题:(1)满足不等式
-2 < x < 3的非零整数是______
(2)若不等式组
x>a x<b
无解,则a与b的大小关系是______
作业布置:1)课本147页复习 巩固2 2)课本148页4, 7,8
谢谢大家,欢迎提出宝贵意见!
再见!!
