人教版数学七年级下册 第七章 平面直角坐标系 复习课件(共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第七章 平面直角坐标系 复习课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 301.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 22:14:07 | ||
图片预览





文档简介
《平面直角坐标系》
复习
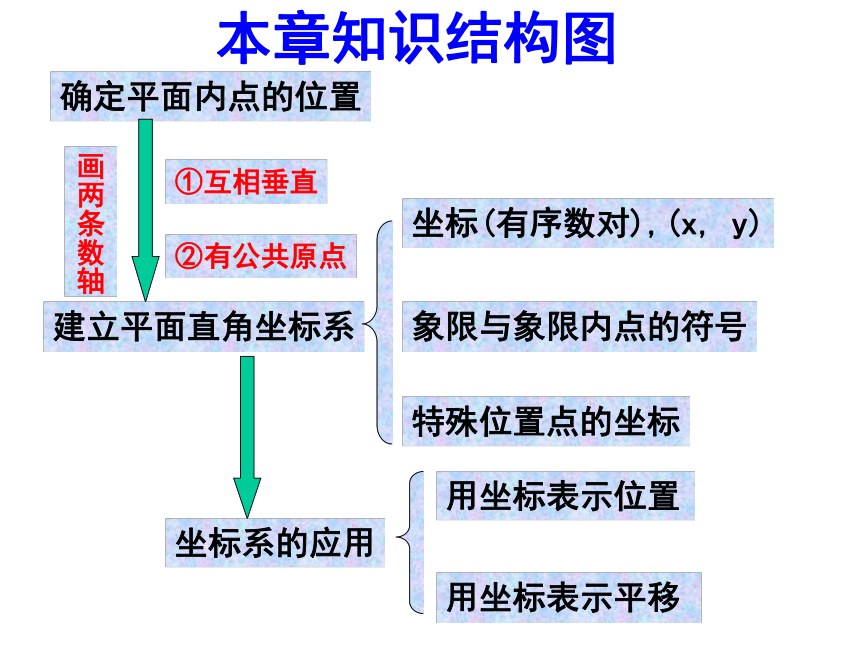
本章知识结构图
确定平面内点的位置
画两条数轴
①互相垂直
②有公共原点
建立平面直角坐标系
坐标(有序数对),(x, y)
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示位置
用坐标表示平移
垂直
重合
数轴
x轴
横轴
向右
y轴
纵轴
向上
原点
知识一:基本概念
1. 平面直角坐标系的意义及坐标平面的构成:
(1)平面内两条互相_____并且原点_____的______,组成平面直角坐标系。其中,水平的数轴称为_____或_____,习惯上取_____为正方向;竖直的数轴称为_____或_____,取_____为正方向;两坐标轴的交 点叫做平面直角坐标系的______。
0
1
-1
1
-1
x
y
2
2
-2
-2
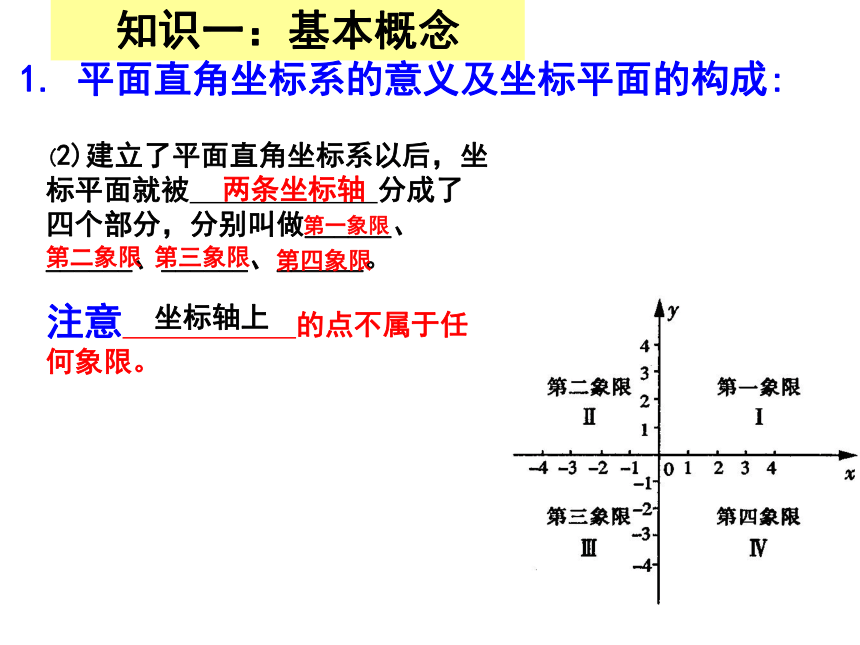
(2)建立了平面直角坐标系以后,坐标平面就被 分成了 四个部分,分别叫做______、______、______、______。
注意 的点不属于任何象限。
两条坐标轴
第一象限
第二象限
第三象限
第四象限
坐标轴上
知识一:基本概念
1. 平面直角坐标系的意义及坐标平面的构成:
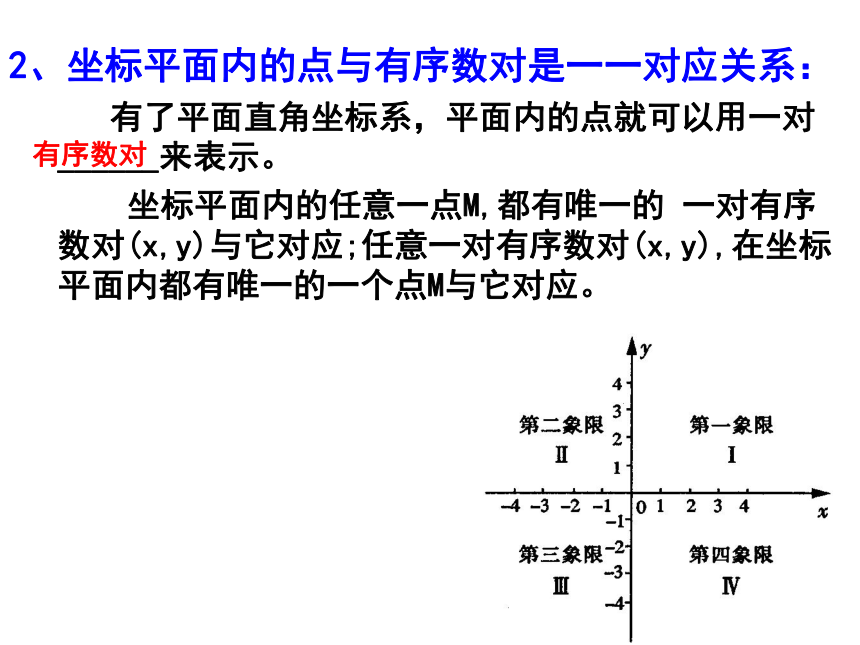
有了平面直角坐标系,平面内的点就可以用一对______来表示。
坐标平面内的任意一点M,都有唯一的 一对有序数对(x,y)与它对应;任意一对有序数对(x,y),在坐标平面内都有唯一的一个点M与它对应。
2、坐标平面内的点与有序数对是一一对应关系:
有序数对
3、坐标平面内,一般位置的点的的坐标的符号特征:
(请用“+”、“-”、“0”分别填写)
点的位置
点的横坐标符号
点的纵坐
标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴的
正半轴上
在x轴的
负半轴上
在y轴的
正半轴上
在y轴的
负半轴上
在原点
第三象限
第二象限
第一象限
第四象限
x
y
o
3
2
1
-1
-2
-3
1 2 3
-3 -2 -1
(-,+)
(-,-)
(+,-)
(+,+)
注意: 1. x轴上的点的纵坐标为0,表示为(x,0),
2. y轴上的点的横坐标为0, 表示为(0,y)。
原点既在x轴上,
又在y轴上。
2.已知mn=0,则点(m,n)在__________
3.如果点M(a+b,ab)在第二象限,那么点N(a,b)在
第_____象限
4.若点A的坐标为(a2+1, -2–b2),则点A在第____
象限.
5.若ab>0,则点p(a,b)位于第_____象限.
6.若 ,则点p(a,b)位于_____ 上.
坐标轴上
三
四
一,三
y轴(除原点)
注:判断点的位置关键抓住象限内或坐标轴上点的坐标的符号特征.
1.点P的坐标是(2,-3),则点P在第 象限;
四
【基础训练一】
7.点P(m+2,m-1)在x轴上,则点P的坐标是 .
( 3, 0 )
点P(m+2,m-1)在y轴上,则点P的坐标是 .
( 0, -3 )
9.直角坐标系中,在y轴上有一点p ,且
OP=5,则P的坐标为
(0 ,5)或(0 ,-5)
8、点P(a-1,a2-9)在x轴负半轴上,则P点坐标是 。
(-4 ,0)
【基础训练一】
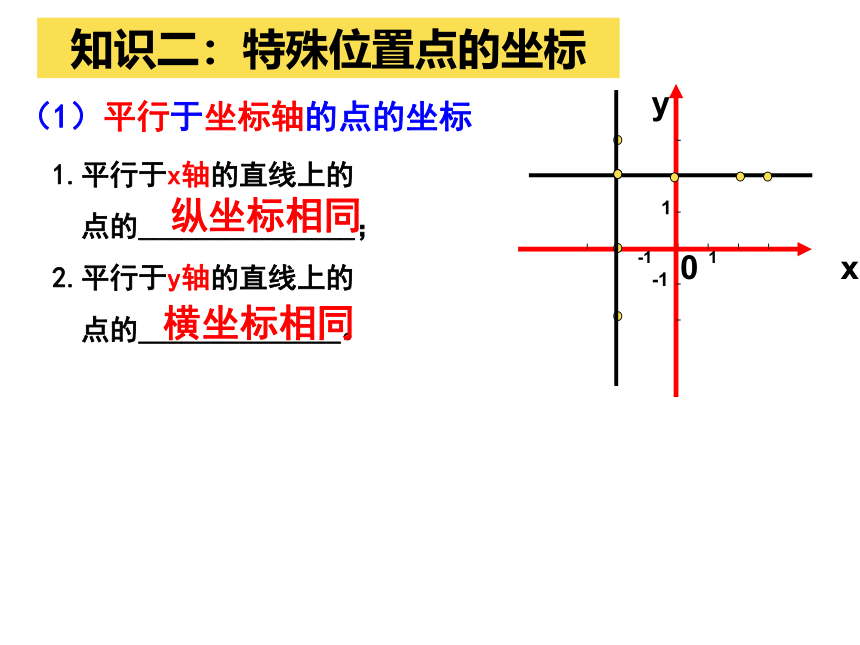
知识二:特殊位置点的坐标
(1)平行于坐标轴的点的坐标
1.平行于x轴的直线上的
点的_______________;
2.平行于y轴的直线上的
点的______________。
0
1
-1
1
-1
x
y
纵坐标相同
横坐标相同
知识二:特殊位置点的坐标
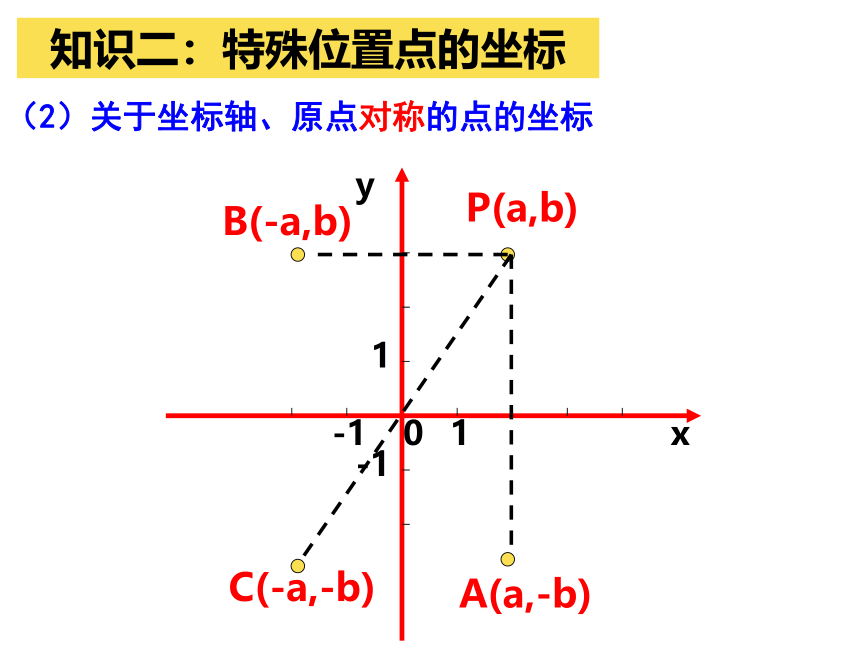
(2)关于坐标轴、原点对称的点的坐标
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
知识二:特殊位置点的坐标
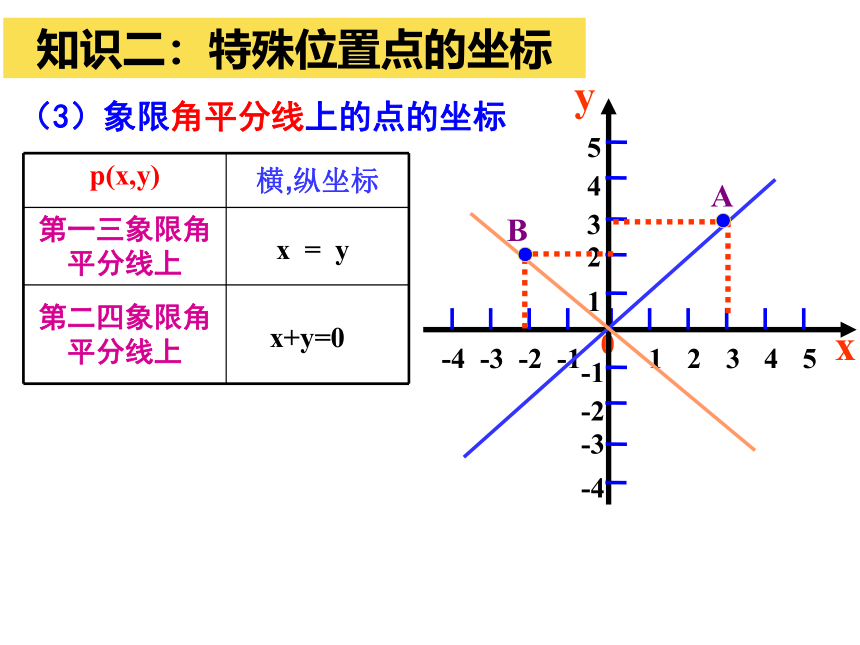
(3)象限角平分线上的点的坐标
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
x
y
A
B
p(x,y)
横,纵坐标
第一三象限角平分线上
第二四象限角平分线上
x = y
x+y=0
知识二:特殊位置点的坐标
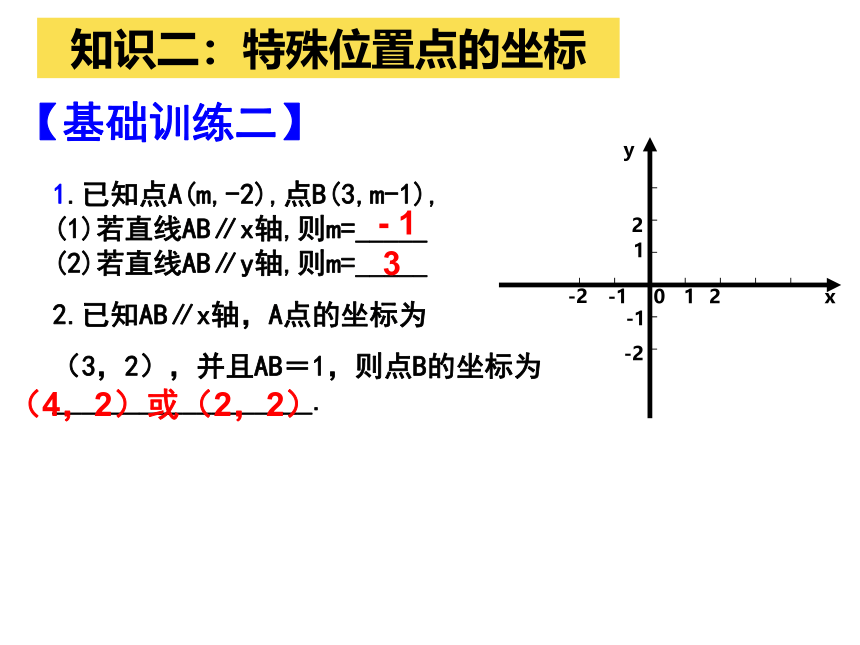
【基础训练二】
1.已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_____
2.已知AB∥x轴,A点的坐标为
(3,2),并且AB=1,则点B的坐标为__________________.
- 1
3
(4,2)或(2,2)
0
1
-1
1
-1
x
y
2
2
-2
-2
知识二:特殊位置点的坐标
5.若点(a,b)关于y轴的对称点在第二象限,则a 0,b 0.
>
<
6.如果点M(1-x,1-y)在第二象限,那么N(1-x,y-1)关于原点的对称点P在第 象限.
一
3.点(4,3)与点(4,- 3)的关系是 .
4.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( )
A.- 2 B.2 C.1 D.- 1
关于 x轴对称
B
【基础训练二】
0
1
-1
1
-1
x
y
2
2
-2
-2
知识二:特殊位置点的坐标
7.已知点A(3a+5,4a-3)在第一三象限角平分线上,则a= .
8.已知点A(3-m,2m-5)在第二四象限角平分线上,则m= .
8
2
0
1
-1
1
-1
x
y
2
2
-2
-2
【基础训练二】
知识点三:点到坐标轴的距离
1.点A(x,y)到x轴的距离为 ;
点A(x,y)到y轴的距离为 ;
2.点A(x1,0)到点B(x2,0)的距离为 ;
点A(0,y1)到点B(0,y2)的距离为 。
1.点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 。
3
4
2. 点C到x轴的距离为1,到y轴的距离为3,则C点坐标
是__________________________________.
(3,1) 或(-3,1)或 (-3,-1)或 (3,-1)
(-3,-1)
【基础训练三】
3. 第二象限点A到x轴的距离为2,到y轴的距离为5,则A点坐标是__________.
(-5,2)
4. y轴左侧点B到x轴的距离为2,到y轴的距离为5,则B点坐标是 .
(-5,2)或(-5,-2)
知识点三:点到坐标轴的距离
6.已知点P(-2,2),Q(n,2)且PQ=6,则n=________
5.已知点P(-2,3),Q(4,3)线段PQ=_________
6
4或-8
知识点三:点到坐标轴的距离
【基础训练三】
利用平面直角坐标系绘制某一区域的各点分布情况的平面图包括以下过程:
(1)建立适当的坐标系,即选择一个 为原点,确定x轴、y轴的 ; (注重寻找最佳位置)
(2)根据具体问题确定 ,选择适当的位置标出比例尺和在数轴上标出单位长度;
(3)在坐标平面内画出各点,写出各点的 和各个地点的 。
适当的参照点
正方向
单位长度
坐标
名称
知识点四:用坐标表示地理位置
【基础训练四】
1.下图是某地区的简图(图中小正方形的边长代表100 m长),请建立适当的平面直角坐标系,并写出各地点的坐标.
商场
小卖部
学校
医院
宾馆
火车站
文化宫
体育馆
基础训练四
知识点四:用坐标表示地理位置
商场
小卖部
学校
医院
宾馆
火车站
文化宫
体育馆
200
400
600
600
400
200
-200
-400
-200
-400
y
x
解:以火车站为原点,东西向为横轴,建立如图所示的坐标系.
2.如图,如果 所在位置的坐标为(-1,-2),
所在的位置的坐标为(2,-2),那么 所在的位
置的坐标为______
士
相
炮
炮
士
帅
相
┍
┕
┐
┙
┍
┕
┐
┙
x
y
(- 3,1)
0
在平面直角坐标系中,将点(x, y)向右 平移a个单位长度,可以得到对应点___________
___________.将点(x, y)向上________平移b个单位长度,可以得到对应点________________
(或向左)
(或(x-a,y))
或(x,y-b))
(或向下)
(x+a,y)
(x,y+b)
可以简单地理解为:
左、右平移___坐标不变, ___坐标变,变化规律是___减___加, 上下平移___坐标不变, ___坐标变, 变化规律是___减 ___加。
知识点五:用坐标表示图形的平移
纵
横
左
右
横
纵
下
上
3.一张脸谱经过平移,左眼A(1,3)移到A1(-3,-1)的位置,右眼B移到B1(- 1,- 1)的位置,那么B的坐标为_____
1.将点A(-1,5)先向右平移2个单位长度得到点B,
则点B的坐标为______,然后再向下平移3个单
位长度得到点C,则点C的坐标为_______.
2.把点A(2,-3)平移到点B(- 4,-2),按同样的方式,把点C(3,1)平移到点D,则点D的坐标是_____
(1,5)
(1,2)
(- 3,2)
(3,3)
知识点五:用坐标表示图形的平移
【基础训练五】
0
x
y
4.已知平面直角坐标系内点P的坐标为(-1,3),如果
将平面直角坐标系向左平移3个单位,再向下平
移2个单位,那么平移后点P的坐标为________.
(-1,3)
(2,5)
0
x
y
1.如图,求△ABC的面积
A(3,5)
B(7,3)
E
0 C(0,0)
D
知识点六:面积问题
x
y
7
5
A(-2,8)
y
x
0
D
B( -11,6)
C(- 14,0)
2.如图,四边形ABCD各个顶点的坐标如图,
(1)请确定这个四边形的面积.
(2)如果把原来ABCD各个顶点纵坐标都加上2,而横坐标保持不变所得的四边形面积是多少?
(1) 80
(2) 80
1.同桌谈收获
2.小组内说说你的困惑
3.给老师说你还有什么疑问
【颗粒归仓】
1.下列说法不正确的是( )
A.若x+y=0,则点P(x,y)一定在第二.四象限角平分线上
B.在x轴上的点纵坐标为0.
C.点P(-1,3)到y轴的距离是1.
D.点A(-a2 -1,|b|)一定在第二象限
3.已知点A(1,2),AC∥X轴, AC=5,则点C的坐标
是 _____________.
2.已知点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,则点P的坐标是 _____________.
【课堂检测】
4.若点A(a -9,a+2)在y轴负半轴上,则a=______.
5.当b=______时,点B(3, b-1)在第一.三象限角平分线上.
6.已知点A(2a+4b,-4)和点B(8,3a+2b)关于x轴对称,那么a+b= ;
7.把点A(3,2)向左平移6个单位长度得点B( ),再向下平移4个单位长度得到C ( ), .
8.若点A(m,-2),B(1,n)关于原点对称,则m= ,n= .
9.如图:(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个单位长度,再向下平移
4个单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A
B
C
A1
B1
C1
A2
B2
C2
复习
本章知识结构图
确定平面内点的位置
画两条数轴
①互相垂直
②有公共原点
建立平面直角坐标系
坐标(有序数对),(x, y)
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示位置
用坐标表示平移
垂直
重合
数轴
x轴
横轴
向右
y轴
纵轴
向上
原点
知识一:基本概念
1. 平面直角坐标系的意义及坐标平面的构成:
(1)平面内两条互相_____并且原点_____的______,组成平面直角坐标系。其中,水平的数轴称为_____或_____,习惯上取_____为正方向;竖直的数轴称为_____或_____,取_____为正方向;两坐标轴的交 点叫做平面直角坐标系的______。
0
1
-1
1
-1
x
y
2
2
-2
-2
(2)建立了平面直角坐标系以后,坐标平面就被 分成了 四个部分,分别叫做______、______、______、______。
注意 的点不属于任何象限。
两条坐标轴
第一象限
第二象限
第三象限
第四象限
坐标轴上
知识一:基本概念
1. 平面直角坐标系的意义及坐标平面的构成:
有了平面直角坐标系,平面内的点就可以用一对______来表示。
坐标平面内的任意一点M,都有唯一的 一对有序数对(x,y)与它对应;任意一对有序数对(x,y),在坐标平面内都有唯一的一个点M与它对应。
2、坐标平面内的点与有序数对是一一对应关系:
有序数对
3、坐标平面内,一般位置的点的的坐标的符号特征:
(请用“+”、“-”、“0”分别填写)
点的位置
点的横坐标符号
点的纵坐
标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴的
正半轴上
在x轴的
负半轴上
在y轴的
正半轴上
在y轴的
负半轴上
在原点
第三象限
第二象限
第一象限
第四象限
x
y
o
3
2
1
-1
-2
-3
1 2 3
-3 -2 -1
(-,+)
(-,-)
(+,-)
(+,+)
注意: 1. x轴上的点的纵坐标为0,表示为(x,0),
2. y轴上的点的横坐标为0, 表示为(0,y)。
原点既在x轴上,
又在y轴上。
2.已知mn=0,则点(m,n)在__________
3.如果点M(a+b,ab)在第二象限,那么点N(a,b)在
第_____象限
4.若点A的坐标为(a2+1, -2–b2),则点A在第____
象限.
5.若ab>0,则点p(a,b)位于第_____象限.
6.若 ,则点p(a,b)位于_____ 上.
坐标轴上
三
四
一,三
y轴(除原点)
注:判断点的位置关键抓住象限内或坐标轴上点的坐标的符号特征.
1.点P的坐标是(2,-3),则点P在第 象限;
四
【基础训练一】
7.点P(m+2,m-1)在x轴上,则点P的坐标是 .
( 3, 0 )
点P(m+2,m-1)在y轴上,则点P的坐标是 .
( 0, -3 )
9.直角坐标系中,在y轴上有一点p ,且
OP=5,则P的坐标为
(0 ,5)或(0 ,-5)
8、点P(a-1,a2-9)在x轴负半轴上,则P点坐标是 。
(-4 ,0)
【基础训练一】
知识二:特殊位置点的坐标
(1)平行于坐标轴的点的坐标
1.平行于x轴的直线上的
点的_______________;
2.平行于y轴的直线上的
点的______________。
0
1
-1
1
-1
x
y
纵坐标相同
横坐标相同
知识二:特殊位置点的坐标
(2)关于坐标轴、原点对称的点的坐标
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
C(-a,-b)
知识二:特殊位置点的坐标
(3)象限角平分线上的点的坐标
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
x
y
A
B
p(x,y)
横,纵坐标
第一三象限角平分线上
第二四象限角平分线上
x = y
x+y=0
知识二:特殊位置点的坐标
【基础训练二】
1.已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_____
2.已知AB∥x轴,A点的坐标为
(3,2),并且AB=1,则点B的坐标为__________________.
- 1
3
(4,2)或(2,2)
0
1
-1
1
-1
x
y
2
2
-2
-2
知识二:特殊位置点的坐标
5.若点(a,b)关于y轴的对称点在第二象限,则a 0,b 0.
>
<
6.如果点M(1-x,1-y)在第二象限,那么N(1-x,y-1)关于原点的对称点P在第 象限.
一
3.点(4,3)与点(4,- 3)的关系是 .
4.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( )
A.- 2 B.2 C.1 D.- 1
关于 x轴对称
B
【基础训练二】
0
1
-1
1
-1
x
y
2
2
-2
-2
知识二:特殊位置点的坐标
7.已知点A(3a+5,4a-3)在第一三象限角平分线上,则a= .
8.已知点A(3-m,2m-5)在第二四象限角平分线上,则m= .
8
2
0
1
-1
1
-1
x
y
2
2
-2
-2
【基础训练二】
知识点三:点到坐标轴的距离
1.点A(x,y)到x轴的距离为 ;
点A(x,y)到y轴的距离为 ;
2.点A(x1,0)到点B(x2,0)的距离为 ;
点A(0,y1)到点B(0,y2)的距离为 。
1.点A(2,3)到x轴的距离为 ;点B(-4,0)到y轴的距离为 ;点C到x轴的距离为1,到y轴的距离为3,且在第三象限,则C点坐标是 。
3
4
2. 点C到x轴的距离为1,到y轴的距离为3,则C点坐标
是__________________________________.
(3,1) 或(-3,1)或 (-3,-1)或 (3,-1)
(-3,-1)
【基础训练三】
3. 第二象限点A到x轴的距离为2,到y轴的距离为5,则A点坐标是__________.
(-5,2)
4. y轴左侧点B到x轴的距离为2,到y轴的距离为5,则B点坐标是 .
(-5,2)或(-5,-2)
知识点三:点到坐标轴的距离
6.已知点P(-2,2),Q(n,2)且PQ=6,则n=________
5.已知点P(-2,3),Q(4,3)线段PQ=_________
6
4或-8
知识点三:点到坐标轴的距离
【基础训练三】
利用平面直角坐标系绘制某一区域的各点分布情况的平面图包括以下过程:
(1)建立适当的坐标系,即选择一个 为原点,确定x轴、y轴的 ; (注重寻找最佳位置)
(2)根据具体问题确定 ,选择适当的位置标出比例尺和在数轴上标出单位长度;
(3)在坐标平面内画出各点,写出各点的 和各个地点的 。
适当的参照点
正方向
单位长度
坐标
名称
知识点四:用坐标表示地理位置
【基础训练四】
1.下图是某地区的简图(图中小正方形的边长代表100 m长),请建立适当的平面直角坐标系,并写出各地点的坐标.
商场
小卖部
学校
医院
宾馆
火车站
文化宫
体育馆
基础训练四
知识点四:用坐标表示地理位置
商场
小卖部
学校
医院
宾馆
火车站
文化宫
体育馆
200
400
600
600
400
200
-200
-400
-200
-400
y
x
解:以火车站为原点,东西向为横轴,建立如图所示的坐标系.
2.如图,如果 所在位置的坐标为(-1,-2),
所在的位置的坐标为(2,-2),那么 所在的位
置的坐标为______
士
相
炮
炮
士
帅
相
┍
┕
┐
┙
┍
┕
┐
┙
x
y
(- 3,1)
0
在平面直角坐标系中,将点(x, y)向右 平移a个单位长度,可以得到对应点___________
___________.将点(x, y)向上________平移b个单位长度,可以得到对应点________________
(或向左)
(或(x-a,y))
或(x,y-b))
(或向下)
(x+a,y)
(x,y+b)
可以简单地理解为:
左、右平移___坐标不变, ___坐标变,变化规律是___减___加, 上下平移___坐标不变, ___坐标变, 变化规律是___减 ___加。
知识点五:用坐标表示图形的平移
纵
横
左
右
横
纵
下
上
3.一张脸谱经过平移,左眼A(1,3)移到A1(-3,-1)的位置,右眼B移到B1(- 1,- 1)的位置,那么B的坐标为_____
1.将点A(-1,5)先向右平移2个单位长度得到点B,
则点B的坐标为______,然后再向下平移3个单
位长度得到点C,则点C的坐标为_______.
2.把点A(2,-3)平移到点B(- 4,-2),按同样的方式,把点C(3,1)平移到点D,则点D的坐标是_____
(1,5)
(1,2)
(- 3,2)
(3,3)
知识点五:用坐标表示图形的平移
【基础训练五】
0
x
y
4.已知平面直角坐标系内点P的坐标为(-1,3),如果
将平面直角坐标系向左平移3个单位,再向下平
移2个单位,那么平移后点P的坐标为________.
(-1,3)
(2,5)
0
x
y
1.如图,求△ABC的面积
A(3,5)
B(7,3)
E
0 C(0,0)
D
知识点六:面积问题
x
y
7
5
A(-2,8)
y
x
0
D
B( -11,6)
C(- 14,0)
2.如图,四边形ABCD各个顶点的坐标如图,
(1)请确定这个四边形的面积.
(2)如果把原来ABCD各个顶点纵坐标都加上2,而横坐标保持不变所得的四边形面积是多少?
(1) 80
(2) 80
1.同桌谈收获
2.小组内说说你的困惑
3.给老师说你还有什么疑问
【颗粒归仓】
1.下列说法不正确的是( )
A.若x+y=0,则点P(x,y)一定在第二.四象限角平分线上
B.在x轴上的点纵坐标为0.
C.点P(-1,3)到y轴的距离是1.
D.点A(-a2 -1,|b|)一定在第二象限
3.已知点A(1,2),AC∥X轴, AC=5,则点C的坐标
是 _____________.
2.已知点P在第四象限,点P到x轴的距离为2,到y轴的距离是3,则点P的坐标是 _____________.
【课堂检测】
4.若点A(a -9,a+2)在y轴负半轴上,则a=______.
5.当b=______时,点B(3, b-1)在第一.三象限角平分线上.
6.已知点A(2a+4b,-4)和点B(8,3a+2b)关于x轴对称,那么a+b= ;
7.把点A(3,2)向左平移6个单位长度得点B( ),再向下平移4个单位长度得到C ( ), .
8.若点A(m,-2),B(1,n)关于原点对称,则m= ,n= .
9.如图:(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个单位长度,再向下平移
4个单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A
B
C
A1
B1
C1
A2
B2
C2
