人教版数学七年级下册第8章8.3.2实际问题与二元一次方程组课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册第8章8.3.2实际问题与二元一次方程组课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 787.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
人教版初中数学七年级下册
驶向胜利的彼岸
§8.3实际问题与二元一次方程组(3)
知识导入:
经调查,某小组6个人5天共吃了90个馒头,
问:平均每人每天吃多少个馒头?
90 ÷6 ÷5=
3个/(人·天)
1人1天吃3个馒头
2.把2吨货物从A地运到100千米外的B地,共支付运费300元。问:运1吨的货物行驶1千米,需要支付多少钱?
1.5元/(吨·千米)
300 ÷100 ÷2=
运1吨货物行驶1千米需1.5元
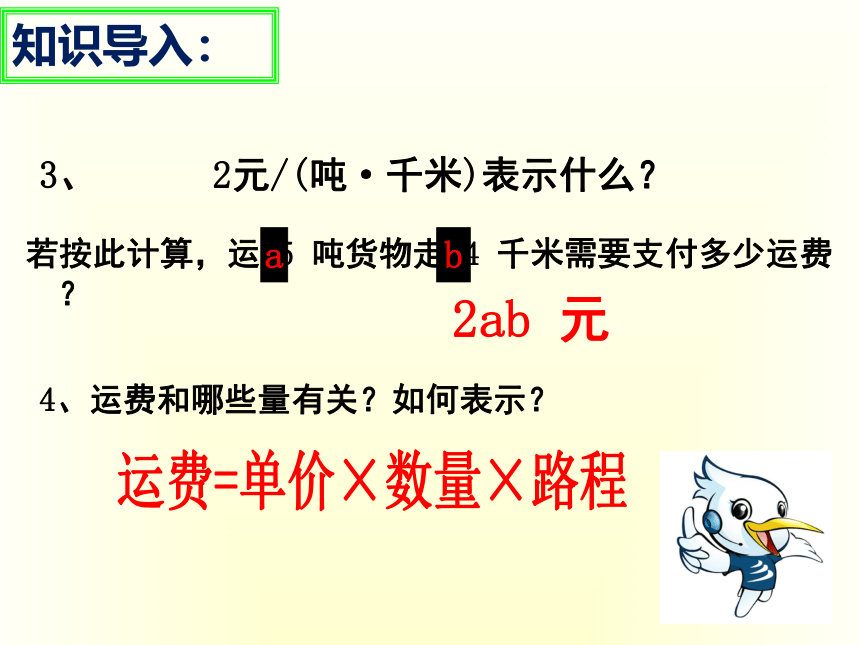
3、 2元/(吨·千米)表示什么?
若按此计算,运 5 吨货物走 4 千米需要支付多少运费?
a
b
4、运费和哪些量有关?如何表示?
知识导入:
2ab 元
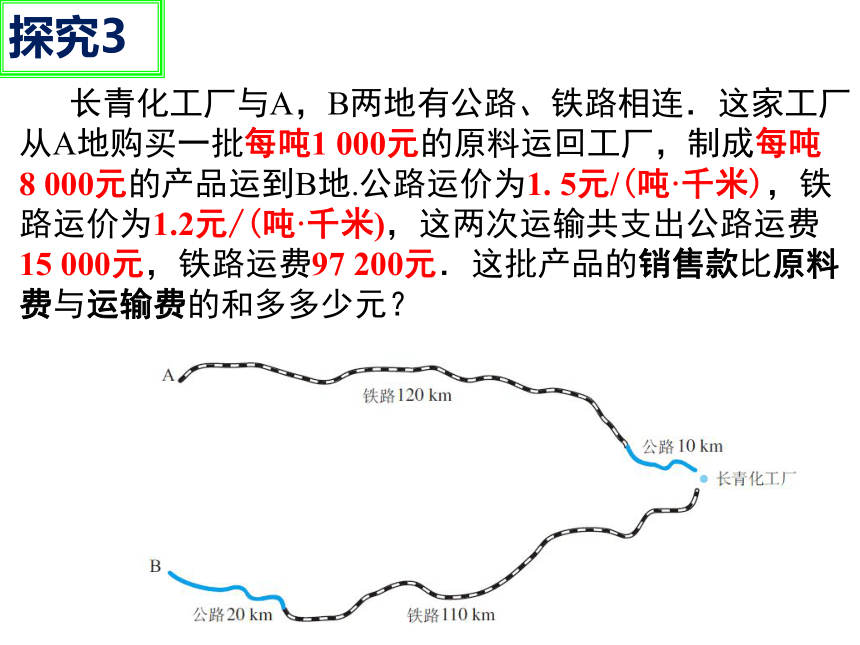
长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨
8 000元的产品运到B地.公路运价为1. 5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
探究3
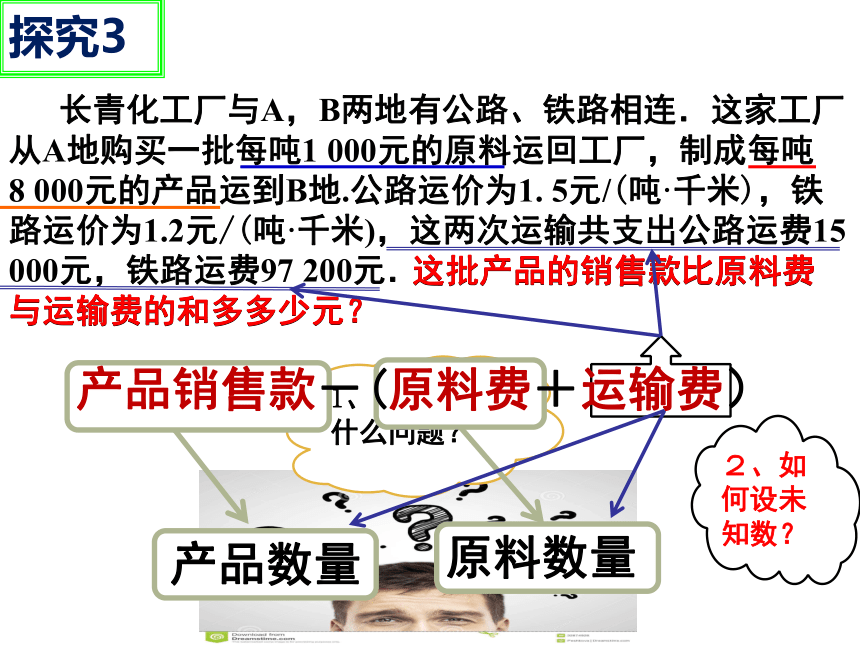
1、我们要解决什么问题?
长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨
8 000元的产品运到B地.公路运价为1. 5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.
这批产品的销售款比原料费与运输费的和多多少元?
这批产品的销售款比原料费与运输费的和多多少元?
产品数量
原料数量
产品销售款-(原料费+运输费)
2、如何设未知数?
探究3
买原料:
卖产品:
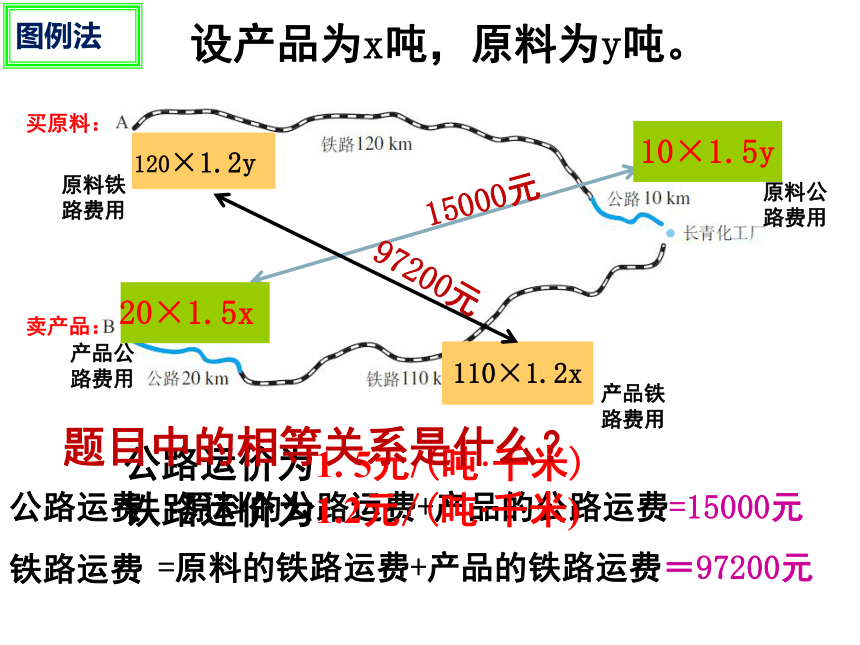
设产品为x吨,原料为y吨。
=原料的铁路运费+产品的铁路运费=97200元
铁路运费
=原料的公路运费+产品的公路运费=15000元
公路运费
15000元
图例法
公路运价为1. 5元/(吨·千米)
铁路运价为1.2元/(吨·千米)
题目中的相等关系是什么?
10×1.5y
原料公路费用
120×1.2y
原料铁路费用
20×1.5x
产品公路费用
110×1.2x
产品铁路费用
97200元
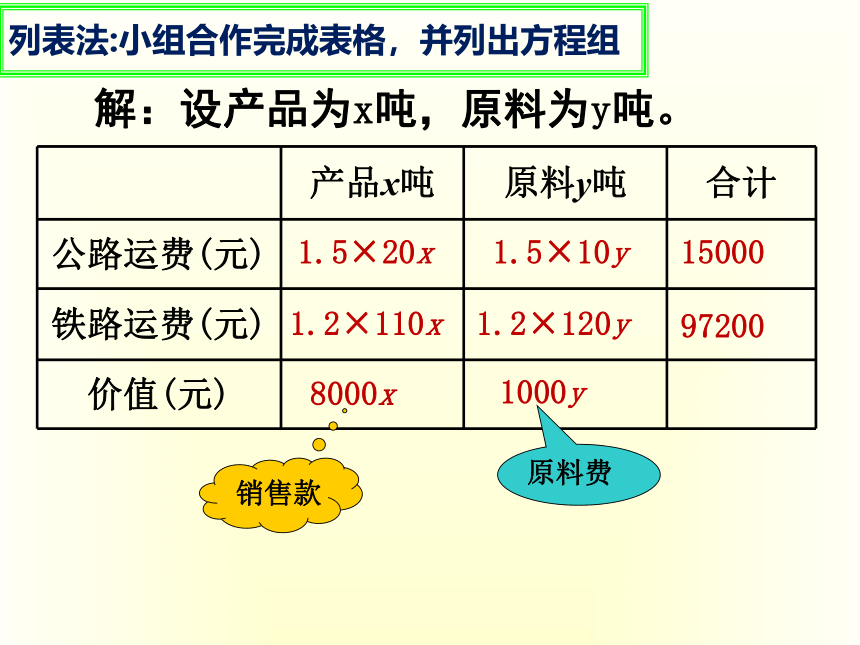
列表法:小组合作完成表格,并列出方程组
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
解:设产品为x吨,原料为y吨。
1.5×20x
1.2×110x
1.5×10y
1.2×120y
15000
97200
8000x
1000y
销售款
原料费
解得 :
8000X300=
1000X400=
15000+97200=
销售款为:
原料费为:
运输费为:
所以销售款比原料费与运输费的和多:
答:销售款比原料费与运输费的和多1887800元。
解:设产品为x吨,原料为y吨。
2400000 - (400000+112200)=
1887800(元)
2400000(元)
400000(元)
112200(元)
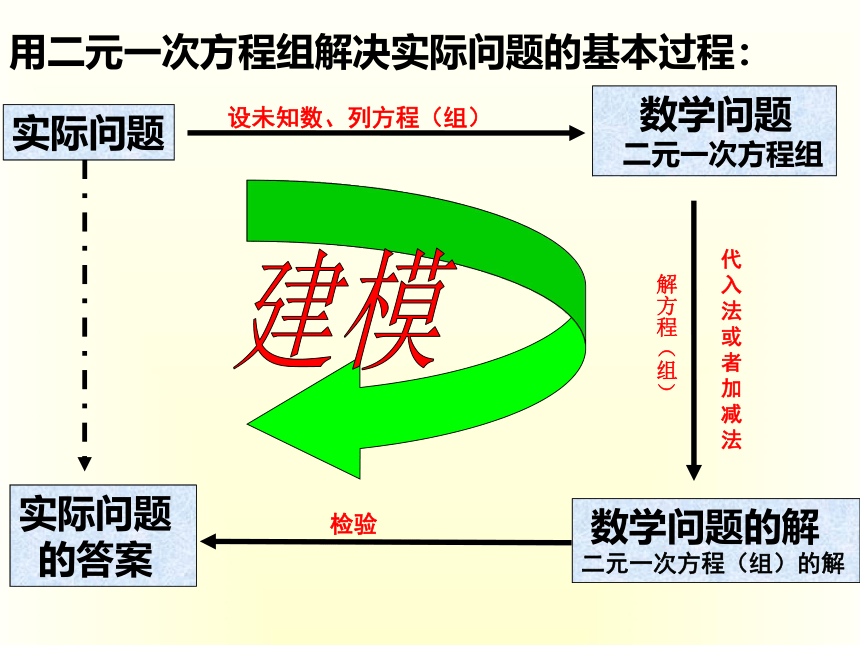
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
数学问题的解
二元一次方程(组)的解
检验
实际问题
的答案
用二元一次方程组解决实际问题的基本过程:
代入法或者加减法
解方程(组)
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
学以致用:教材P102第6题
解:设甲到乙上坡路长为x千米,平路长为y千米
X
5
X
3
y
4
y
4
甲
乙
3km/h
54分
4km/h
乙
5km/h
42分
甲
4km/h
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
上坡
平路
下坡
合计
甲到乙时间
乙到甲时间
解:设甲到乙上坡路长为x千米,平路长为y千米
上坡
平路
下坡
合计
甲到乙时间
乙到甲时间
X
5
54
60
X
3
解:设甲到乙上坡路长为x千米,平路长为y千米
由题意得:
42
60
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
y
4
y
4
解:设甲到乙上坡路长为x千米,平路长为y千米,
由题意得:
解得:
X=1.5
y =1.6
答:甲地到乙地全程是3.1千米。
∴x+y=1.5+1.6=3.1(千米)
解法示范:
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
北京和上海都有某种仪器可供外地使用。其中
北京可提供10台,上海可提供4台。已知重庆需要8台,
武汉需要6台,从北京、上海将仪器运往重庆、武汉
的费用如下表所示。有关部门计划用8000元运送这
些仪器,请你设计一种方案,使武汉、重庆能得到
所需仪器,而且运费正好够用。
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
思考与探究:
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
300元
800元
500元
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
300元
800元
8台
2台
4台
费用:8×800+2×400+4 ×300=8400元>8000元
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
800元
500元
费用:4×800+6×400+4×500=7600元<8000元
6台
4台
4台
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
300元
800元
X台
500元
y台
(4-y)台
(10-X)台
800x元
500y元
400(10-x)元
300(4-y )元
解:设北京运往重庆x台,上海运往重庆y台,
{
800x+400(10-x)+500y+300(4-y)=8000
x+y=8
解这个方程组,得
x = 6
y = 2
{
答:北京运往重庆6台,运往武汉4台;
上海运往重庆2台,运往武汉2台。
由题意得:
∴10-x=10-6=4(台)
4-y=4-2=2(台)
课堂小结:
1、利用二元一次方程组解实际问题的一般步骤:
审、设、列、解、验、答
2、这节课我们主要探究了二元一次方程组在道路运输问题中的应用。这类问题,往往涉及到的量很多,关系也比较复杂。这就特别需要一些有效的方式来帮助我们处理信息,帮助我们寻找问题中的相等关系。图表法就是我们得力的助手,它以简洁直观的形象向我们揭示了纷繁复杂的量与量之间的关系,是我们解题的好帮手。
课后作业:
2、延伸拓展:甲、乙两人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4分钟后两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙两人的速度及环形场地的周长。
1、教材P111第6题:甲、乙两人都以不变的速度在环形路上跑步,如果同时同地出发,反向而行,每隔2分钟相遇一次;如果同时同地出发,同向而行,每隔6分钟相遇一次。已知甲比乙跑得快,甲、乙二人每分各跑多少圈?
再见!
驶向胜利的彼岸
§8.3实际问题与二元一次方程组(3)
知识导入:
经调查,某小组6个人5天共吃了90个馒头,
问:平均每人每天吃多少个馒头?
90 ÷6 ÷5=
3个/(人·天)
1人1天吃3个馒头
2.把2吨货物从A地运到100千米外的B地,共支付运费300元。问:运1吨的货物行驶1千米,需要支付多少钱?
1.5元/(吨·千米)
300 ÷100 ÷2=
运1吨货物行驶1千米需1.5元
3、 2元/(吨·千米)表示什么?
若按此计算,运 5 吨货物走 4 千米需要支付多少运费?
a
b
4、运费和哪些量有关?如何表示?
知识导入:
2ab 元
长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨
8 000元的产品运到B地.公路运价为1. 5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
探究3
1、我们要解决什么问题?
长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨
8 000元的产品运到B地.公路运价为1. 5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15 000元,铁路运费97 200元.
这批产品的销售款比原料费与运输费的和多多少元?
这批产品的销售款比原料费与运输费的和多多少元?
产品数量
原料数量
产品销售款-(原料费+运输费)
2、如何设未知数?
探究3
买原料:
卖产品:
设产品为x吨,原料为y吨。
=原料的铁路运费+产品的铁路运费=97200元
铁路运费
=原料的公路运费+产品的公路运费=15000元
公路运费
15000元
图例法
公路运价为1. 5元/(吨·千米)
铁路运价为1.2元/(吨·千米)
题目中的相等关系是什么?
10×1.5y
原料公路费用
120×1.2y
原料铁路费用
20×1.5x
产品公路费用
110×1.2x
产品铁路费用
97200元
列表法:小组合作完成表格,并列出方程组
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
解:设产品为x吨,原料为y吨。
1.5×20x
1.2×110x
1.5×10y
1.2×120y
15000
97200
8000x
1000y
销售款
原料费
解得 :
8000X300=
1000X400=
15000+97200=
销售款为:
原料费为:
运输费为:
所以销售款比原料费与运输费的和多:
答:销售款比原料费与运输费的和多1887800元。
解:设产品为x吨,原料为y吨。
2400000 - (400000+112200)=
1887800(元)
2400000(元)
400000(元)
112200(元)
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
数学问题的解
二元一次方程(组)的解
检验
实际问题
的答案
用二元一次方程组解决实际问题的基本过程:
代入法或者加减法
解方程(组)
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
学以致用:教材P102第6题
解:设甲到乙上坡路长为x千米,平路长为y千米
X
5
X
3
y
4
y
4
甲
乙
3km/h
54分
4km/h
乙
5km/h
42分
甲
4km/h
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
上坡
平路
下坡
合计
甲到乙时间
乙到甲时间
解:设甲到乙上坡路长为x千米,平路长为y千米
上坡
平路
下坡
合计
甲到乙时间
乙到甲时间
X
5
54
60
X
3
解:设甲到乙上坡路长为x千米,平路长为y千米
由题意得:
42
60
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
y
4
y
4
解:设甲到乙上坡路长为x千米,平路长为y千米,
由题意得:
解得:
X=1.5
y =1.6
答:甲地到乙地全程是3.1千米。
∴x+y=1.5+1.6=3.1(千米)
解法示范:
从甲地到乙地的路有一段上坡与一段平路,如果保持上坡每小时行3千米,平路每小时行4千米,下坡每小时行5千米,那么从甲地到乙地需行54分钟,从乙地到甲地需行42分钟,甲地到乙地全程是多少?
北京和上海都有某种仪器可供外地使用。其中
北京可提供10台,上海可提供4台。已知重庆需要8台,
武汉需要6台,从北京、上海将仪器运往重庆、武汉
的费用如下表所示。有关部门计划用8000元运送这
些仪器,请你设计一种方案,使武汉、重庆能得到
所需仪器,而且运费正好够用。
运费表
单位:(元
/
台)
终点
起点
武汉
重庆
北京
400
800
上海
300
500
思考与探究:
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
300元
800元
500元
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
300元
800元
8台
2台
4台
费用:8×800+2×400+4 ×300=8400元>8000元
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
800元
500元
费用:4×800+6×400+4×500=7600元<8000元
6台
4台
4台
北京
上海
重庆
武汉
10台
4台
需要8台
需要6台
400元
300元
800元
X台
500元
y台
(4-y)台
(10-X)台
800x元
500y元
400(10-x)元
300(4-y )元
解:设北京运往重庆x台,上海运往重庆y台,
{
800x+400(10-x)+500y+300(4-y)=8000
x+y=8
解这个方程组,得
x = 6
y = 2
{
答:北京运往重庆6台,运往武汉4台;
上海运往重庆2台,运往武汉2台。
由题意得:
∴10-x=10-6=4(台)
4-y=4-2=2(台)
课堂小结:
1、利用二元一次方程组解实际问题的一般步骤:
审、设、列、解、验、答
2、这节课我们主要探究了二元一次方程组在道路运输问题中的应用。这类问题,往往涉及到的量很多,关系也比较复杂。这就特别需要一些有效的方式来帮助我们处理信息,帮助我们寻找问题中的相等关系。图表法就是我们得力的助手,它以简洁直观的形象向我们揭示了纷繁复杂的量与量之间的关系,是我们解题的好帮手。
课后作业:
2、延伸拓展:甲、乙两人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4分钟后两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙两人的速度及环形场地的周长。
1、教材P111第6题:甲、乙两人都以不变的速度在环形路上跑步,如果同时同地出发,反向而行,每隔2分钟相遇一次;如果同时同地出发,同向而行,每隔6分钟相遇一次。已知甲比乙跑得快,甲、乙二人每分各跑多少圈?
再见!
