人教数学七年级下册第7章7.2.2 用坐标表示平移课件(共24张PPT)
文档属性
| 名称 | 人教数学七年级下册第7章7.2.2 用坐标表示平移课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






文档简介
让心灵去旅行 ...
人生就象一场旅行
不必在乎目的地
在乎的是沿途的风景
以及,看风景的心情
学习重在过程
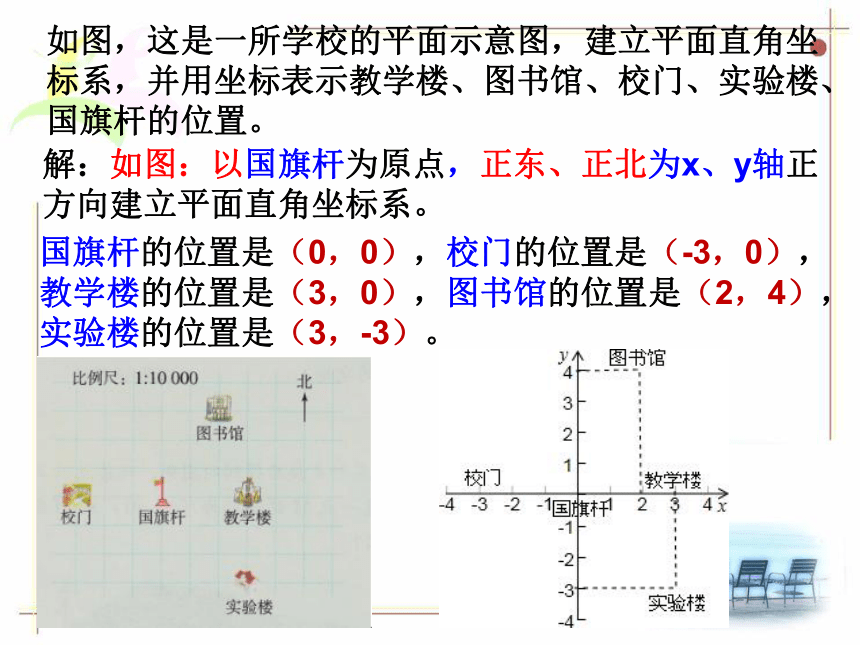
如图,这是一所学校的平面示意图,建立平面直角坐标系,并用坐标表示教学楼、图书馆、校门、实验楼、国旗杆的位置。
解:如图:以国旗杆为原点,正东、正北为x、y轴正
方向建立平面直角坐标系。
国旗杆的位置是(0,0),校门的位置是(-3,0),
教学楼的位置是(3,0),图书馆的位置是(2,4),
实验楼的位置是(3,-3)。
复习:
1、点C在x轴上方,距离x轴5个单位长度,距离y轴2个单位长度,则点C的坐标为_____ __________ 。
2、点B(3, –7)到x轴的距离是______,到y轴的距离是______ 。
3、 ⑴若点(a–4,a+1)在x轴上,则a的值是______,该点的坐标为_________。
⑵若点(a–4,a+1)在y轴上,则a的值是______,该点的坐标为_________。
(2 , 5)
或( – 2, 5)
7
3
–1
(– 5 , 0 )
4
(0 , 5 )
4、若点P(– m,n)在第二象限,则点Q(m, –n)在第______象限。
5、已知x轴上的点P到y轴的距离是5,则点P的坐标为______ 。
四
(5,0)或( – 5,0)
体 验 回 顾
1. 什么叫做平移?
2 . 平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形的位置改变,形状、大小不变。
B
A
C
A’.
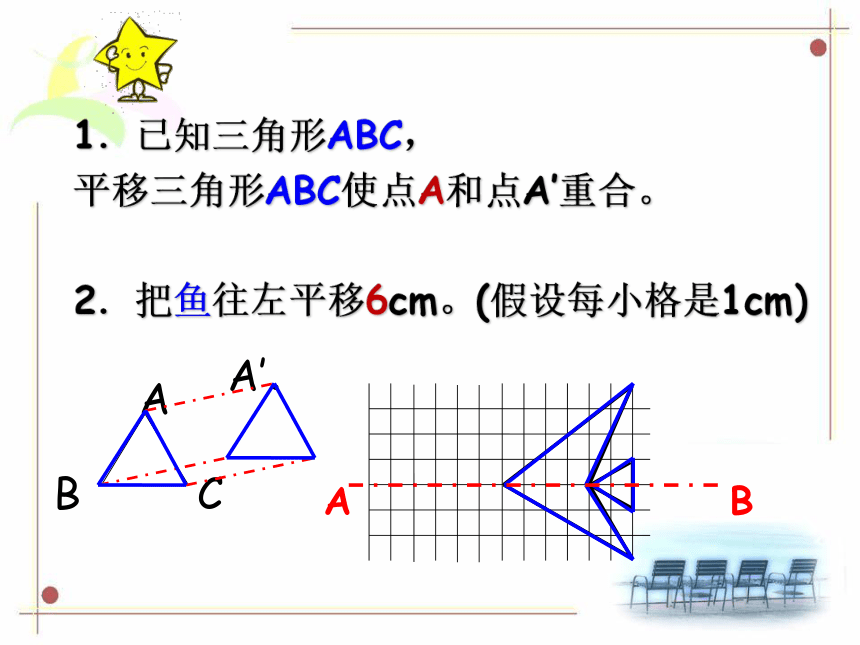
1.已知三角形ABC,
平移三角形ABC使点A和点A’重合。
2.把鱼往左平移6cm。(假设每小格是1cm)
A
B
探 究 一
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-3)
y
1、向右平移3个单位长度
2、向右平移5个单位长度
B (1,-3)
C (3,-3)
如图A (– 2, – 3)
请你观察平移前后对应点的坐标的变化,你能发现什么规律吗?
3、向左平移3个单位长度
4、向左平移5个单位长度
D (-5,-3)
E (-7,-3)
-5
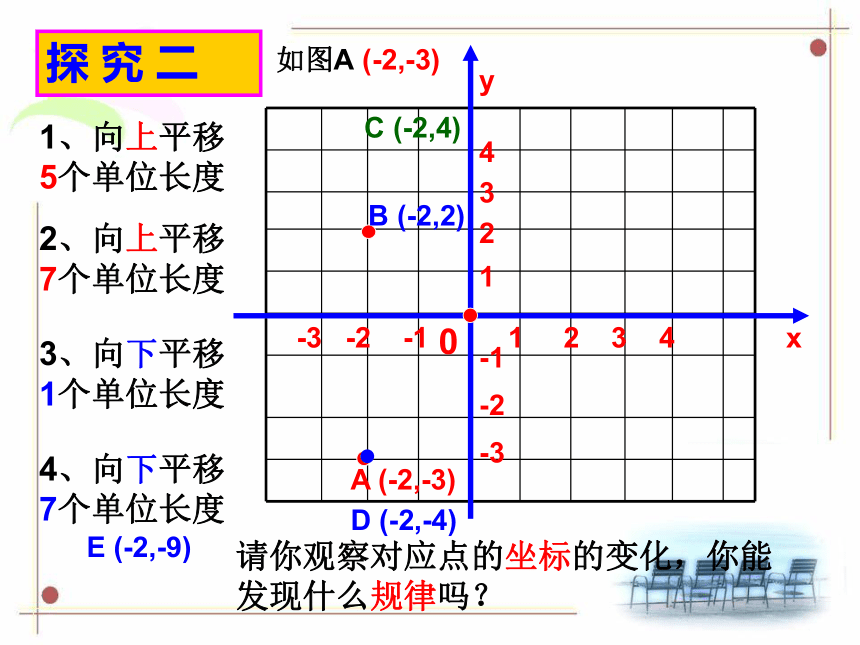
探 究 二
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-3)
y
C (-2,4)
B (-2,2)
1、向上平移5个单位长度
2、向上平移7个单位长度
请你观察对应点的坐标的变化,你能发现什么规律吗?
如图A (-2,-3)
3、向下平移1个单位长度
4、向下平移7个单位长度
D (-2,-4)
E (-2,-9)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
3.总结规律1:图形平移与点的坐标变化
间的关系
阅读课本76页探究
探究:如图4,正方形ABCD四个顶点的坐标分别是
A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H,(1)他们的坐标分别是什么?(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
解:点E,F,G,H的坐标分别是:(6,-3),(6,-4),(7,-4),(7,-3)。若直接平移正方形ABCD,使点A移到点E,它就和我们前面得到的正方形位置相同。
由图形向下平移7个单位长度,再向右平移8个单位长度,
得:
各点纵坐标减7,横坐标加8。
B(-2,3),C(-1,3),D(-1,4),
A(-2,4)→E (6,-3)
B(-2,3)→F(6,-4)
C(-1,3)→G(7,- 4)
D(-1,4)→H(7,-3)
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个
顶点的横坐标都减去6,
纵坐标不变,分别得到
点A1,B1,C1
(2)依次连接A1,B1,C1,
各点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
将△ABC三个顶点的纵坐标都减
去5,横坐标不变。分别得到点A2,B2,C2。
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和
位置上有什么关系?
1.例题探索
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
(3)将△ABC三个顶点的横坐标都减 6;纵坐标减5,又能得到什么结论?
①
②
2. 探究
总结:图形的斜向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2:
如图△ABC中任意一点P(x0,y0)经平移后对应
点为P1(x0+5,y0+3),将△ABC作同样的平移到△A1B1C1。
求A1、B1、C1的坐标 。
(2)
(2)
A1(3,6)
B1(1,4)
C1(7,3)
练习:
线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
(1,2)
练习:
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
有相距5个单位的两点 A(-3,a),B(b,4),
AB//x轴,则a= ___ ,b= ___ 。
A
B
4
2
练习:
(1)
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(3)
0
(2)
小
结
如图与(1)比较,请回答:
(2)(3)中的三角形发生了哪些变化?
图中直角三角形的顶点坐标分别了什么变化?
回顾所学
你能运用图形尽可能具体地对今天所学的知识进行一番回顾吗?
对于
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
A(-2,4)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
规律1:
图形平移与点的坐标变化间的关系
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
规律2:
www.czsx.com.cn
作业:
课本80页第10题
人生就象一场旅行
不必在乎目的地
在乎的是沿途的风景
以及,看风景的心情
学习重在过程
如图,这是一所学校的平面示意图,建立平面直角坐标系,并用坐标表示教学楼、图书馆、校门、实验楼、国旗杆的位置。
解:如图:以国旗杆为原点,正东、正北为x、y轴正
方向建立平面直角坐标系。
国旗杆的位置是(0,0),校门的位置是(-3,0),
教学楼的位置是(3,0),图书馆的位置是(2,4),
实验楼的位置是(3,-3)。
复习:
1、点C在x轴上方,距离x轴5个单位长度,距离y轴2个单位长度,则点C的坐标为_____ __________ 。
2、点B(3, –7)到x轴的距离是______,到y轴的距离是______ 。
3、 ⑴若点(a–4,a+1)在x轴上,则a的值是______,该点的坐标为_________。
⑵若点(a–4,a+1)在y轴上,则a的值是______,该点的坐标为_________。
(2 , 5)
或( – 2, 5)
7
3
–1
(– 5 , 0 )
4
(0 , 5 )
4、若点P(– m,n)在第二象限,则点Q(m, –n)在第______象限。
5、已知x轴上的点P到y轴的距离是5,则点P的坐标为______ 。
四
(5,0)或( – 5,0)
体 验 回 顾
1. 什么叫做平移?
2 . 平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形的位置改变,形状、大小不变。
B
A
C
A’.
1.已知三角形ABC,
平移三角形ABC使点A和点A’重合。
2.把鱼往左平移6cm。(假设每小格是1cm)
A
B
探 究 一
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-3)
y
1、向右平移3个单位长度
2、向右平移5个单位长度
B (1,-3)
C (3,-3)
如图A (– 2, – 3)
请你观察平移前后对应点的坐标的变化,你能发现什么规律吗?
3、向左平移3个单位长度
4、向左平移5个单位长度
D (-5,-3)
E (-7,-3)
-5
探 究 二
0
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
A (-2,-3)
y
C (-2,4)
B (-2,2)
1、向上平移5个单位长度
2、向上平移7个单位长度
请你观察对应点的坐标的变化,你能发现什么规律吗?
如图A (-2,-3)
3、向下平移1个单位长度
4、向下平移7个单位长度
D (-2,-4)
E (-2,-9)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
3.总结规律1:图形平移与点的坐标变化
间的关系
阅读课本76页探究
探究:如图4,正方形ABCD四个顶点的坐标分别是
A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H,(1)他们的坐标分别是什么?(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
解:点E,F,G,H的坐标分别是:(6,-3),(6,-4),(7,-4),(7,-3)。若直接平移正方形ABCD,使点A移到点E,它就和我们前面得到的正方形位置相同。
由图形向下平移7个单位长度,再向右平移8个单位长度,
得:
各点纵坐标减7,横坐标加8。
B(-2,3),C(-1,3),D(-1,4),
A(-2,4)→E (6,-3)
B(-2,3)→F(6,-4)
C(-1,3)→G(7,- 4)
D(-1,4)→H(7,-3)
二. 探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个
顶点的横坐标都减去6,
纵坐标不变,分别得到
点A1,B1,C1
(2)依次连接A1,B1,C1,
各点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
将△ABC三个顶点的纵坐标都减
去5,横坐标不变。分别得到点A2,B2,C2。
2
3
A2
C2
B2
1
A
C
B
A
C
B
4
x
-
3
y
1
-
1
-
2
-
4
1
2
-
1
-
2
-
3
-
4
0
猜想: △ A2B2C2与△ ABC的大小、形状和
位置上有什么关系?
1.例题探索
A(4,3) B(3,1) C(1,2)
A2(4,-2)
B2(3,-4)
C2(1,-3)
(3)将△ABC三个顶点的横坐标都减 6;纵坐标减5,又能得到什么结论?
①
②
2. 探究
总结:图形的斜向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2:
如图△ABC中任意一点P(x0,y0)经平移后对应
点为P1(x0+5,y0+3),将△ABC作同样的平移到△A1B1C1。
求A1、B1、C1的坐标 。
(2)
(2)
A1(3,6)
B1(1,4)
C1(7,3)
练习:
线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
(1,2)
练习:
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
有相距5个单位的两点 A(-3,a),B(b,4),
AB//x轴,则a= ___ ,b= ___ 。
A
B
4
2
练习:
(1)
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(3)
0
(2)
小
结
如图与(1)比较,请回答:
(2)(3)中的三角形发生了哪些变化?
图中直角三角形的顶点坐标分别了什么变化?
回顾所学
你能运用图形尽可能具体地对今天所学的知识进行一番回顾吗?
对于
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
A(-2,4)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
规律1:
图形平移与点的坐标变化间的关系
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
规律2:
www.czsx.com.cn
作业:
课本80页第10题
