沪教版(上海)初中数学九年级第一学期 24.5 相似三角形专题复习 课件(共19张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.5 相似三角形专题复习 课件(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 22:09:04 | ||
图片预览





文档简介
(共19张PPT)
相似三角形
专题复习
课前练习:
1. 根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(1) ∠A=120°,AB=7 ,AC=14 ∠A′=120°,A′B′=3 ,A′C′=6
(2) AB=4 ,BC=6 ,AC=8 A′B′=12 ,B′C′=18 ,A′C′=21
(3) ∠A=70°,∠B=48°, ∠A′=70°, ∠C′=62°
2. 在△ABC中,在△ABC中, DE∥BC,若AD:DB=1:3,DE=2, 则BC的长为( )
B
C
E
D
A
课前练习:
1、根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(1) ∠A=120°,AB=7 ,AC=14
∠A′=120°,A′B′=3 ,A′C′=6
解: △ABC∽△A′B′C′
∵
∴
∵ ∠A= ∠A′
∴ △ABC∽△A′B′C′
相似三角形的判定:
如果两个三角形的两组对应边的比相等, 并且相应的夹角相等,那么这两个三角形相似。
课前练习:
1、根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(2) AB=4 ,BC=6 ,AC= ;A′B′=12 ,B′C′=18 ,A′C′=21
解:
∵
∴
相似三角形的判定:
如果两个三角形的三组对应边的比相等
那么这两个三角形相似。
8
7
∴ △ABC∽△A′B′C′
∴ △ABC与△A′B′C′不相似
△ABC∽△A′B′C′
△ABC与△A′B′C′不相似
课前练习:
1. 根据下列条件能否判定△ABC与△A′B′C′相似?
为什么?
(3) ∠A=70°,∠B=48°, ∠A′=70°, ∠C′=62°
解:∵ ∠A=70°,∠B=48°
∴ ∠C=180°- 70°- 48°= 62°,
∴ ∠A= ∠A′ ∠C= ∠C′
∴ △ABC∽△A′B′C′
相似三角形的判定:
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
课前练习:
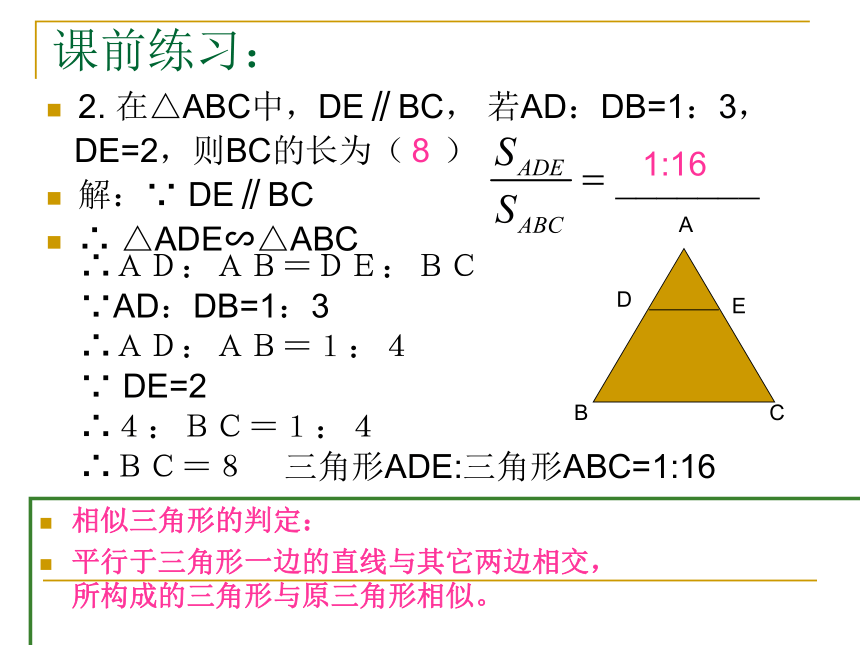
2. 在△ABC中,DE∥BC, 若AD:DB=1:3,
DE=2,则BC的长为( )
解:∵ DE∥BC
∴ △ADE∽△ABC
相似三角形的判定:
平行于三角形一边的直线与其它两边相交, 所构成的三角形与原三角形相似。
B
C
E
D
A
8
∴AD:AB=DE:BC
∵AD:DB=1:3
∴AD:AB=1:4
∵ DE=2
∴4:BC=1:4
∴BC=8 三角形ADE:三角形ABC=1:16
1:16
课前练习:
3.如图,等腰三角形ABC中,AB=AC,AD是高,BE是中线,AD、BE交于点F,BC=10,AF=8,
则AB= ( )
13
∵ 等腰三角形ABC中,AD是高,BE是中线
∴F是三角形ABC的重心
AF=2FD
∵AF=8
∴FD=4,即AD=12
∵AD⊥BC,2BD=2DC=BC
∴Rt △ABD中,AD=12,BD=5
∴由勾股定理,可得AB=13
相似三角形的判定
(1)平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似。
(2)如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
(3)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
(4)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
相似三角形的性质
(1)对应边的比相等,对应角相等
(2)相似三角形的周长比等于相似比
(3)相似三角形的面积比等于相似比的平方
(4)相似三角形的对应边上的高、中线、角平分线的比等于相似比
相似三角形的应用:
1. 利用三角形相似,可证明角相等;线 段成比例(或等积式)
2. 利用三角形相似,求线段的长等;
3. 利用三角形相似,可以解决一些不能直接测量的物体的长度。如求河的宽度、求建筑物的高度等。
课堂练习:
D是△ABC的边AB上的点, 请你添加一个条件,使△ACD与△ABC相似, 这个条件是( )
①∠ADC=∠ACB
② ∠ACD=∠B
③
如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为( )
A
D
C
B
15
课堂练习:
如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F,BE:AB=2:3,则△BEF与△CDF的周长比为( );若△BEF的面积为8平方厘米,则△CDF的面积为( )
2:3
18平方厘米
A
B
E
C
D
F
课堂练习:
如图,火焰AC通过纸板EF上的一个小孔O照射到屏幕上形成倒立的实像.像的长度BD=2cm,OA=60cm,OB=20cm,火焰AC的长是 cm.
解:由实际意义知:AC//BD,
∴ AC//BD
∴△ACO∽△OBD
∴AO:BO=AC:BD
∵AO=60m,BO=20m
∴60:20=AC:2
解得:AC=6(cm)
∴火焰长是6厘米。
6
课堂练习:
如图,阳光通过窗口照亮到室内,在地面上留下2.7m宽的亮区DE,已知亮区DE到窗口下的墙角距离EC=8.7m,窗口高AB=1.8m,那么窗口底边离地面的高BC= m
A. 4.8m B. 6.4m
C. 5.8m D. 10m
解:由实际意义知:AD//BE,
∵ AC//BD
∴CE:DE=CB:BA
∵CE=8.7m, DE=2.7m
BA=1.8m
∴8.7:2.7=CB:1.8
解得:BC=5.8(cm)
∴窗口离地面的高度BC是5.8m。
C
练一练
1. 如图,△ABD∽ △ACE
求证: △ABC ∽ △ADE
2.如图,在△ABC中,AB=AC,∠EDF=∠B,点D、E、F分别在BC、AB、AC上,
求证:BD×CD=BE×CF.
图(1)
拓展:
某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上种植花木(如图)他们想在△AMD和△BMC地带种植单价为10元 /米2的太阳花,当△AMD地带种满花后,已经花了500元,请你算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由。
拓展:
如图,在直角△ABC中,∠C=90°,AC=3㎝,BC=4㎝,设P、Q分别为AB上的动点,在点P自点A沿AB方向向点B做匀速移动的同时,点Q自点B沿BC方向向点C做匀速移动,他们移动的速度均为每秒1㎝,当点Q到达点C时,P点就停止运动。设P、Q移动的时间为t秒.
(1)写出△PBQ的面积S(cm2)与时间t(秒)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,△PBQ为等腰三角形?
(3)△PBQ能否与直角三角形ABC相似?若能,求t的值,若不能,说明理由
小结:
(1)掌握相似三角形的判定方法及性质;
(2)能灵活运用相似三角形的判定方法及性质进行计算或证明;
(3)利用相似解决一些实际问题
通这一节的复习之后你有哪些收获?
作业:
完成教学告白后的课后练习
相似三角形
专题复习
课前练习:
1. 根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(1) ∠A=120°,AB=7 ,AC=14 ∠A′=120°,A′B′=3 ,A′C′=6
(2) AB=4 ,BC=6 ,AC=8 A′B′=12 ,B′C′=18 ,A′C′=21
(3) ∠A=70°,∠B=48°, ∠A′=70°, ∠C′=62°
2. 在△ABC中,在△ABC中, DE∥BC,若AD:DB=1:3,DE=2, 则BC的长为( )
B
C
E
D
A
课前练习:
1、根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(1) ∠A=120°,AB=7 ,AC=14
∠A′=120°,A′B′=3 ,A′C′=6
解: △ABC∽△A′B′C′
∵
∴
∵ ∠A= ∠A′
∴ △ABC∽△A′B′C′
相似三角形的判定:
如果两个三角形的两组对应边的比相等, 并且相应的夹角相等,那么这两个三角形相似。
课前练习:
1、根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(2) AB=4 ,BC=6 ,AC= ;A′B′=12 ,B′C′=18 ,A′C′=21
解:
∵
∴
相似三角形的判定:
如果两个三角形的三组对应边的比相等
那么这两个三角形相似。
8
7
∴ △ABC∽△A′B′C′
∴ △ABC与△A′B′C′不相似
△ABC∽△A′B′C′
△ABC与△A′B′C′不相似
课前练习:
1. 根据下列条件能否判定△ABC与△A′B′C′相似?
为什么?
(3) ∠A=70°,∠B=48°, ∠A′=70°, ∠C′=62°
解:∵ ∠A=70°,∠B=48°
∴ ∠C=180°- 70°- 48°= 62°,
∴ ∠A= ∠A′ ∠C= ∠C′
∴ △ABC∽△A′B′C′
相似三角形的判定:
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
课前练习:
2. 在△ABC中,DE∥BC, 若AD:DB=1:3,
DE=2,则BC的长为( )
解:∵ DE∥BC
∴ △ADE∽△ABC
相似三角形的判定:
平行于三角形一边的直线与其它两边相交, 所构成的三角形与原三角形相似。
B
C
E
D
A
8
∴AD:AB=DE:BC
∵AD:DB=1:3
∴AD:AB=1:4
∵ DE=2
∴4:BC=1:4
∴BC=8 三角形ADE:三角形ABC=1:16
1:16
课前练习:
3.如图,等腰三角形ABC中,AB=AC,AD是高,BE是中线,AD、BE交于点F,BC=10,AF=8,
则AB= ( )
13
∵ 等腰三角形ABC中,AD是高,BE是中线
∴F是三角形ABC的重心
AF=2FD
∵AF=8
∴FD=4,即AD=12
∵AD⊥BC,2BD=2DC=BC
∴Rt △ABD中,AD=12,BD=5
∴由勾股定理,可得AB=13
相似三角形的判定
(1)平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似。
(2)如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
(3)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
(4)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
相似三角形的性质
(1)对应边的比相等,对应角相等
(2)相似三角形的周长比等于相似比
(3)相似三角形的面积比等于相似比的平方
(4)相似三角形的对应边上的高、中线、角平分线的比等于相似比
相似三角形的应用:
1. 利用三角形相似,可证明角相等;线 段成比例(或等积式)
2. 利用三角形相似,求线段的长等;
3. 利用三角形相似,可以解决一些不能直接测量的物体的长度。如求河的宽度、求建筑物的高度等。
课堂练习:
D是△ABC的边AB上的点, 请你添加一个条件,使△ACD与△ABC相似, 这个条件是( )
①∠ADC=∠ACB
② ∠ACD=∠B
③
如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为( )
A
D
C
B
15
课堂练习:
如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F,BE:AB=2:3,则△BEF与△CDF的周长比为( );若△BEF的面积为8平方厘米,则△CDF的面积为( )
2:3
18平方厘米
A
B
E
C
D
F
课堂练习:
如图,火焰AC通过纸板EF上的一个小孔O照射到屏幕上形成倒立的实像.像的长度BD=2cm,OA=60cm,OB=20cm,火焰AC的长是 cm.
解:由实际意义知:AC//BD,
∴ AC//BD
∴△ACO∽△OBD
∴AO:BO=AC:BD
∵AO=60m,BO=20m
∴60:20=AC:2
解得:AC=6(cm)
∴火焰长是6厘米。
6
课堂练习:
如图,阳光通过窗口照亮到室内,在地面上留下2.7m宽的亮区DE,已知亮区DE到窗口下的墙角距离EC=8.7m,窗口高AB=1.8m,那么窗口底边离地面的高BC= m
A. 4.8m B. 6.4m
C. 5.8m D. 10m
解:由实际意义知:AD//BE,
∵ AC//BD
∴CE:DE=CB:BA
∵CE=8.7m, DE=2.7m
BA=1.8m
∴8.7:2.7=CB:1.8
解得:BC=5.8(cm)
∴窗口离地面的高度BC是5.8m。
C
练一练
1. 如图,△ABD∽ △ACE
求证: △ABC ∽ △ADE
2.如图,在△ABC中,AB=AC,∠EDF=∠B,点D、E、F分别在BC、AB、AC上,
求证:BD×CD=BE×CF.
图(1)
拓展:
某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上种植花木(如图)他们想在△AMD和△BMC地带种植单价为10元 /米2的太阳花,当△AMD地带种满花后,已经花了500元,请你算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由。
拓展:
如图,在直角△ABC中,∠C=90°,AC=3㎝,BC=4㎝,设P、Q分别为AB上的动点,在点P自点A沿AB方向向点B做匀速移动的同时,点Q自点B沿BC方向向点C做匀速移动,他们移动的速度均为每秒1㎝,当点Q到达点C时,P点就停止运动。设P、Q移动的时间为t秒.
(1)写出△PBQ的面积S(cm2)与时间t(秒)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,△PBQ为等腰三角形?
(3)△PBQ能否与直角三角形ABC相似?若能,求t的值,若不能,说明理由
小结:
(1)掌握相似三角形的判定方法及性质;
(2)能灵活运用相似三角形的判定方法及性质进行计算或证明;
(3)利用相似解决一些实际问题
通这一节的复习之后你有哪些收获?
作业:
完成教学告白后的课后练习
