6.2角

(共19张PPT)
6.2 角的认识
教学目标:
★ 了解角的相关概念，掌握角的表示方法。
★ 能估计一个角的大小，会使用量角器量角的大小，认识度、分、秒，会进行简单换算。
★ 能写出角的和与差的关系式。
有三名运动员在不同的位置射门,
你觉得哪个位置射门进球的可能性
最大 哪个位置射门进球的可能性
最小
时钟的时针与分针组成的是什么图形？
3点
9点
5点
7点
谁能够准确说出在小学里，
学过的角的概念？
比一比
谁学的牢
角的概念：角是由两条具有公共端点
的射线组成的，两条射线的公共端点
是这个角的顶点，这两条射线是这个
角的边；角也可以看成有一条射线绕
着它的端点旋转而形成的．
A
B
C
D
E
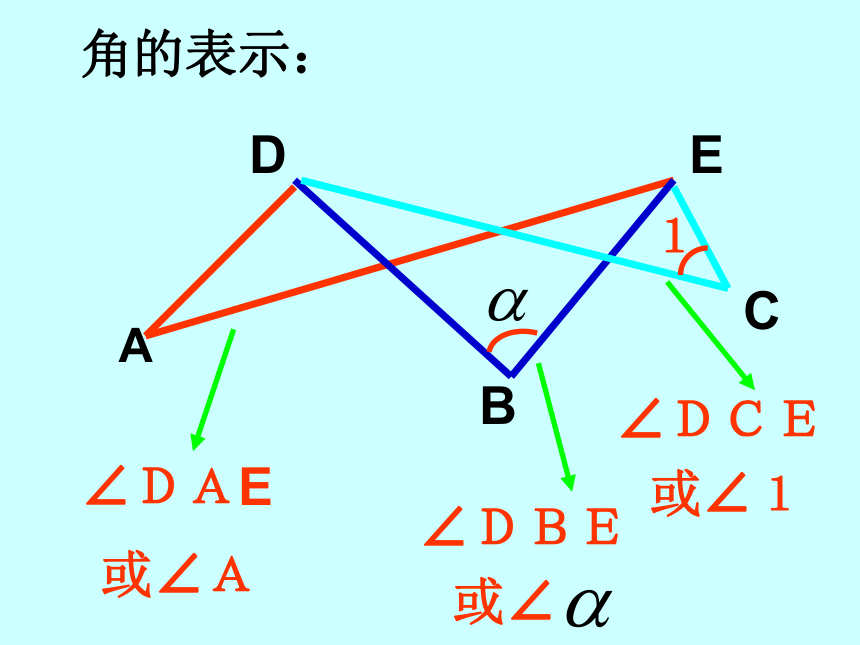
角的表示：
∠ＤＡE
∠ＤＢＥ
∠ＤＣＥ
或∠Ａ
或∠
１
或∠１
在角的表示时，应注意：
　　１、用３个字母来表示角时，表示
顶点的字母必须写在另两个字母的中间；
　　２、在不引起混淆时，角才可以用
的顶点字母来表示；
　　３、一般地，用一个数字或一个希
腊字母表示时，需在角内靠近顶点处画
上弧线。
已知，如图，C、D是OA上两点，
E、F是OB上两点，下列各式中，
表示∠AOB错误的是（ ）
A、 ∠COE B、 ∠AOF
C、 ∠DOB D、 ∠EOF
D
如图，将图中∠1、 ∠2、 ∠3表示的角
改用大写字母表示分别为___________
∠ADE
∠CED
∠ABC
∠B
如图，打台球时，球的反射角总是等于入射角。（见课本１５３页）
请估测图中入射角的度数，
估测球反弹后会撞击图中的哪一点？
Ｏ
Ａ
Ｂ
Ｃ
Ｄ
１、如图，以ＯＡ为一边的
角有哪几个？你能按从小到
大的顺序用“<”号连接起来吗？
∠ＡＯＤ
∠ＡＯＣ
∠ＡＯＢ
〈
〈
２、 ∠ＡＯＣ＝ ∠ＡＯＢ＋ ∠ＢＯＣ，
∠ＡＯＢ＝ ∠ＡＯＤ－ ∠ＤＯＢ，类似地，你还能写出哪些有关角的和与差？
我能！
（１）图中共有多少个角？
　　　用字母分别表示出来；
（２）图中各角之间有怎样的大小关系？
Ｏ
Ａ
Ｂ
Ｃ
Ａ
∠ＡＯＣ
∠ＢＯＣ
∠ＡＯＢ
〈
〈
∠ＡＯＣ＝∠ＡＯＢ＋ ∠ＢＯＣ
∠ＡＯＢ＝ ∠ＡＯＣ－ ∠ＢＯＣ
∠ＢＯＣ＝ ∠ＡＯＣ－ ∠ＡＯＢ
一、角的大小我们怎么表示呢？
我们常用量角器量角，度、分、秒是
常用的角的度量单位。
　二、度、分、秒之间关系：
１Ｏ的　　　为１分，记１/，即１Ｏ＝６０/
１/的　　　为１秒，记１//，即１/＝６０//
练一练
2、
1、抢答：
(1) 1o = ________//;
(2) 1 // = (________)/;
(3) 1/ = (________)o;
（4） 1// = (________)o;
　（5） 15/＝_______O＝______//;
　（6） 0.2Ｏ＝_______/＝______//。
　　
0.25
900
12
720
45
78.9
3600
1/60
1/60
1/3600
课堂小结
1、认识 并会表示角，知道角的度量单位：度、分、秒，会进行简单的换算；
2、会比较、估计角的大小，能根据图形写出
图中有关角的和与差的关系式。
O
A
B
C
Ｏ
Ａ
Ｂ
Ｃ
Ｄ
∠AOC＝ ∠AOB＋ ∠BOC，
∠AOB＝ ∠AOD－ ∠DOB
∠AOC＝ ∠AOD—∠COD，
∠AOD＝ ∠AOC + ∠COD
∠BOD＝ ∠COD＋ ∠BOC，
∠BOC＝ ∠BOD－ ∠COD
∠BOC＝ ∠AOC —∠AOB，
∠BOD＝ ∠AOD－ ∠AOB
∠COD＝ ∠AOD － ∠AOC，
∠AOB＝ ∠AOC－ ∠BOC
∠COD＝ ∠BOD － ∠BOC，
∠AOD＝ ∠AOB + ∠BOD
你真棒！