2020-2021学年黑龙江省哈尔滨市南岗区“NF联盟”八年级(上)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市南岗区“NF联盟”八年级(上)期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 826.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 05:29:37 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市南岗区“NF联盟”八年级第一学期期中数学试卷
一、选择题(共10小题).
1.(3分)如图图形中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
2.(3分)下列计算正确的是( )
A.a2+a2=a4 B.(a3)3=a6 C.a3×a3=a6 D.a2×a3=a6
3.(3分)点M(3,2)关于y轴对称的点的坐标为( )
A.(﹣3,2) B.(3,﹣2) C.(﹣3,﹣2) D.(3,2)
4.(3分)一个等腰三角形的顶角是50°,则它的底角是( )
A.100° B.65° C.70° D.75°
5.(3分)如图,已知△ABC中,AB=AC,BD=DC,则下列结论错误的是( )
A.∠BAC=∠B B.∠BAD=∠CAD C.AD⊥BC D.∠B=∠C
6.(3分)到三角形三个顶点距离相等的是( )
A.三边高线的交点 B.三条中线的交点
C.三条垂直平分线的交点 D.三条内角平分线的交点
7.(3分)如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=8,AD=5,则AB等于( )
A.12 B.13 C.14 D.15
8.(3分)如果x2+kx+6=(x+2)(x+3),则k=( )
A.1 B.2 C.3 D.5
9.(3分)如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
A.2 B.3 C.6 D.8
10.(3分)下列说法正确的有( )
①任何数的0次幂都得1;
②等腰三角形的高、中线、角平分线互相重合;
③有一个角是60°的三角形是等边三角形;
④若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;
⑤等腰三角形的对称轴是顶角的平分线.
A.1个 B.2个 C.3个 D.4个
二、填空题(共10小题).
11.(3分)计算:(2x)2= .
12.(3分)把多项式3ax2﹣12a分解因式的结果是 .
13.(3分)(8a3b﹣4a2b2)÷2ab= .
14.(3分)am=2,an=3,则am+n= .
15.(3分)等腰三角形的两边长为5cm、2cm,则此三角形的周长为 cm.
16.(3分)如图,DE是AB的垂直平分线,D是垂足,DE交BC于E,若BC=32cm,AC=18cm,则△AEC的周长为 cm.
17.(3分)如图,AB=AC,BD=CD,AD=AE,∠EDC=16°,则∠BAD= 度.
18.(3分)已知x2+y2=10,xy=4,求(x+y)2的值为 .
19.(3分)一个等腰三角形一腰上的高与另一腰的夹角为36°,则此三角形顶角度数为 .
20.(3分)如图,BH是钝角三角形ABC的高,AD是角平分线,且2∠C=90°﹣∠ABH,若CD=4,△ABC的面积为12,则AD= .
三、解答题(其中21-22题各7分,23-24题各分,25-27题各10分,共计60分)
21.(7分)计算:
(1)3a(a+b);
(2)(x﹣1)(x+4).
22.(7分)先化简,再求值:(x﹣3)2+(x+1)(x﹣1),其中x=2.
23.(8分)按要求完成作图:
(1)作△ABC关于y轴对称的△A1B1C1;
(2)直接写出点A1的坐标 .
(3)直接写出△ABC的面积 .
24.(8分)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
25.(10分)如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2,请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系: ;
(3)根据(2)题中的等量关系,解决下面的问题:已知a+b=3,ab=2,求a3b﹣ab3的值.
26.(10分)已知,在等边△ABC中,D、E分别为AC、BC边上的点,BE=CD,连接AE、BD相交于点F.
(1)如图1,求∠AFD的度数;
(2)如图2,过点A作AH⊥BD于H,若EF=HD,求证:BF=HF;
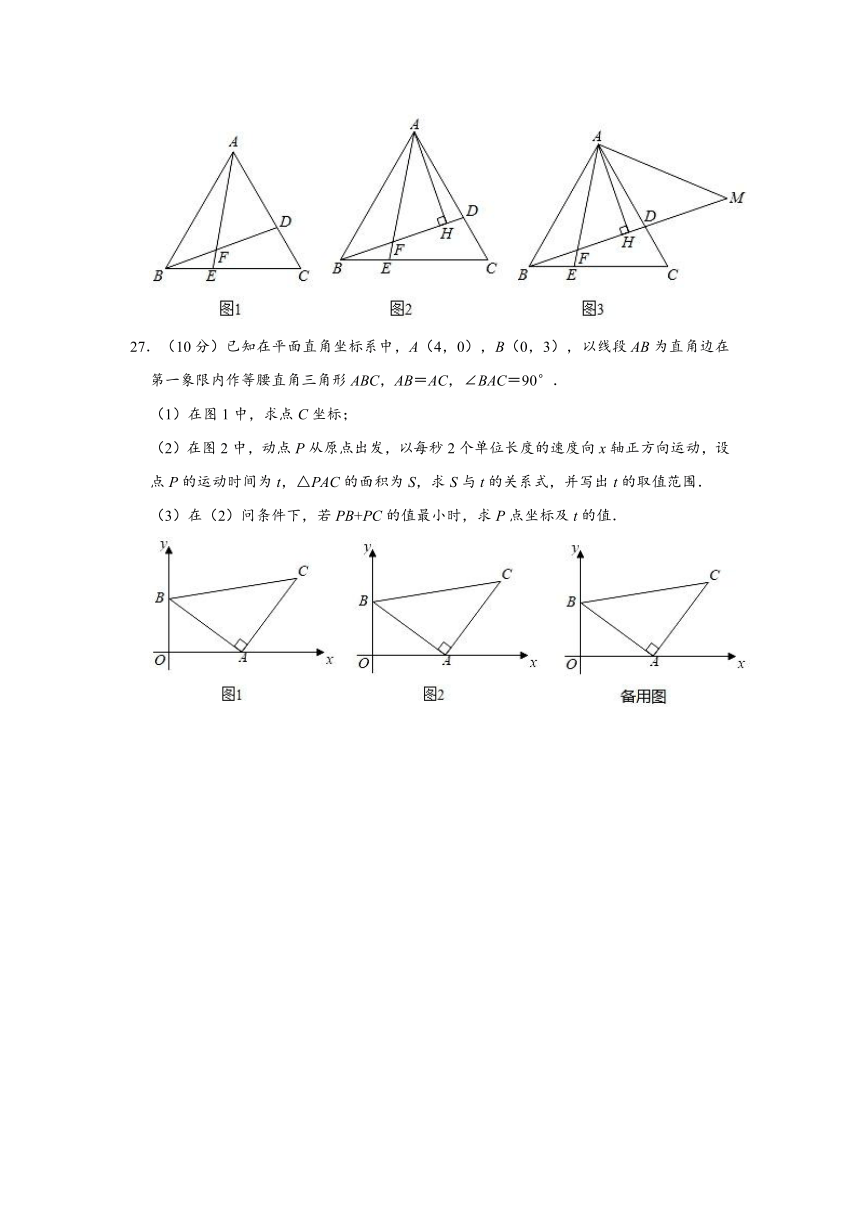
(3)如图3,在(2)的条件下,延长BD到点M,连接AM,使∠AMB=∠ABM,若EF=2,AF=10,求DM长.
27.(10分)已知在平面直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰直角三角形ABC,AB=AC,∠BAC=90°.
(1)在图1中,求点C坐标;
(2)在图2中,动点P从原点出发,以每秒2个单位长度的速度向x轴正方向运动,设点P的运动时间为t,△PAC的面积为S,求S与t的关系式,并写出t的取值范围.
(3)在(2)问条件下,若PB+PC的值最小时,求P点坐标及t的值.
参考答案
一、选择题(每小题3分,共计30分)
1.(3分)如图图形中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
解:第1个图形,不是轴对称图形,故本选项不合题意;
第2个图形,是轴对称图形,故本选项符合题意;
第3个图形,不是轴对称图形,故本选项不合题意;
第4个图形,是轴对称图形,故本选项符合题意.
故选:B.
2.(3分)下列计算正确的是( )
A.a2+a2=a4 B.(a3)3=a6 C.a3×a3=a6 D.a2×a3=a6
解:A、a2+a2=2a2,故本选项不合题意;
B、(a3)3=a9,故本选项不合题意;
C、a3×a3=a6 ,故本选项符合题意;
D、a2×a3=a5,故本选项不合题意;
故选:C.
3.(3分)点M(3,2)关于y轴对称的点的坐标为( )
A.(﹣3,2) B.(3,﹣2) C.(﹣3,﹣2) D.(3,2)
解:点M(3,2)关于y轴对称的点的坐标为(﹣3,2).
故选:A.
4.(3分)一个等腰三角形的顶角是50°,则它的底角是( )
A.100° B.65° C.70° D.75°
解:∵三角形为等腰三角形,且顶角为50°,
∴底角=(180°﹣50°)÷2=65°.
故选:B.
5.(3分)如图,已知△ABC中,AB=AC,BD=DC,则下列结论错误的是( )
A.∠BAC=∠B B.∠BAD=∠CAD C.AD⊥BC D.∠B=∠C
解:∵AB=AC,BD=DC,AD=AD,
∴△ADB≌△ADC(SSS),
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC,
故B,C,D正确,
故选:A.
6.(3分)到三角形三个顶点距离相等的是( )
A.三边高线的交点 B.三条中线的交点
C.三条垂直平分线的交点 D.三条内角平分线的交点
解:到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点,理由是:
∵P在AB的垂直平分线EF上,
∴PA=PB,
∵P在AC的垂直平分线MN上,
∴PA=PC,
∴PA=PC=PB,
即P是到三角形三个顶点的距离相等的点.
故选:C.
7.(3分)如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=8,AD=5,则AB等于( )
A.12 B.13 C.14 D.15
解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE=8,
∵AB=AD+BD,
∴AB=5+8=13.
故选:B.
8.(3分)如果x2+kx+6=(x+2)(x+3),则k=( )
A.1 B.2 C.3 D.5
解:由题意得,x2+kx+6=(x+2)(x+3)=x2+5x+6,
则可得k=5.
故选:D.
9.(3分)如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
A.2 B.3 C.6 D.8
解:∵在△ABC中,∠C=90°,∠A=30°,
∴BC=AB=×6=3,
故选:B.
10.(3分)下列说法正确的有( )
①任何数的0次幂都得1;
②等腰三角形的高、中线、角平分线互相重合;
③有一个角是60°的三角形是等边三角形;
④若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;
⑤等腰三角形的对称轴是顶角的平分线.
A.1个 B.2个 C.3个 D.4个
解:①任何数的0次幂都得1,错误,0的0次幂没有意义.
②等腰三角形的高、中线、角平分线互相重合,错误,应该是等腰三角形的底边上的高、中线、顶角的角平分线互相重合.
③有一个角是60°的三角形是等边三角形,错误,应该是有一个角是60°的等腰三角形是等边三角形.
④若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等,正确.
⑤等腰三角形的对称轴是顶角的平分线,错误,应该是等腰三角形的对称轴是顶角的平分线所在的直线.
故选:A.
二、填空题(每小题3分,共计30分)
11.(3分)计算:(2x)2= 4x2 .
解:(2x)2=4x2.
故答案为:4x2.
12.(3分)把多项式3ax2﹣12a分解因式的结果是 3a(x+2)(x﹣2) .
解:3ax2﹣12a=3a(x2﹣4)=3a(x+2)(x﹣2),
故答案为:3a(x+2)(x﹣2).
13.(3分)(8a3b﹣4a2b2)÷2ab= 4a2﹣2ab .
解:(8a3b﹣4a2b2)÷2ab
=8a3b÷2ab﹣4a2b2÷2ab
=4a2﹣2ab.
故答案为:4a2﹣2ab.
14.(3分)am=2,an=3,则am+n= 6 .
解:∵am=2,an=3,
∴am?an=am+n=2×3=6.
故答案为:6.
15.(3分)等腰三角形的两边长为5cm、2cm,则此三角形的周长为 12 cm.
解:①5cm为腰,2cm为底,此时周长为12cm;
②5cm为底,2cm为腰,则两边和小于第三边无法构成三角形,故舍去.
所以其周长是12cm.
故答案为:12.
16.(3分)如图,DE是AB的垂直平分线,D是垂足,DE交BC于E,若BC=32cm,AC=18cm,则△AEC的周长为 50 cm.
解:∵DE是AB的垂直平分线,
∴AE=BE.
∴△AEC的周长=AC+CE+AE=AC+BC=18+32=50(cm).
故填50.
17.(3分)如图,AB=AC,BD=CD,AD=AE,∠EDC=16°,则∠BAD= 32 度.
解:在△ABD和△ACD中,,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠ADB=∠ADC=90°,
∴∠ADE=90°﹣∠EDC=90°﹣16°=74°,
∵AD=AE,
∴∠AED=∠ADE=74°,
∴∠BAD=∠CAD=180°﹣2×74°=32°;
故答案为:32.
18.(3分)已知x2+y2=10,xy=4,求(x+y)2的值为 18 .
解:因为x2+y2=10,xy=4,
所以(x+y)2=x2+2xy+y2=x2+y2+2xy=10+2×4=18.
故答案为:18.
19.(3分)一个等腰三角形一腰上的高与另一腰的夹角为36°,则此三角形顶角度数为 54°或126° .
解:当△ABC是锐角三角形时,
∠ACD=36°,∠ADC=90°,
∴∠A=54°,
当△ABC是钝角三角形时,
∴∠ACD=36°,∠ADC=90°,
∴∠BAC=∠ADC+∠ACD=126°
故答案为:54°或126°
20.(3分)如图,BH是钝角三角形ABC的高,AD是角平分线,且2∠C=90°﹣∠ABH,若CD=4,△ABC的面积为12,则AD= 3 .
解:∵BH为△ABC的高,
∴∠AHB=90°,
∴∠BAH=90°﹣∠ABH,
而2∠C=90°﹣∠ABH,
∴∠BAH=2∠C,
∵∠BAH=∠C+∠ABC,
∴∠ABC=∠C,
∴△ABC为等腰三角形,
∵AD是角平分线,
∴AD⊥BC,BD=CD=4,
∵△ABC的面积为12,
∴×AD×BC=12,即×AD×8=12,
∴AD=3.
故答案为3.
三、解答题(其中21-22题各7分,23-24题各分,25-27题各10分,共计60分)
21.(7分)计算:
(1)3a(a+b);
(2)(x﹣1)(x+4).
解:(1)原式=3a2+3ab;
(2)原式=x2+4x﹣x﹣4=x2+3x﹣4.
22.(7分)先化简,再求值:(x﹣3)2+(x+1)(x﹣1),其中x=2.
解:原式=x2﹣6x+9+x2﹣1
=2x2﹣6x+8,
当x=2时,原式=2×4﹣12+8
=4.
23.(8分)按要求完成作图:
(1)作△ABC关于y轴对称的△A1B1C1;
(2)直接写出点A1的坐标 (4,1) .
(3)直接写出△ABC的面积 .
解:(1)如图所示,△A1B1C1即为所求;
(2)点A1的坐标为(4,1),
故答案为:(4,1);
(3)△ABC的面积=2×3﹣﹣﹣=,
故答案为:.
24.(8分)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
【解答】证明:(1)过点A作AF⊥BC于点F,
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BF=CF,
∴AB=AC.
(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,
∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,
25.(10分)如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: (m﹣n)2 ;
方法2: (m+n)2﹣4mn ;
(2)观察图2,请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系: (m+n)2﹣4mn=(m﹣n)2 ;
(3)根据(2)题中的等量关系,解决下面的问题:已知a+b=3,ab=2,求a3b﹣ab3的值.
解:(1)方法1:由图可得小正方形的边长为m﹣n,则阴影部分的面积为(m﹣n)2;
故答案为:(m﹣n)2;
方法2:阴影部分=(m+n)2﹣4mn,
故答案为:(m+n)2﹣4mn;
(2)由阴影部分的面积的两种不同算法,可得等式(m+n)2﹣4mn=(m﹣n)2;
(3)∵a+b=3,ab=2,
∴(a﹣b)2=(a+b)2﹣4ab=9﹣8=1,
∴a﹣b=±1,
∵a3b﹣ab3=ab(a2﹣b2)=ab(a﹣b)(a+b)
∴a3b﹣ab3=±6
26.(10分)已知,在等边△ABC中,D、E分别为AC、BC边上的点,BE=CD,连接AE、BD相交于点F.
(1)如图1,求∠AFD的度数;
(2)如图2,过点A作AH⊥BD于H,若EF=HD,求证:BF=HF;
(3)如图3,在(2)的条件下,延长BD到点M,连接AM,使∠AMB=∠ABM,若EF=2,AF=10,求DM长.
【解答】(1)解:∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∴∠AFD=∠ABF+∠BAF=∠ABF+∠CBD=∠ABC=60°.
(2)证明:由(1)得:△ABE≌△BCD,
∴∠BAE=∠CBD,AE=BD,
∴∠AFH=∠BAE+∠ABF=∠CBD+∠ABF=∠ABC=60°,
∵AH⊥BD,
∴∠FAH=30°,
∴HF=AF,
∵EF=HD,
∴AF=BH,
∴HF=BH,
∴BF=HF;
(3)解:由(2)得:BH=AF=10,HF=AF=5,BD=AE=AF+EF=12,
∵∠AMB=∠ABM,
∴AB=AM,
∵AH⊥BD,
∴MH=BH=10,
∴BM=2BH=20,
∴DM=BM﹣BD=20﹣12=8.
27.(10分)已知在平面直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰直角三角形ABC,AB=AC,∠BAC=90°.
(1)在图1中,求点C坐标;
(2)在图2中,动点P从原点出发,以每秒2个单位长度的速度向x轴正方向运动,设点P的运动时间为t,△PAC的面积为S,求S与t的关系式,并写出t的取值范围.
(3)在(2)问条件下,若PB+PC的值最小时,求P点坐标及t的值.
【解答】(1)解:过点C作CH⊥x轴于点H,如图1,
则∠AHC=90°.
∴∠AOB=∠BAC=∠AHC=90°,
∴∠OAB=180°﹣90°﹣∠HAC=90°﹣∠HAC=∠HCA.
在△AOB和△CHA中,
,
∴△AOB≌△CHA(AAS),
∴AO=CH=4,OB=HA=3,
∴OH=OA+AH=7,
∴点C的坐标为(7,4);
(2)当0≤t<2时,点P在点A的左侧,
∴PA=4﹣2t,
∴S△PAC===8﹣4t.
当t>2时,点P在点A的右侧,
∴PA=2t﹣4,
∴S△PAC==×4=4t﹣8.
综合以上可得S与t的关系式为;
(3)作点B关于x轴的对称点E,连接EC交x轴于点P,则PB+PC的值最小,
过点E作y轴的垂线,过点C作x轴的垂线,交于点F,
∵B(0,3),
∴E(0,﹣3),
∵C(7,4),
∴CF=4+3=7,
∴EF=CF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴∠OEP=45°,
∵∠EOP=90°,
∴∠OEP=∠OPE,
∴OE=OP=3,
∴P(3,0),t=.
一、选择题(共10小题).
1.(3分)如图图形中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
2.(3分)下列计算正确的是( )
A.a2+a2=a4 B.(a3)3=a6 C.a3×a3=a6 D.a2×a3=a6
3.(3分)点M(3,2)关于y轴对称的点的坐标为( )
A.(﹣3,2) B.(3,﹣2) C.(﹣3,﹣2) D.(3,2)
4.(3分)一个等腰三角形的顶角是50°,则它的底角是( )
A.100° B.65° C.70° D.75°
5.(3分)如图,已知△ABC中,AB=AC,BD=DC,则下列结论错误的是( )
A.∠BAC=∠B B.∠BAD=∠CAD C.AD⊥BC D.∠B=∠C
6.(3分)到三角形三个顶点距离相等的是( )
A.三边高线的交点 B.三条中线的交点
C.三条垂直平分线的交点 D.三条内角平分线的交点
7.(3分)如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=8,AD=5,则AB等于( )
A.12 B.13 C.14 D.15
8.(3分)如果x2+kx+6=(x+2)(x+3),则k=( )
A.1 B.2 C.3 D.5
9.(3分)如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
A.2 B.3 C.6 D.8
10.(3分)下列说法正确的有( )
①任何数的0次幂都得1;
②等腰三角形的高、中线、角平分线互相重合;
③有一个角是60°的三角形是等边三角形;
④若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;
⑤等腰三角形的对称轴是顶角的平分线.
A.1个 B.2个 C.3个 D.4个
二、填空题(共10小题).
11.(3分)计算:(2x)2= .
12.(3分)把多项式3ax2﹣12a分解因式的结果是 .
13.(3分)(8a3b﹣4a2b2)÷2ab= .
14.(3分)am=2,an=3,则am+n= .
15.(3分)等腰三角形的两边长为5cm、2cm,则此三角形的周长为 cm.
16.(3分)如图,DE是AB的垂直平分线,D是垂足,DE交BC于E,若BC=32cm,AC=18cm,则△AEC的周长为 cm.
17.(3分)如图,AB=AC,BD=CD,AD=AE,∠EDC=16°,则∠BAD= 度.
18.(3分)已知x2+y2=10,xy=4,求(x+y)2的值为 .
19.(3分)一个等腰三角形一腰上的高与另一腰的夹角为36°,则此三角形顶角度数为 .
20.(3分)如图,BH是钝角三角形ABC的高,AD是角平分线,且2∠C=90°﹣∠ABH,若CD=4,△ABC的面积为12,则AD= .
三、解答题(其中21-22题各7分,23-24题各分,25-27题各10分,共计60分)
21.(7分)计算:
(1)3a(a+b);
(2)(x﹣1)(x+4).
22.(7分)先化简,再求值:(x﹣3)2+(x+1)(x﹣1),其中x=2.
23.(8分)按要求完成作图:
(1)作△ABC关于y轴对称的△A1B1C1;
(2)直接写出点A1的坐标 .
(3)直接写出△ABC的面积 .
24.(8分)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
25.(10分)如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2,请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系: ;
(3)根据(2)题中的等量关系,解决下面的问题:已知a+b=3,ab=2,求a3b﹣ab3的值.
26.(10分)已知,在等边△ABC中,D、E分别为AC、BC边上的点,BE=CD,连接AE、BD相交于点F.
(1)如图1,求∠AFD的度数;
(2)如图2,过点A作AH⊥BD于H,若EF=HD,求证:BF=HF;
(3)如图3,在(2)的条件下,延长BD到点M,连接AM,使∠AMB=∠ABM,若EF=2,AF=10,求DM长.
27.(10分)已知在平面直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰直角三角形ABC,AB=AC,∠BAC=90°.
(1)在图1中,求点C坐标;
(2)在图2中,动点P从原点出发,以每秒2个单位长度的速度向x轴正方向运动,设点P的运动时间为t,△PAC的面积为S,求S与t的关系式,并写出t的取值范围.
(3)在(2)问条件下,若PB+PC的值最小时,求P点坐标及t的值.
参考答案
一、选择题(每小题3分,共计30分)
1.(3分)如图图形中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
解:第1个图形,不是轴对称图形,故本选项不合题意;
第2个图形,是轴对称图形,故本选项符合题意;
第3个图形,不是轴对称图形,故本选项不合题意;
第4个图形,是轴对称图形,故本选项符合题意.
故选:B.
2.(3分)下列计算正确的是( )
A.a2+a2=a4 B.(a3)3=a6 C.a3×a3=a6 D.a2×a3=a6
解:A、a2+a2=2a2,故本选项不合题意;
B、(a3)3=a9,故本选项不合题意;
C、a3×a3=a6 ,故本选项符合题意;
D、a2×a3=a5,故本选项不合题意;
故选:C.
3.(3分)点M(3,2)关于y轴对称的点的坐标为( )
A.(﹣3,2) B.(3,﹣2) C.(﹣3,﹣2) D.(3,2)
解:点M(3,2)关于y轴对称的点的坐标为(﹣3,2).
故选:A.
4.(3分)一个等腰三角形的顶角是50°,则它的底角是( )
A.100° B.65° C.70° D.75°
解:∵三角形为等腰三角形,且顶角为50°,
∴底角=(180°﹣50°)÷2=65°.
故选:B.
5.(3分)如图,已知△ABC中,AB=AC,BD=DC,则下列结论错误的是( )
A.∠BAC=∠B B.∠BAD=∠CAD C.AD⊥BC D.∠B=∠C
解:∵AB=AC,BD=DC,AD=AD,
∴△ADB≌△ADC(SSS),
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC,
故B,C,D正确,
故选:A.
6.(3分)到三角形三个顶点距离相等的是( )
A.三边高线的交点 B.三条中线的交点
C.三条垂直平分线的交点 D.三条内角平分线的交点
解:到三角形三个顶点的距离相等的点是三角形三边垂直平分线的交点,理由是:
∵P在AB的垂直平分线EF上,
∴PA=PB,
∵P在AC的垂直平分线MN上,
∴PA=PC,
∴PA=PC=PB,
即P是到三角形三个顶点的距离相等的点.
故选:C.
7.(3分)如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=8,AD=5,则AB等于( )
A.12 B.13 C.14 D.15
解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE=8,
∵AB=AD+BD,
∴AB=5+8=13.
故选:B.
8.(3分)如果x2+kx+6=(x+2)(x+3),则k=( )
A.1 B.2 C.3 D.5
解:由题意得,x2+kx+6=(x+2)(x+3)=x2+5x+6,
则可得k=5.
故选:D.
9.(3分)如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
A.2 B.3 C.6 D.8
解:∵在△ABC中,∠C=90°,∠A=30°,
∴BC=AB=×6=3,
故选:B.
10.(3分)下列说法正确的有( )
①任何数的0次幂都得1;
②等腰三角形的高、中线、角平分线互相重合;
③有一个角是60°的三角形是等边三角形;
④若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等;
⑤等腰三角形的对称轴是顶角的平分线.
A.1个 B.2个 C.3个 D.4个
解:①任何数的0次幂都得1,错误,0的0次幂没有意义.
②等腰三角形的高、中线、角平分线互相重合,错误,应该是等腰三角形的底边上的高、中线、顶角的角平分线互相重合.
③有一个角是60°的三角形是等边三角形,错误,应该是有一个角是60°的等腰三角形是等边三角形.
④若△ABC与△DEF成轴对称,则△ABC一定与△DEF全等,正确.
⑤等腰三角形的对称轴是顶角的平分线,错误,应该是等腰三角形的对称轴是顶角的平分线所在的直线.
故选:A.
二、填空题(每小题3分,共计30分)
11.(3分)计算:(2x)2= 4x2 .
解:(2x)2=4x2.
故答案为:4x2.
12.(3分)把多项式3ax2﹣12a分解因式的结果是 3a(x+2)(x﹣2) .
解:3ax2﹣12a=3a(x2﹣4)=3a(x+2)(x﹣2),
故答案为:3a(x+2)(x﹣2).
13.(3分)(8a3b﹣4a2b2)÷2ab= 4a2﹣2ab .
解:(8a3b﹣4a2b2)÷2ab
=8a3b÷2ab﹣4a2b2÷2ab
=4a2﹣2ab.
故答案为:4a2﹣2ab.
14.(3分)am=2,an=3,则am+n= 6 .
解:∵am=2,an=3,
∴am?an=am+n=2×3=6.
故答案为:6.
15.(3分)等腰三角形的两边长为5cm、2cm,则此三角形的周长为 12 cm.
解:①5cm为腰,2cm为底,此时周长为12cm;
②5cm为底,2cm为腰,则两边和小于第三边无法构成三角形,故舍去.
所以其周长是12cm.
故答案为:12.
16.(3分)如图,DE是AB的垂直平分线,D是垂足,DE交BC于E,若BC=32cm,AC=18cm,则△AEC的周长为 50 cm.
解:∵DE是AB的垂直平分线,
∴AE=BE.
∴△AEC的周长=AC+CE+AE=AC+BC=18+32=50(cm).
故填50.
17.(3分)如图,AB=AC,BD=CD,AD=AE,∠EDC=16°,则∠BAD= 32 度.
解:在△ABD和△ACD中,,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠ADB=∠ADC=90°,
∴∠ADE=90°﹣∠EDC=90°﹣16°=74°,
∵AD=AE,
∴∠AED=∠ADE=74°,
∴∠BAD=∠CAD=180°﹣2×74°=32°;
故答案为:32.
18.(3分)已知x2+y2=10,xy=4,求(x+y)2的值为 18 .
解:因为x2+y2=10,xy=4,
所以(x+y)2=x2+2xy+y2=x2+y2+2xy=10+2×4=18.
故答案为:18.
19.(3分)一个等腰三角形一腰上的高与另一腰的夹角为36°,则此三角形顶角度数为 54°或126° .
解:当△ABC是锐角三角形时,
∠ACD=36°,∠ADC=90°,
∴∠A=54°,
当△ABC是钝角三角形时,
∴∠ACD=36°,∠ADC=90°,
∴∠BAC=∠ADC+∠ACD=126°
故答案为:54°或126°
20.(3分)如图,BH是钝角三角形ABC的高,AD是角平分线,且2∠C=90°﹣∠ABH,若CD=4,△ABC的面积为12,则AD= 3 .
解:∵BH为△ABC的高,
∴∠AHB=90°,
∴∠BAH=90°﹣∠ABH,
而2∠C=90°﹣∠ABH,
∴∠BAH=2∠C,
∵∠BAH=∠C+∠ABC,
∴∠ABC=∠C,
∴△ABC为等腰三角形,
∵AD是角平分线,
∴AD⊥BC,BD=CD=4,
∵△ABC的面积为12,
∴×AD×BC=12,即×AD×8=12,
∴AD=3.
故答案为3.
三、解答题(其中21-22题各7分,23-24题各分,25-27题各10分,共计60分)
21.(7分)计算:
(1)3a(a+b);
(2)(x﹣1)(x+4).
解:(1)原式=3a2+3ab;
(2)原式=x2+4x﹣x﹣4=x2+3x﹣4.
22.(7分)先化简,再求值:(x﹣3)2+(x+1)(x﹣1),其中x=2.
解:原式=x2﹣6x+9+x2﹣1
=2x2﹣6x+8,
当x=2时,原式=2×4﹣12+8
=4.
23.(8分)按要求完成作图:
(1)作△ABC关于y轴对称的△A1B1C1;
(2)直接写出点A1的坐标 (4,1) .
(3)直接写出△ABC的面积 .
解:(1)如图所示,△A1B1C1即为所求;
(2)点A1的坐标为(4,1),
故答案为:(4,1);
(3)△ABC的面积=2×3﹣﹣﹣=,
故答案为:.
24.(8分)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.
(1)求证:AB=AC;
(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.
【解答】证明:(1)过点A作AF⊥BC于点F,
∵AD=AE,
∴DF=EF,
∵BD=CE,
∴BF=CF,
∴AB=AC.
(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,
∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,
25.(10分)如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: (m﹣n)2 ;
方法2: (m+n)2﹣4mn ;
(2)观察图2,请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系: (m+n)2﹣4mn=(m﹣n)2 ;
(3)根据(2)题中的等量关系,解决下面的问题:已知a+b=3,ab=2,求a3b﹣ab3的值.
解:(1)方法1:由图可得小正方形的边长为m﹣n,则阴影部分的面积为(m﹣n)2;
故答案为:(m﹣n)2;
方法2:阴影部分=(m+n)2﹣4mn,
故答案为:(m+n)2﹣4mn;
(2)由阴影部分的面积的两种不同算法,可得等式(m+n)2﹣4mn=(m﹣n)2;
(3)∵a+b=3,ab=2,
∴(a﹣b)2=(a+b)2﹣4ab=9﹣8=1,
∴a﹣b=±1,
∵a3b﹣ab3=ab(a2﹣b2)=ab(a﹣b)(a+b)
∴a3b﹣ab3=±6
26.(10分)已知,在等边△ABC中,D、E分别为AC、BC边上的点,BE=CD,连接AE、BD相交于点F.
(1)如图1,求∠AFD的度数;
(2)如图2,过点A作AH⊥BD于H,若EF=HD,求证:BF=HF;
(3)如图3,在(2)的条件下,延长BD到点M,连接AM,使∠AMB=∠ABM,若EF=2,AF=10,求DM长.
【解答】(1)解:∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∴∠AFD=∠ABF+∠BAF=∠ABF+∠CBD=∠ABC=60°.
(2)证明:由(1)得:△ABE≌△BCD,
∴∠BAE=∠CBD,AE=BD,
∴∠AFH=∠BAE+∠ABF=∠CBD+∠ABF=∠ABC=60°,
∵AH⊥BD,
∴∠FAH=30°,
∴HF=AF,
∵EF=HD,
∴AF=BH,
∴HF=BH,
∴BF=HF;
(3)解:由(2)得:BH=AF=10,HF=AF=5,BD=AE=AF+EF=12,
∵∠AMB=∠ABM,
∴AB=AM,
∵AH⊥BD,
∴MH=BH=10,
∴BM=2BH=20,
∴DM=BM﹣BD=20﹣12=8.
27.(10分)已知在平面直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰直角三角形ABC,AB=AC,∠BAC=90°.
(1)在图1中,求点C坐标;
(2)在图2中,动点P从原点出发,以每秒2个单位长度的速度向x轴正方向运动,设点P的运动时间为t,△PAC的面积为S,求S与t的关系式,并写出t的取值范围.
(3)在(2)问条件下,若PB+PC的值最小时,求P点坐标及t的值.
【解答】(1)解:过点C作CH⊥x轴于点H,如图1,
则∠AHC=90°.
∴∠AOB=∠BAC=∠AHC=90°,
∴∠OAB=180°﹣90°﹣∠HAC=90°﹣∠HAC=∠HCA.
在△AOB和△CHA中,
,
∴△AOB≌△CHA(AAS),
∴AO=CH=4,OB=HA=3,
∴OH=OA+AH=7,
∴点C的坐标为(7,4);
(2)当0≤t<2时,点P在点A的左侧,
∴PA=4﹣2t,
∴S△PAC===8﹣4t.
当t>2时,点P在点A的右侧,
∴PA=2t﹣4,
∴S△PAC==×4=4t﹣8.
综合以上可得S与t的关系式为;
(3)作点B关于x轴的对称点E,连接EC交x轴于点P,则PB+PC的值最小,
过点E作y轴的垂线,过点C作x轴的垂线,交于点F,
∵B(0,3),
∴E(0,﹣3),
∵C(7,4),
∴CF=4+3=7,
∴EF=CF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴∠OEP=45°,
∵∠EOP=90°,
∴∠OEP=∠OPE,
∴OE=OP=3,
∴P(3,0),t=.
同课章节目录
