20.4 函数的初步应用 课件(19张PPT)
文档属性
| 名称 | 20.4 函数的初步应用 课件(19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 781.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 10:43:47 | ||
图片预览





文档简介
导入新课
讲授新课
当堂练习
课堂小结
20.4 函数的初步应用
第二十章 函数
学习目标
1.能够从函数的各种表示方法中获得相应的信息,运用函数解决简单的实际问题.(重点、难点)
2.体会函数模型的作用,增强数学应用意识.
导入新课
情境引入
常用的温度计量标准有两种,一种是摄氏温度(℃),另一种是华氏温度(℉).
想一想:华氏温度与摄氏温度是否具有函数关系呢?
讲授新课
确定实际问题中的函数关系式
一
已知摄氏温度值和华氏温度值有下表所示的对应关系:
摄氏温度/?C
0
10
20
30
40
50
华氏温度/?F
32
50
68
86
104
122
(1)当摄氏温度为30时,华氏温度为多少?
合作探究
86
摄氏温度/?C
0
10
20
30
40
50
华氏温度/?F
32
50
68
86
104
122
(2)当摄氏温度为36时,由数值表能直接看出华氏温度吗?试写出这两种温度计量之间关系的函数表达式,并求摄氏温度为36时的华氏温度;
(3)当华氏温度为140时,摄氏温度为多少?
若设摄氏温度为S ?C,华氏温度为H ?F,则
H=1.8S+32.
当S=36时,H=96.8
因为H=1.8S+32=140,所以S=60.
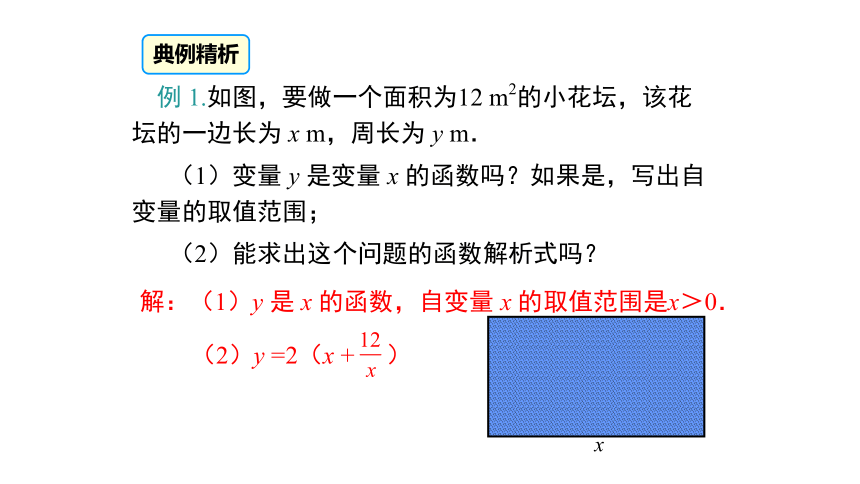
例 1.如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
x
解:(1)y 是 x 的函数,自变量 x 的取值范围是x>0.
(2)y =2(x + )
典例精析
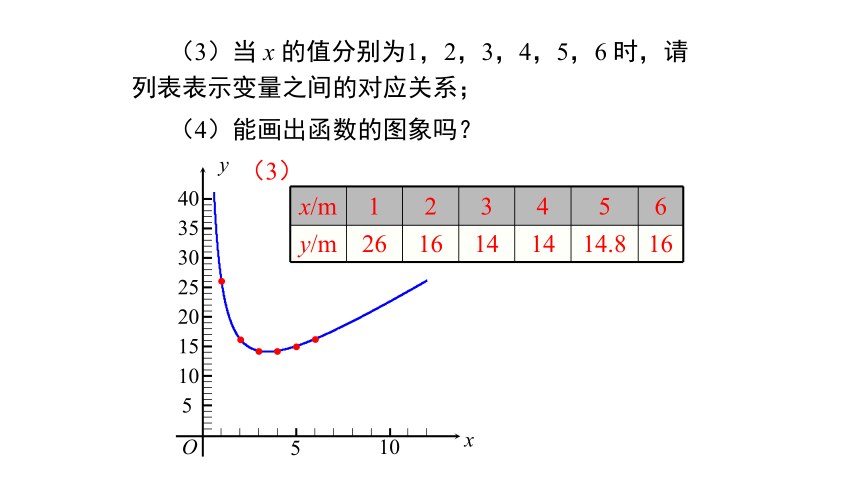
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出函数的图象吗?
x/m
1
2
3
4
5
6
y/m
26
16
14
14
14.8
16
40
35
30
25
20
15
10
5
5
10
O
x
y
(3)
已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少cm?
解:
x>0
(2)当x=10时,y=60÷10=6
x
y
60
=
(1)
做一做
例2 一个游泳池内有水300 m3,现打开排水管以每小时25 m3的排出量排水.
(1)写出游泳池内剩余水量Q m3与排水时间th间的函数关系式;
(2)写出自变量t的取值范围.
排水后的剩水量Q m3是排水时间h的函
数,有Q=-25 t +300.
池中共有300 m3水,每小时排水25 m3,故全部排完只需 300÷25=12(h),故自变量 t的取值范围是0≤t≤12.
(3)开始排水后的第5h末,游泳池中还有多少水?
(4)当游泳池中还剩150 m3水时,已经排水多长时间?
当t=5,代入上式得Q=-5×25+300=175(m3),
即第5h末池中还有水175 m3
当Q=150m3时,由150=-25 t +300,得t =6h,
即第6 h末池中有水150m3.
【归纳】实际问题中自变量的取值范围.
在实际问题中确定自变量的取值范围,主
要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
例 3.一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,
这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每
小时水位 .由此猜想,在这个时间
段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
5
(2)水位高度 y 是否为时间 t 的函数?如果是,试写
出一个符合表中数据的函数解析式,并画出函数图象.
这个函数能表示水位的变化规律吗?
(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: .
自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
(3)如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
已知火车站托运行李的费用C(元)和托运行李的重量P(千克)(P为整数)的对应关系如表:
做一做
P
1
2
3
4
5
…
C
2
2.5
3
3.5
4
…
(1)已知小周的所要托运的行李重12千克,请问小周托运行李的费用为多少元?
(2)写出C与P之间的函数解析式.
(3)小李托运行李花了15元钱,请问小李的行李重多少千克?
7.5元
C=0.5P+1.5
27千克
1.用列表法与表达式法表示n边形的内角和m(单位:度)是边数n的函数.
解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下:
n
3
4
5
6
…
m
…
所以m=(n-2)·180°(n≥3,且n为自然数).
180
360
540
720
提示:n边形的内角和公式是:(n-2) ×180°.
当堂练习
2.用表达式法与图象法表示等边三角形的周长l是边长a的函数.
a
…
1
2
3
4
…
l
…
3
6
9
12
…
描点、连线:
用描点法画函数l=3a的图象.
O
2
x
y
1
2
3
4
5
8
6
4
10
12
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).
课堂小结
函数的初步应用
确定实际问题中函数关系式
描实际问题中的函数图像
讲授新课
当堂练习
课堂小结
20.4 函数的初步应用
第二十章 函数
学习目标
1.能够从函数的各种表示方法中获得相应的信息,运用函数解决简单的实际问题.(重点、难点)
2.体会函数模型的作用,增强数学应用意识.
导入新课
情境引入
常用的温度计量标准有两种,一种是摄氏温度(℃),另一种是华氏温度(℉).
想一想:华氏温度与摄氏温度是否具有函数关系呢?
讲授新课
确定实际问题中的函数关系式
一
已知摄氏温度值和华氏温度值有下表所示的对应关系:
摄氏温度/?C
0
10
20
30
40
50
华氏温度/?F
32
50
68
86
104
122
(1)当摄氏温度为30时,华氏温度为多少?
合作探究
86
摄氏温度/?C
0
10
20
30
40
50
华氏温度/?F
32
50
68
86
104
122
(2)当摄氏温度为36时,由数值表能直接看出华氏温度吗?试写出这两种温度计量之间关系的函数表达式,并求摄氏温度为36时的华氏温度;
(3)当华氏温度为140时,摄氏温度为多少?
若设摄氏温度为S ?C,华氏温度为H ?F,则
H=1.8S+32.
当S=36时,H=96.8
因为H=1.8S+32=140,所以S=60.
例 1.如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
x
解:(1)y 是 x 的函数,自变量 x 的取值范围是x>0.
(2)y =2(x + )
典例精析
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出函数的图象吗?
x/m
1
2
3
4
5
6
y/m
26
16
14
14
14.8
16
40
35
30
25
20
15
10
5
5
10
O
x
y
(3)
已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少cm?
解:
x>0
(2)当x=10时,y=60÷10=6
x
y
60
=
(1)
做一做
例2 一个游泳池内有水300 m3,现打开排水管以每小时25 m3的排出量排水.
(1)写出游泳池内剩余水量Q m3与排水时间th间的函数关系式;
(2)写出自变量t的取值范围.
排水后的剩水量Q m3是排水时间h的函
数,有Q=-25 t +300.
池中共有300 m3水,每小时排水25 m3,故全部排完只需 300÷25=12(h),故自变量 t的取值范围是0≤t≤12.
(3)开始排水后的第5h末,游泳池中还有多少水?
(4)当游泳池中还剩150 m3水时,已经排水多长时间?
当t=5,代入上式得Q=-5×25+300=175(m3),
即第5h末池中还有水175 m3
当Q=150m3时,由150=-25 t +300,得t =6h,
即第6 h末池中有水150m3.
【归纳】实际问题中自变量的取值范围.
在实际问题中确定自变量的取值范围,主
要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
例 3.一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,
这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每
小时水位 .由此猜想,在这个时间
段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
5
(2)水位高度 y 是否为时间 t 的函数?如果是,试写
出一个符合表中数据的函数解析式,并画出函数图象.
这个函数能表示水位的变化规律吗?
(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: .
自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
(3)如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
已知火车站托运行李的费用C(元)和托运行李的重量P(千克)(P为整数)的对应关系如表:
做一做
P
1
2
3
4
5
…
C
2
2.5
3
3.5
4
…
(1)已知小周的所要托运的行李重12千克,请问小周托运行李的费用为多少元?
(2)写出C与P之间的函数解析式.
(3)小李托运行李花了15元钱,请问小李的行李重多少千克?
7.5元
C=0.5P+1.5
27千克
1.用列表法与表达式法表示n边形的内角和m(单位:度)是边数n的函数.
解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下:
n
3
4
5
6
…
m
…
所以m=(n-2)·180°(n≥3,且n为自然数).
180
360
540
720
提示:n边形的内角和公式是:(n-2) ×180°.
当堂练习
2.用表达式法与图象法表示等边三角形的周长l是边长a的函数.
a
…
1
2
3
4
…
l
…
3
6
9
12
…
描点、连线:
用描点法画函数l=3a的图象.
O
2
x
y
1
2
3
4
5
8
6
4
10
12
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为l=3a(a>0).
课堂小结
函数的初步应用
确定实际问题中函数关系式
描实际问题中的函数图像
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
