探索规律

(共30张PPT)
一只青蛙 1 张嘴，2 只眼睛 4 条腿，1 声扑通跳下水；
两只青蛙 2 张嘴，4 只眼睛 8 条腿，2 声扑通跳下水；
三只青蛙 3 张嘴，6 只眼睛12 条腿，3 声扑通跳下水；
十只青蛙__ 张嘴，__ 只眼睛__ 条腿，__ 声扑通跳下水；
…
一百只青蛙____张嘴，____只眼睛____条腿，____声扑通跳下水；
…
n只青蛙_____张嘴，_______只眼睛_______条腿，_______声扑通跳下水；
n
n
10
20
40
10
100
200
400
100
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
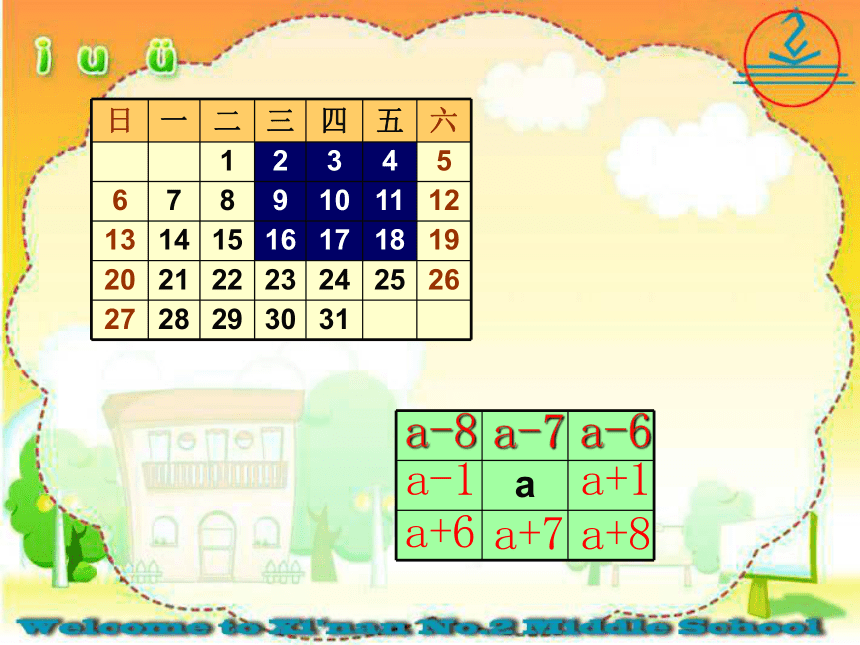
a
a-1
a+1
a-7
a+7
a+8
a-8
a-6
a+6
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
（江西省中考题）在上面的日历中，任意圈出一竖列相邻的三个数，设中间一个数为a,则这三个数之和为_________ （用含a的代数式表示）.
3a
-1、0、1、···、
一、数列：1、2、3、···、第n个数为：
。
（变式二）数列： 第n个数为：n-2
。
n
（变式一）数列：0、1、2、···、第n个数为：
。
n-1
4、6、8、···、
二、数列：2、4、6、···、第n个数为：
。
（变式二）数列： 第n个数为：2n+2
。
2n
（变式一）数列：0、2、4、···、第n个数为：
。
2n-2
5、7、9、···、
三、数列：1、3、5、···、第n个数为：
。
（变式二）数列： 第n个数为：2n+3
。
2n-1
（变式一）数列：3、5、7、···、第n个数为：
。
2n+1
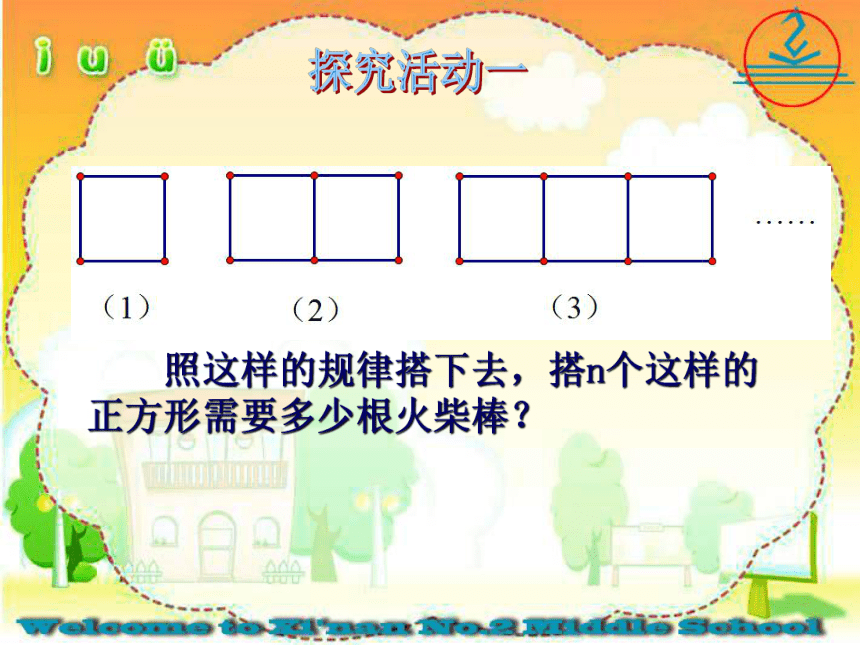
照这样的规律搭下去，搭n个这样的
正方形需要多少根火柴棒？
用火柴棒按下图的方式搭三角形
（2）照这样的规律搭下去，搭n个这样的
三角形需要多少根火柴棒？
（1）填写下表：
三角形个数 1 2 3 4 5
火柴棒根数
搭n个这样的三角形需要 (2n+1) 根火柴棒
3
11
9
5
7
观察下列图形：它们是按一定规律排列的，
依照此规律，第5个图形共有 个★，第6个图
形共有 个★．第n个图形共有 个★．
16
19
3n+1
第 2 个图形
（2011内蒙古乌兰察布）将一些半径相同的
小圆按如图所示的规律摆放，请仔细观察，第
n 个图形 有 个小圆.
（用含 n 的代数式表示）
第 1 个图形
第 3 个图形
第 4个图形
n(n+1)+4
（2009年娄底） 同学用火柴棒摆成如下的
三个“中”字形图案，依此规律，第n个“中”字形
图案需 根火柴棒.
6n+3
7
5
3
2
4
6
中间2不变
（2011广东肇庆）如图5所示，把同样大小的黑
色棋子摆放在正多边形的边上，按照这样的规律摆
下去，则第n（n是大于0的整数）个图形需要黑色棋
子的个数是 ．
温馨提示：（1）多边形的边数怎样变化？
（2）每边上的棋子怎样变化？
(n+1)(n+2)-(n+2)
数列四：2、4、8、16、···、第n个数是：
。
2n
。
（变式二）数列： 第n个数为：2n+1
（变式一）数列：1、2、4、···、第n个数为：
。
2n-1
4、8、16、···、
（变式三）数列：1、3、9、27···、第n个数为：
。
3n-1
填写对折次数与所得层数和所得折痕数的变化关系表：
对折次数 1 2 3 4 … n
所得层数
折痕条数
将一张普通的报纸对折，可得到一条折痕。继续对折，对折时每次折痕与上次的折痕保持平行。连续对折4次后，可以得到几条折痕？如果对折10次呢？对折n次呢。
2
4
8
16
2n
2n -1
7
3
1
15
…
…
数列五：1、4、9、16、···、第n个数是：
。
n2
。
（变式二）数列： 第n个数为:n2-1
（变式一）数列：2、5、10、···、第n个数为：
。
n2+1
0、3、8、···、
（变式三）数列：1、8、27···、第n个数为：
。
n3
（2011广东肇庆）如图5所示，把同样大小的黑色棋子
摆放在正多边形的边上，按照这样的规律摆下去，则第n
（n是大于0的整数）个图形需要黑色棋子的个数是 ．
3
8
15
24
联想：平方型数列
（n+1）2-1
(n+1)(n+2)-(n+2)
都是等差数列
都不是等差数列
做题方法
探索规律的一般步骤：
猜 想 规 律
表 示 规 律
验 证 规 律
观 察 特 例
分拆基本图形
分拆基本数列
1、按左图方式摆放餐桌和椅子
(1) 1张餐桌可坐___人;
2张餐桌可坐___人.
(2) 按照左图的方式继续排列餐桌,完成下表:
桌子
张数 1 2 3 4 5 … n
可坐
人数 …
6
10
14
18
22
6
10
试一试
4
4
+4
+4
+4
……
(4n+2)
n张餐桌可坐 人
3、研究下列算式，你发现了什么规律？
用字母表示这个规律。
1×3+1=22；
2×4+1=32；
3×5+1=42；
4×6+1=52；
……………
用n表示自然数,规律
是： 。
n(n+2)+1=(n+1)2
4、(2009年牡丹江市)有一列数 …，
那么第7个数是 。那么第n个数是 。
分子
分母
符号
（-1）n
（-1）n+1
这节课你有什么收获？
请和你的同桌进行交流。
探索规律时遇到挫折，你会怎么办？
不畏艰险，迎难而上！