5. 2.2 平行线的判定第一课时-人教版七年级数学下册课件(共21张PPT)
文档属性
| 名称 | 5. 2.2 平行线的判定第一课时-人教版七年级数学下册课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 14:30:23 | ||
图片预览




文档简介
人教版 数学七年级下册
第五章 相交线与平行线
5.2.2 平行线的判定(第一课时)
平行线的知识点回顾
同一平面内,不相交的两条直线叫做平行线。
a
b
平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”。
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a。
平行线的概念:
表示方法:
平行线的知识点回顾
平行线的性质(平行公理):
·
P
a
b
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
a
b
c
b
c
几何语言表达式:
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:
∵ a∥b, a∥c (已知)
∴ b∥c (平行线的传递性)
平行线的判定方法:
1.平行线的定义:
如果在同一平面内的两条直线不相交,那么这两条直线就互相平行。
2.平行公理:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
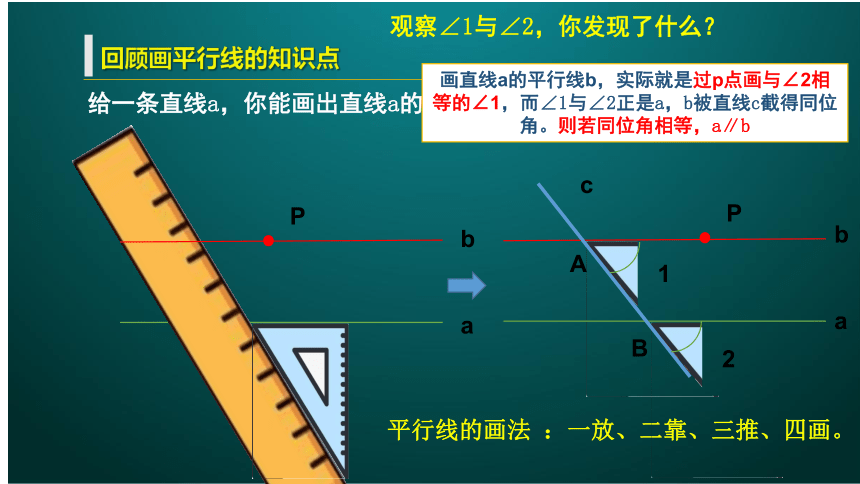
回顾画平行线的知识点
给一条直线a,你能画出直线a的平行线吗?
a
b
平行线的画法 :一放、二靠、三推、四画。
观察∠1与∠2,你发现了什么?
P
a
b
c
1
2
A
B
P
画直线a的平行线b,实际就是过p点画与∠2相等的∠1,而∠1与∠2正是a,b被直线c截得同位角。则若同位角相等,a∥b
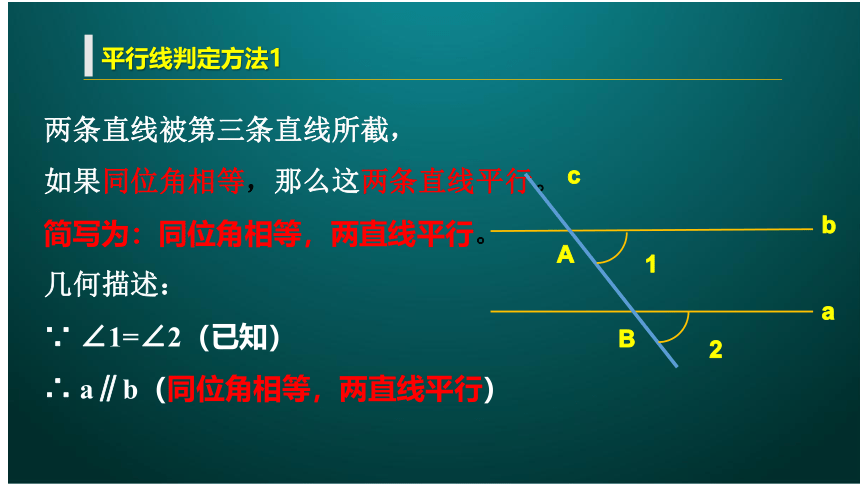
平行线判定方法1
两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。
简写为:同位角相等,两直线平行。
几何描述:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
a
b
c
1
2
A
B
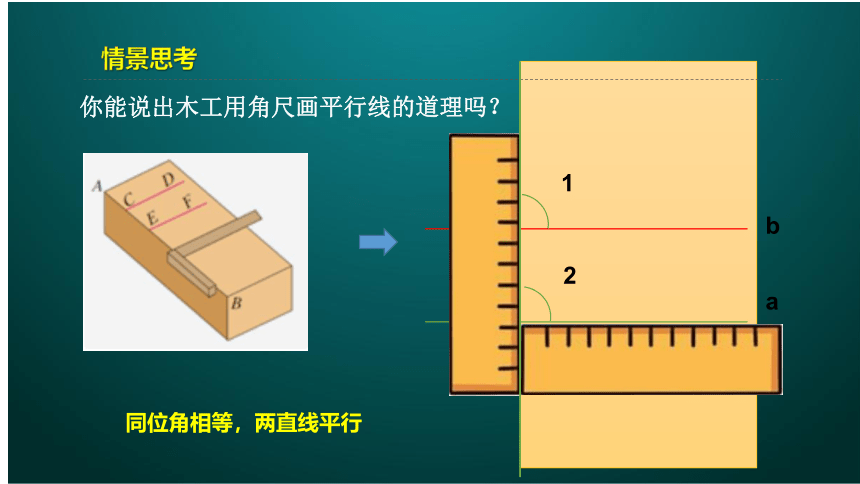
情景思考
你能说出木工用角尺画平行线的道理吗?
a
b
1
2
同位角相等,两直线平行
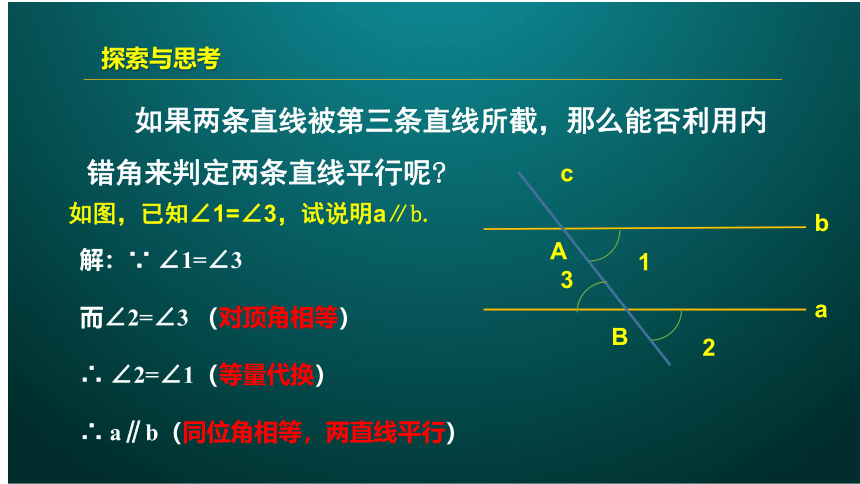
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
探索与思考
a
b
c
1
2
A
B
3
解:∵ ∠1=∠3
而∠2=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1=∠3,试说明a∥b.
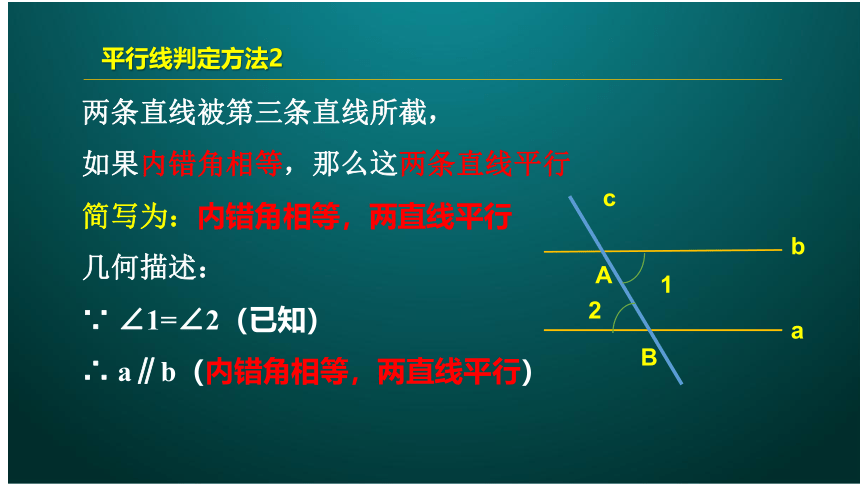
平行线判定方法2
两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行
简写为:内错角相等,两直线平行
几何描述:
∵ ∠1=∠2(已知)
∴ a∥b(内错角相等,两直线平行)
a
b
c
1
A
B
2
探索与思考
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
解:∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?(利用内错角知识证明)
探索与思考
a
b
c
1
2
A
B
3
解:∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(内错角相等,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
平行线判定方法3
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行
简写为:同旁内角互补,两直线平行
几何描述:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
a
b
c
1
A
B
2
已知条件:直线b与直线c都垂直于直线a.要说明的结论:直线b与直线c平行吗?
例1. 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
学会分析,应用方法:
在同一平面内,垂直于同一条直线的两条直线平行.
(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?
例2 如图, BE是AB的延长线.
答: AD∥BC .根据同位角相等,两直线平行.
例题讲解
(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?
例2 如图, BE是AB的延长线.
答: AE∥CD .根据内错角相等,两直线平行.
例题讲解
(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?
例2 如图, BE是AB的延长线.
答: AE∥CD .根据同旁内角互补,两直线平行.
例题讲解
例题讲解
例3 如图,已知直线a,b,c被d所截,∠1=72°,∠2=108°,∠3=72°,
试说明a∥b∥c。
例题讲解
例4 如图,已知CD⊥DA,AB⊥AD,∠1=∠2,问DF与AE平行吗?
例题讲解
例4(变式):如图,已知AB,CD被EF所截,∠1=∠2,∠CNF=∠BME,
试说明①AB∥CD ;②MP∥NQ
1
2
B
D
A
C
E
F
M
N
P
Q
课堂互动
Classroom Interaction
掌握判定直线平行的
三种方法
01
课后回顾
直线平行的三种判定方法的探究、逻辑推理及书面表达
02
初步了解转换的数学思想
03
1.课堂笔记整理
2.素养练习册----平行线的判定(第一课时)
课后作业:
第五章 相交线与平行线
5.2.2 平行线的判定(第一课时)
平行线的知识点回顾
同一平面内,不相交的两条直线叫做平行线。
a
b
平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”。
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a。
平行线的概念:
表示方法:
平行线的知识点回顾
平行线的性质(平行公理):
·
P
a
b
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
a
b
c
b
c
几何语言表达式:
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:
∵ a∥b, a∥c (已知)
∴ b∥c (平行线的传递性)
平行线的判定方法:
1.平行线的定义:
如果在同一平面内的两条直线不相交,那么这两条直线就互相平行。
2.平行公理:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
回顾画平行线的知识点
给一条直线a,你能画出直线a的平行线吗?
a
b
平行线的画法 :一放、二靠、三推、四画。
观察∠1与∠2,你发现了什么?
P
a
b
c
1
2
A
B
P
画直线a的平行线b,实际就是过p点画与∠2相等的∠1,而∠1与∠2正是a,b被直线c截得同位角。则若同位角相等,a∥b
平行线判定方法1
两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行。
简写为:同位角相等,两直线平行。
几何描述:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
a
b
c
1
2
A
B
情景思考
你能说出木工用角尺画平行线的道理吗?
a
b
1
2
同位角相等,两直线平行
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
探索与思考
a
b
c
1
2
A
B
3
解:∵ ∠1=∠3
而∠2=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1=∠3,试说明a∥b.
平行线判定方法2
两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行
简写为:内错角相等,两直线平行
几何描述:
∵ ∠1=∠2(已知)
∴ a∥b(内错角相等,两直线平行)
a
b
c
1
A
B
2
探索与思考
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
解:∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?(利用内错角知识证明)
探索与思考
a
b
c
1
2
A
B
3
解:∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(内错角相等,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
平行线判定方法3
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行
简写为:同旁内角互补,两直线平行
几何描述:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
a
b
c
1
A
B
2
已知条件:直线b与直线c都垂直于直线a.要说明的结论:直线b与直线c平行吗?
例1. 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
学会分析,应用方法:
在同一平面内,垂直于同一条直线的两条直线平行.
(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?
例2 如图, BE是AB的延长线.
答: AD∥BC .根据同位角相等,两直线平行.
例题讲解
(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?
例2 如图, BE是AB的延长线.
答: AE∥CD .根据内错角相等,两直线平行.
例题讲解
(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?
例2 如图, BE是AB的延长线.
答: AE∥CD .根据同旁内角互补,两直线平行.
例题讲解
例题讲解
例3 如图,已知直线a,b,c被d所截,∠1=72°,∠2=108°,∠3=72°,
试说明a∥b∥c。
例题讲解
例4 如图,已知CD⊥DA,AB⊥AD,∠1=∠2,问DF与AE平行吗?
例题讲解
例4(变式):如图,已知AB,CD被EF所截,∠1=∠2,∠CNF=∠BME,
试说明①AB∥CD ;②MP∥NQ
1
2
B
D
A
C
E
F
M
N
P
Q
课堂互动
Classroom Interaction
掌握判定直线平行的
三种方法
01
课后回顾
直线平行的三种判定方法的探究、逻辑推理及书面表达
02
初步了解转换的数学思想
03
1.课堂笔记整理
2.素养练习册----平行线的判定(第一课时)
课后作业:
