人教 版九年级数学下册 28.2.2 解直角三角形应用举例(第2课时)课件(共23张PPT)
文档属性
| 名称 | 人教 版九年级数学下册 28.2.2 解直角三角形应用举例(第2课时)课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 645.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
28.2.2应用举例(2)
方位角,坡度坡比
1、解直角三角形指什么?
2、解直角三角形主要依据什么?
在直角三角形中,除直角外还有五个元素,知道两个元素(至少有一个是边),就可以求出另三个未知元素的过程。
复习旧知
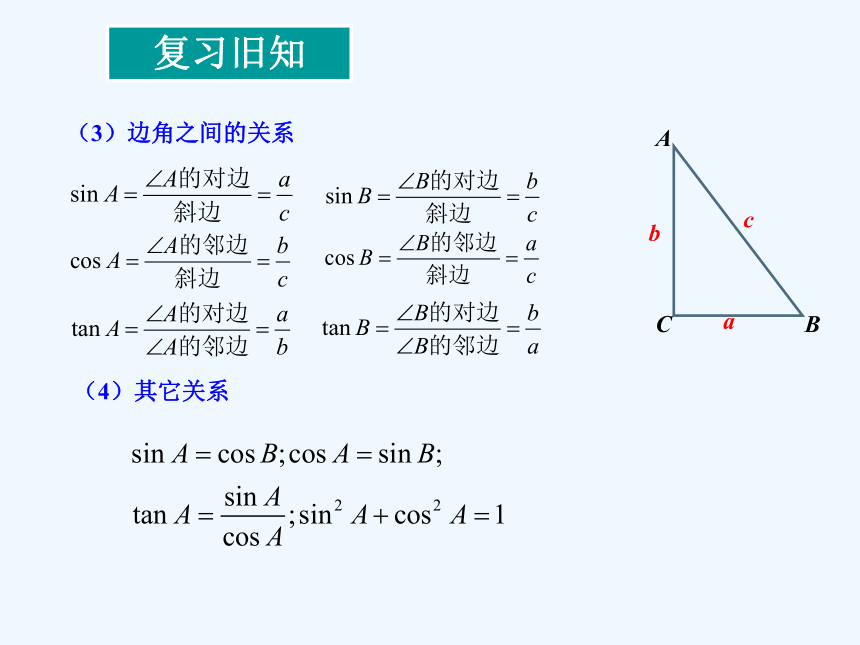
(3)边角之间的关系
A
B
a
b
c
C
复习旧知
(4)其它关系
指南或指北的方向线与目标方向线构成小于900的角,叫做方位角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
方位角
复习旧知
例1、
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80n
mine的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
解:如图
,在Rt△APC中,
PC=PA·cos(90°-60°)
=80×cos30°
在Rt△BPC中,∠B=30°
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约139n
mine.
60°
30°
P
B
C
A
例题讲解
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
1.如图,海中有一个小岛A,它的周围8n
mine内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12n
mine到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
解:由点A作BD的垂线交BD的延长线于点F,
垂足为F,∠AFD=90°
由题意图示可知∠DAF=30°
设DF=
x
,
AD=2x
则在Rt△ADF中,根据勾股定理
在Rt△ABF中,
解得x=6
10.4
>
8没有触礁危险
30°
60°
跟踪练习
如图,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即i=
.
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,即i=
=tan
a显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡度坡比
讲授新知
2、练习:
(1)一段坡面的坡角为60°,则坡度i=______;
跟踪练习
思考1:坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?
思考2:坡面水平宽度一定,铅直高度与坡度有何关系
?
思考
例2.
如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度
i=1:3是指DE与CE的比。根据图中数据求:
(1)坡角a和β的度数;
(2)斜坡AB的长(结果保留小数点后一位)
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:(1)在Rt△AFB中,∠AFB=90°
在Rt△CDE中,∠CED=90°
例题讲解
练习:3、
如图:是一海堤的横断面为梯形ABCD,已知堤顶宽BC为6m,堤高为3.2m,为了提高海堤的拦水能力,需要将海堤加高2m,并且保持堤顶宽度不变,迎水坡CD的坡度也不变。但是背水坡的坡度由原来的i=1:2改成i=1:2.5(有关数据在图上已注明)。
(1)求加高后的堤底HD的长。
(2)求增加部分的横断面积
(3)设大堤长为1000米,需多少方土加上去?
(4)若每方土300元,计划准备多少资金付给民工?
跟踪练习
图①
图②
图③
跟踪练习
(1):从图③中,你能求得这个横断面哪些量? 图②呢? 求堤底HD的长与图
③有关吗? 从图②中如何求出HD的长.
解:HD=HN+NF+DF=13+6+10.4=29.4(m)
答:加高后的堤底HD的长是29.4米
(2):如何求增加部分的面积?直接能求图①中阴影部分的面积吗?那么增加部分的面积与什么图形的面积有关?
跟踪练习
(3):
(4):
52360
300=15708000(元)
=1570.8(万元)
课内练习
课内练习
3.
去年“云娜”台风中心从我市(看成一个点A)的正东方向300km的B岛以每时25km的速度正面袭击我市,距台风中心250km的范围内均受台风的影响.我市遭到了严重的影响,那么影响时间有多长?
台风经过我市的路程-------刚好是一个半径为250km的圆的直径
解:
答:受台风影响的时间为20小时。
t=
r表示台风形成区域圆的半径
V表示风速
课内练习
4、今年“卡努”
台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?
课内练习
如图:若AD≤250km,则受台风影响;
若AD>250km,则不会受台风影响。
E
F
D
C
E
F
解:会受到影响。
以A为圆心,250km长为半径画圆交直线BC于E、F,
则DF=DE=200km,
∴
(小时)
答:影响时间为16小时。
250
连结AF,AE,
D
C
则∠ADB=900,AB=300km,∠ABD=300,
∴AD=150km,
作AD⊥BC于D,
∵150<250,∴会受到台风影响
4、今年“卡努”
台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?
课内练习
课堂小结
1、弄清俯角、仰角、坡度、坡角、水平距离、垂直距离、水位等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题?。
2、认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题。
3、选择合适的边角关系式,使计算尽可能简单,且不易出错。
4、按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位。
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
h
h
α
α
l
l
我们设法“化曲为直,以直代曲”.
我们可以把山坡“化整为零”地划分为一些小段,图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1.
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
h
α
l
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
28.2.2应用举例(2)
方位角,坡度坡比
1、解直角三角形指什么?
2、解直角三角形主要依据什么?
在直角三角形中,除直角外还有五个元素,知道两个元素(至少有一个是边),就可以求出另三个未知元素的过程。
复习旧知
(3)边角之间的关系
A
B
a
b
c
C
复习旧知
(4)其它关系
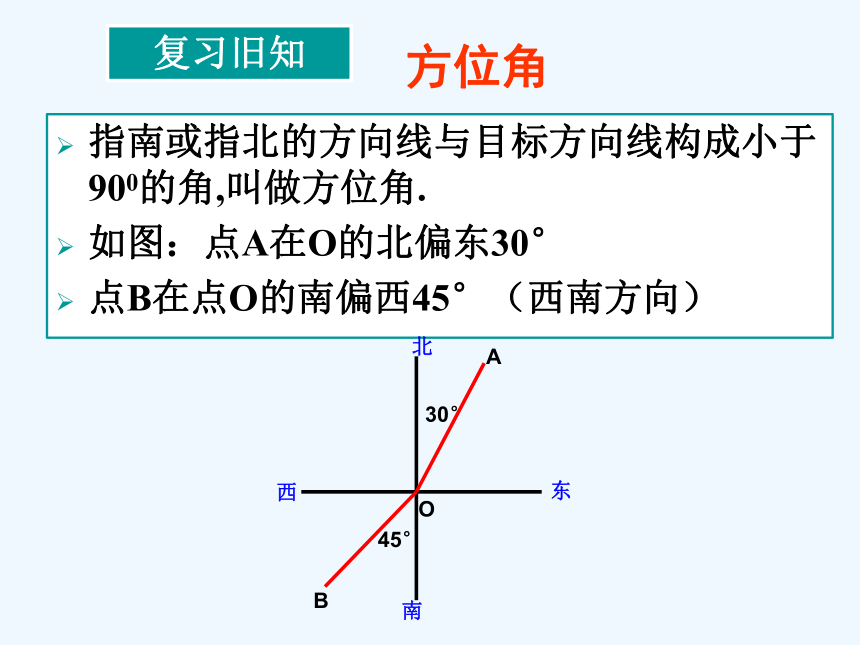
指南或指北的方向线与目标方向线构成小于900的角,叫做方位角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
方位角
复习旧知
例1、
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80n
mine的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
解:如图
,在Rt△APC中,
PC=PA·cos(90°-60°)
=80×cos30°
在Rt△BPC中,∠B=30°
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约139n
mine.
60°
30°
P
B
C
A
例题讲解
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
1.如图,海中有一个小岛A,它的周围8n
mine内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12n
mine到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
解:由点A作BD的垂线交BD的延长线于点F,
垂足为F,∠AFD=90°
由题意图示可知∠DAF=30°
设DF=
x
,
AD=2x
则在Rt△ADF中,根据勾股定理
在Rt△ABF中,
解得x=6
10.4
>
8没有触礁危险
30°
60°
跟踪练习
如图,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即i=
.
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,即i=
=tan
a显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡度坡比
讲授新知
2、练习:
(1)一段坡面的坡角为60°,则坡度i=______;
跟踪练习
思考1:坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?
思考2:坡面水平宽度一定,铅直高度与坡度有何关系
?
思考
例2.
如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度
i=1:3是指DE与CE的比。根据图中数据求:
(1)坡角a和β的度数;
(2)斜坡AB的长(结果保留小数点后一位)
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:(1)在Rt△AFB中,∠AFB=90°
在Rt△CDE中,∠CED=90°
例题讲解
练习:3、
如图:是一海堤的横断面为梯形ABCD,已知堤顶宽BC为6m,堤高为3.2m,为了提高海堤的拦水能力,需要将海堤加高2m,并且保持堤顶宽度不变,迎水坡CD的坡度也不变。但是背水坡的坡度由原来的i=1:2改成i=1:2.5(有关数据在图上已注明)。
(1)求加高后的堤底HD的长。
(2)求增加部分的横断面积
(3)设大堤长为1000米,需多少方土加上去?
(4)若每方土300元,计划准备多少资金付给民工?
跟踪练习
图①
图②
图③
跟踪练习
(1):从图③中,你能求得这个横断面哪些量? 图②呢? 求堤底HD的长与图
③有关吗? 从图②中如何求出HD的长.
解:HD=HN+NF+DF=13+6+10.4=29.4(m)
答:加高后的堤底HD的长是29.4米
(2):如何求增加部分的面积?直接能求图①中阴影部分的面积吗?那么增加部分的面积与什么图形的面积有关?
跟踪练习
(3):
(4):
52360
300=15708000(元)
=1570.8(万元)
课内练习
课内练习
3.
去年“云娜”台风中心从我市(看成一个点A)的正东方向300km的B岛以每时25km的速度正面袭击我市,距台风中心250km的范围内均受台风的影响.我市遭到了严重的影响,那么影响时间有多长?
台风经过我市的路程-------刚好是一个半径为250km的圆的直径
解:
答:受台风影响的时间为20小时。
t=
r表示台风形成区域圆的半径
V表示风速
课内练习
4、今年“卡努”
台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?
课内练习
如图:若AD≤250km,则受台风影响;
若AD>250km,则不会受台风影响。
E
F
D
C
E
F
解:会受到影响。
以A为圆心,250km长为半径画圆交直线BC于E、F,
则DF=DE=200km,
∴
(小时)
答:影响时间为16小时。
250
连结AF,AE,
D
C
则∠ADB=900,AB=300km,∠ABD=300,
∴AD=150km,
作AD⊥BC于D,
∵150<250,∴会受到台风影响
4、今年“卡努”
台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?
课内练习
课堂小结
1、弄清俯角、仰角、坡度、坡角、水平距离、垂直距离、水位等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题?。
2、认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题。
3、选择合适的边角关系式,使计算尽可能简单,且不易出错。
4、按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位。
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
h
h
α
α
l
l
我们设法“化曲为直,以直代曲”.
我们可以把山坡“化整为零”地划分为一些小段,图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1.
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
h
α
l
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
