人教版八年级数学下册18.2.3 正方形课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.2.3 正方形课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
初中数学八年级下册
18.2.3 正方形
生活中的正方形
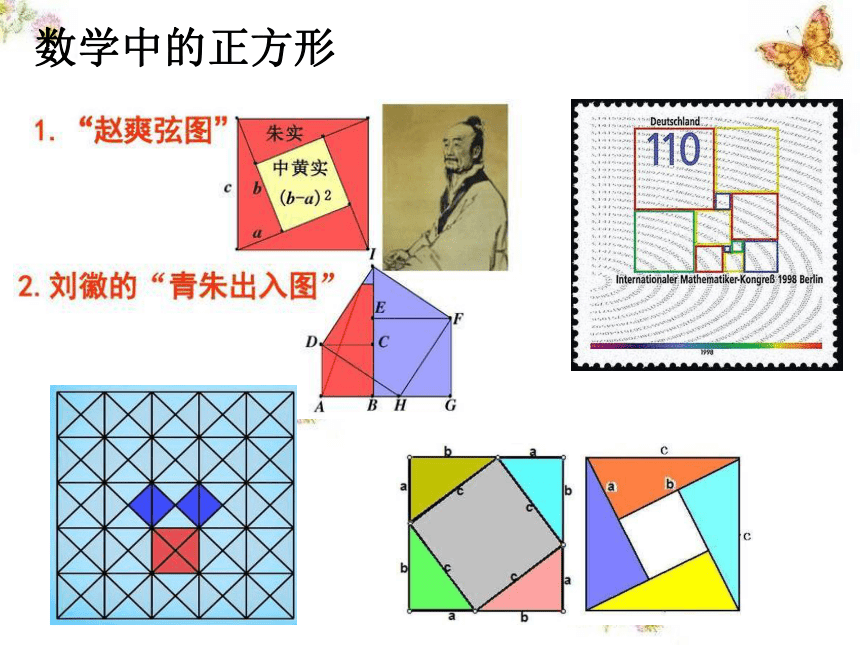
数学中的正方形
正方形
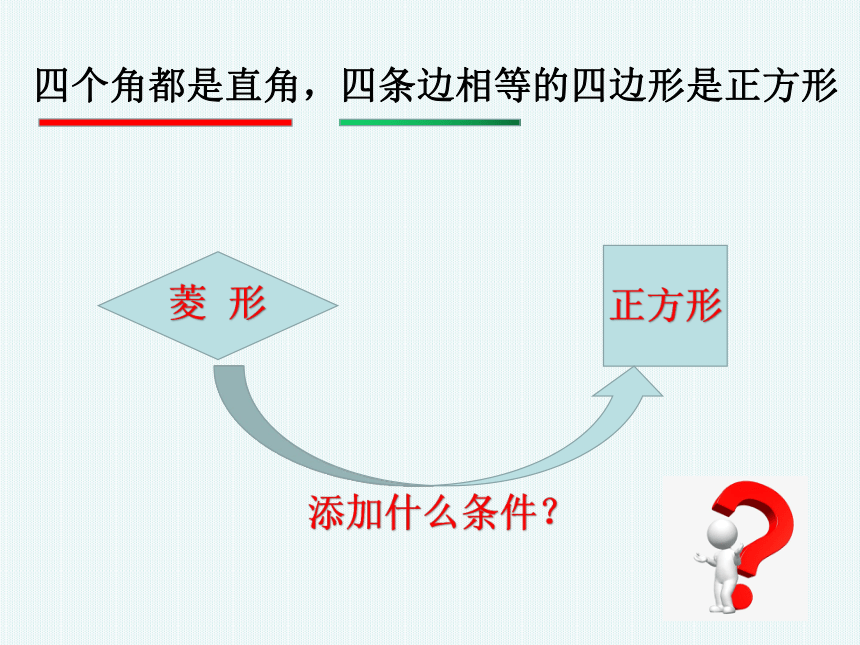
添加什么条件?
正方形:四个角都是直角,四条边相等
矩 形
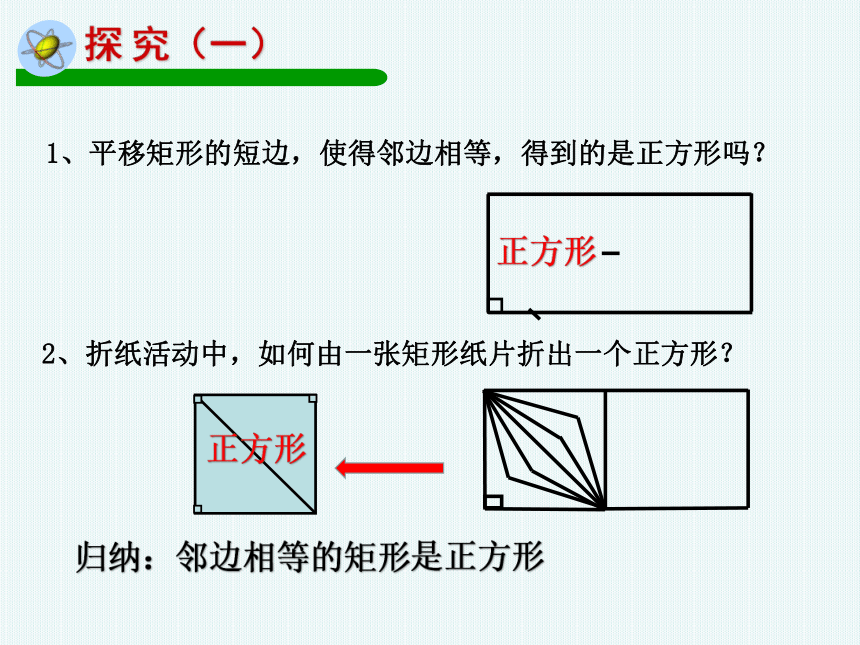
1、平移矩形的短边,使得邻边相等,得到的是正方形吗?
正方形
2、折纸活动中,如何由一张矩形纸片折出一个正方形?
归纳:邻边相等的矩形是正方形
探 究(一)
正方形
正方形
添加什么条件?
四个角都是直角,四条边相等的四边形是正方形
菱 形
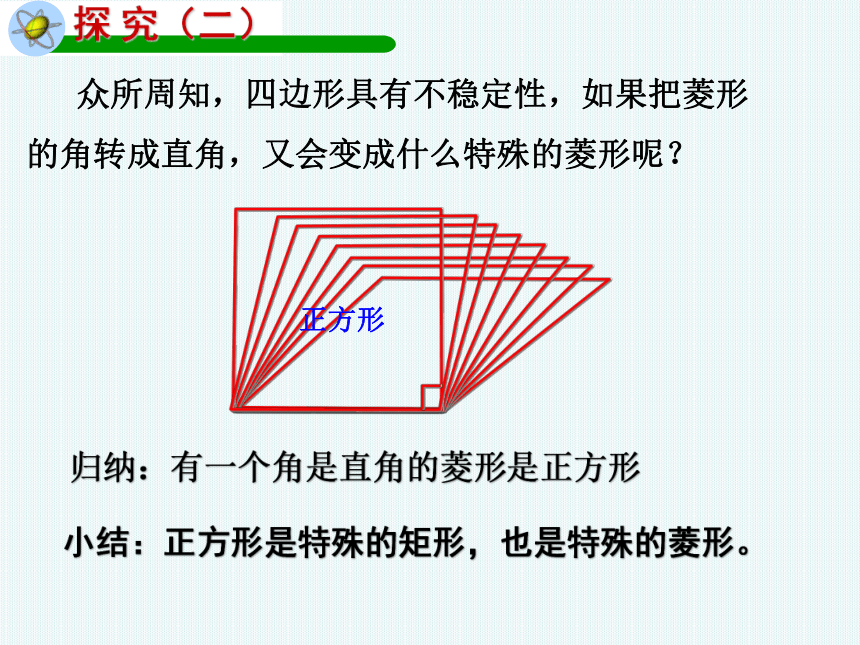
探 究(二)
正方形
众所周知,四边形具有不稳定性,如果把菱形
的角转成直角,又会变成什么特殊的菱形呢?
归纳:有一个角是直角的菱形是正方形
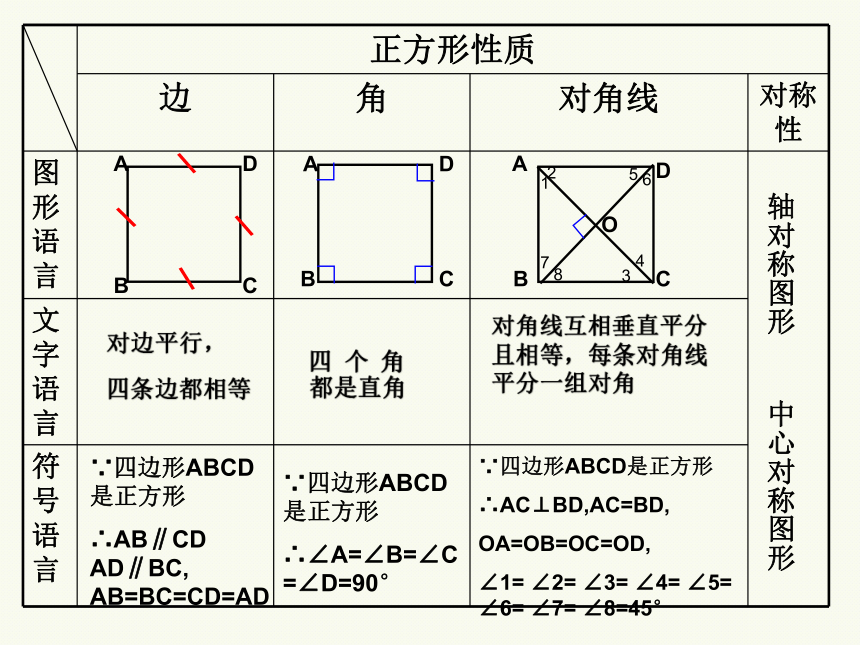
思考:正方形具有哪些性质?
正方形性质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
∟
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1= ∠2= ∠3= ∠4= ∠5= ∠6= ∠7= ∠8=45°
轴对称图形 中心对称图形
1
2
3
4
5
6
7
8
A
D
C
B
O
1. 正方形对角线把正方形分成多少个三角形?
它们是什么三角形?
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
试一试:正方形性质的应用
+ 有一个角是直角
+ 一组邻边相等
+ 对角线互相垂直
+ 对角线相等
一般四边形
+ 四条边相等、四个角是直角
2. 正方形OPQG的顶点O是正方形ABCD对角线的交
点,OP交AB于点E,OG交BC于点F,转动正方形OPQG,
AOE和 BOF有什么关系?
A
D
C
B
O
E
F
G
P
Q
△AOE≌△BOF
理由:
∵四边形ABCD是正方形
∴OA=OB,∠AOB=90°,
∠1=∠2=45° 又∵∠EOF=90°
∴∠AOB-∠3=∠EOF-∠3
即∠AOE=∠BOF
∴△AOE≌△BOF(ASA)
1
2
3
A
D
C
B
O
E
F
G
P
Q
3. 在转动过程中,两个正方形的重叠部分四边形OEBF
的面积有何变化?请说明理由。
4. 解决以上问题,用到了正方形的哪些性质?
面积不变
理由:
由上题得△AOE≌△BOF
∴S四边形OEBF=S△OEB+S△BOF
=S△AOB
= S正方ABCD
正方形的对角线互相垂直、
平分、每一条对角线平分一
组对角,正方形的角是直角
5. 已知:如图,点G是正方形ABCD的边BC上的任意一点,
DE⊥AG于点E,BF//DE,交AG于点F.
求证:AF-BF=EF
A
B
C
D
E
F
G
证明:∵DE⊥AG, ∴∠DEF=∠1+∠2=90°
∵DE//BF, ∴∠DEF=∠BFE=90°
∵四边形ABCD是正方形
∴AB=AD,∠BAD=∠1+∠3=90°
∴∠2=∠3
又∠AED=∠AFB=90°
∴ △AED≌△BFA(AAS)
∴AE=BF
∴AF-AE=AF-BF=EF
解决以上问题,用到了正方形的哪些性质?
1
2
3
正方形四条边相等、
角是直角
探 究(四):正方形的判定
+ 有一个角是直角
+ 一组邻边相等
+ 对角线互相垂直
+ 对角线相等
一般四边形
+ 四条边相等、四个角是直角
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
①EB//CF,CE//BF;
②BE=CE,BE=BF;
③BE//CF,CE⊥BE;
④BE=CE,CE//BF.
其中能判定四边形BECF是正方形的是
A
B
C
D
F
E
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
①EB//CF,CE//BF;
A
B
C
D
F
E
1
2
分析:
根据添加的条件EB//CF,CE//BF,
可得四边形FBEC是平行四边形
由已知条件,可得 ∠1=∠2=45°,
∴∠F=90° ∴ FBEC是矩形
∵∠1=∠2, CF=BF
∴矩形FBEC是正方形
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
②BE=CE,BE=BF;
A
B
C
D
F
E
1
2
分析:
由已知条件,可得 ∠1=∠2,∴CF=BF
根据添加的条件BE=CE,BE=BF
BE=CE=BF=CF
∴四边形FBEC是菱形
∵∠1=∠2=45°,∴∠F=90°
∴菱形FBEC是正方形
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
③BE//CF,CE⊥BE;
A
B
C
D
F
E
1
2
分析:
由已知条件,可得 ∠1=∠2=45°,∴∠F=90°
根据添加的条件EB//CF,得∠1=∠3=45°
∴∠2+∠3=90°即∠FBE=90°
根据添加的条件CE⊥BE,得∠E=90°
∴四边形FBEC是矩形
∵∠1=∠2,∴ CF=BF
∴矩形FBEC是正方形
3
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
④BE=CE,CE//BF.
A
B
C
D
F
E
1
2
分析:
根据添加的条件CE//BF,得∠2=∠3=45°
BE=CE,得∠4=∠3=45°,进而得∠E=90°
∴∠E=∠FBE=∠ECF=90°
∴四边形FBEC是矩形
∵∠1=∠2,∴ CF=BF
∴矩形FBEC是正方形
3
4
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
①EB//CF,CE//BF;
②BE=CE,BE=BF;
③BE//CF,CE⊥BE;
④BE=CE,CE//BF.
其中能判定四边形BECF是正方形的是①②③④
A
B
C
D
F
E
A
B
C
D
M
N
E
F
2. 如图,E、F、M、N分别是正方形ABCD四边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
四边形EFMN是正方形
证明:∵四边形ABCD是正方形
∴AB=BC=CD=DA, ∠A=∠B=90°
∵AE=BF=CM=DN, ∴ NA=EB ∴△AEN≌△BFE(ASA)
∴NE=EF , ∠1=∠2
∵∠1+∠3=90°
∴∠2+∠3=90°,即∠NEF=90°
同理:EF=FM=MN=NE,
∠EFM=∠FMN=∠FMN=∠MNE=90°
∴四边形EFMN是正方形
1
2
3
初中数学八年级下册
18.2.3 正方形
生活中的正方形
数学中的正方形
正方形
添加什么条件?
正方形:四个角都是直角,四条边相等
矩 形
1、平移矩形的短边,使得邻边相等,得到的是正方形吗?
正方形
2、折纸活动中,如何由一张矩形纸片折出一个正方形?
归纳:邻边相等的矩形是正方形
探 究(一)
正方形
正方形
添加什么条件?
四个角都是直角,四条边相等的四边形是正方形
菱 形
探 究(二)
正方形
众所周知,四边形具有不稳定性,如果把菱形
的角转成直角,又会变成什么特殊的菱形呢?
归纳:有一个角是直角的菱形是正方形
思考:正方形具有哪些性质?
正方形性质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
∟
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD,
∠1= ∠2= ∠3= ∠4= ∠5= ∠6= ∠7= ∠8=45°
轴对称图形 中心对称图形
1
2
3
4
5
6
7
8
A
D
C
B
O
1. 正方形对角线把正方形分成多少个三角形?
它们是什么三角形?
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
试一试:正方形性质的应用
+ 有一个角是直角
+ 一组邻边相等
+ 对角线互相垂直
+ 对角线相等
一般四边形
+ 四条边相等、四个角是直角
2. 正方形OPQG的顶点O是正方形ABCD对角线的交
点,OP交AB于点E,OG交BC于点F,转动正方形OPQG,
AOE和 BOF有什么关系?
A
D
C
B
O
E
F
G
P
Q
△AOE≌△BOF
理由:
∵四边形ABCD是正方形
∴OA=OB,∠AOB=90°,
∠1=∠2=45° 又∵∠EOF=90°
∴∠AOB-∠3=∠EOF-∠3
即∠AOE=∠BOF
∴△AOE≌△BOF(ASA)
1
2
3
A
D
C
B
O
E
F
G
P
Q
3. 在转动过程中,两个正方形的重叠部分四边形OEBF
的面积有何变化?请说明理由。
4. 解决以上问题,用到了正方形的哪些性质?
面积不变
理由:
由上题得△AOE≌△BOF
∴S四边形OEBF=S△OEB+S△BOF
=S△AOB
= S正方ABCD
正方形的对角线互相垂直、
平分、每一条对角线平分一
组对角,正方形的角是直角
5. 已知:如图,点G是正方形ABCD的边BC上的任意一点,
DE⊥AG于点E,BF//DE,交AG于点F.
求证:AF-BF=EF
A
B
C
D
E
F
G
证明:∵DE⊥AG, ∴∠DEF=∠1+∠2=90°
∵DE//BF, ∴∠DEF=∠BFE=90°
∵四边形ABCD是正方形
∴AB=AD,∠BAD=∠1+∠3=90°
∴∠2=∠3
又∠AED=∠AFB=90°
∴ △AED≌△BFA(AAS)
∴AE=BF
∴AF-AE=AF-BF=EF
解决以上问题,用到了正方形的哪些性质?
1
2
3
正方形四条边相等、
角是直角
探 究(四):正方形的判定
+ 有一个角是直角
+ 一组邻边相等
+ 对角线互相垂直
+ 对角线相等
一般四边形
+ 四条边相等、四个角是直角
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
①EB//CF,CE//BF;
②BE=CE,BE=BF;
③BE//CF,CE⊥BE;
④BE=CE,CE//BF.
其中能判定四边形BECF是正方形的是
A
B
C
D
F
E
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
①EB//CF,CE//BF;
A
B
C
D
F
E
1
2
分析:
根据添加的条件EB//CF,CE//BF,
可得四边形FBEC是平行四边形
由已知条件,可得 ∠1=∠2=45°,
∴∠F=90° ∴ FBEC是矩形
∵∠1=∠2, CF=BF
∴矩形FBEC是正方形
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
②BE=CE,BE=BF;
A
B
C
D
F
E
1
2
分析:
由已知条件,可得 ∠1=∠2,∴CF=BF
根据添加的条件BE=CE,BE=BF
BE=CE=BF=CF
∴四边形FBEC是菱形
∵∠1=∠2=45°,∴∠F=90°
∴菱形FBEC是正方形
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
③BE//CF,CE⊥BE;
A
B
C
D
F
E
1
2
分析:
由已知条件,可得 ∠1=∠2=45°,∴∠F=90°
根据添加的条件EB//CF,得∠1=∠3=45°
∴∠2+∠3=90°即∠FBE=90°
根据添加的条件CE⊥BE,得∠E=90°
∴四边形FBEC是矩形
∵∠1=∠2,∴ CF=BF
∴矩形FBEC是正方形
3
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
④BE=CE,CE//BF.
A
B
C
D
F
E
1
2
分析:
根据添加的条件CE//BF,得∠2=∠3=45°
BE=CE,得∠4=∠3=45°,进而得∠E=90°
∴∠E=∠FBE=∠ECF=90°
∴四边形FBEC是矩形
∵∠1=∠2,∴ CF=BF
∴矩形FBEC是正方形
3
4
试一试:正方形判定的应用
1.如图,矩形ABCD内一点F,FB与FC分别平分∠ABC
和∠BCD,点E为矩形ABCD外一点,连接BE,CE,
现添加下列条件:
①EB//CF,CE//BF;
②BE=CE,BE=BF;
③BE//CF,CE⊥BE;
④BE=CE,CE//BF.
其中能判定四边形BECF是正方形的是①②③④
A
B
C
D
F
E
A
B
C
D
M
N
E
F
2. 如图,E、F、M、N分别是正方形ABCD四边上的点,且AE=BF=CM=DN.试判断四边形EFMN是什么图形,并证明你的结论.
四边形EFMN是正方形
证明:∵四边形ABCD是正方形
∴AB=BC=CD=DA, ∠A=∠B=90°
∵AE=BF=CM=DN, ∴ NA=EB ∴△AEN≌△BFE(ASA)
∴NE=EF , ∠1=∠2
∵∠1+∠3=90°
∴∠2+∠3=90°,即∠NEF=90°
同理:EF=FM=MN=NE,
∠EFM=∠FMN=∠FMN=∠MNE=90°
∴四边形EFMN是正方形
1
2
3
