人教版八年级数学下册第十八章 18.1.2平行四边形的判定课件(共21张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十八章 18.1.2平行四边形的判定课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 112.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览





文档简介
第十八章
平行四边形
18.1.2 平行四边形的判定
1
复 习 回 顾
思考:平行四边形的性质有哪些?
平 行 四 边 形
边
角
对角线
a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
平行四边形两组对角分别相等.
平行四边形对角线互相平分 .
2
新 知 导 入
思考:平行四边形的定义是什么?
两组对边分别平行的四边形叫做平行四边形
思考:给你一个四边形,你怎样证明它是一个平行四边形呢?
数学语言:
∵AB//CD,AD//BC;
∴四边形ABCD是平行四边形。
提示:从平行四边的定义下手,利用命题(逆命题、逆否命题)
3
新 知 导 入
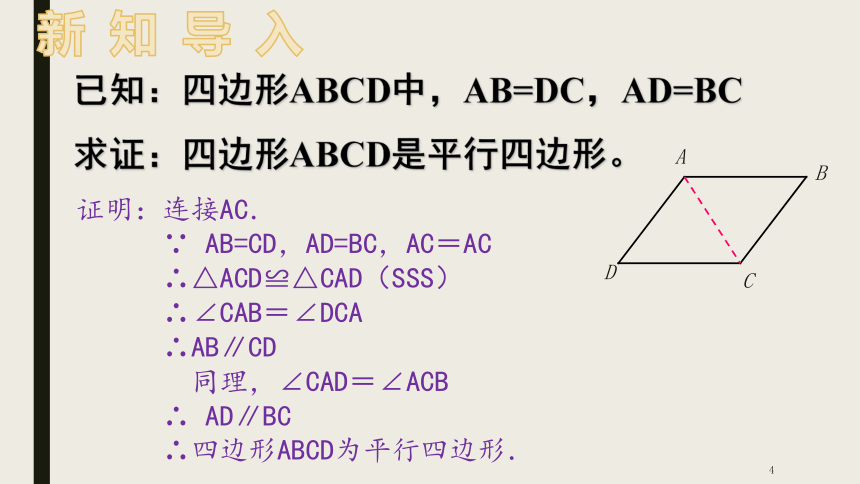
已知:四边形ABCD中,AB=DC,AD=BC
求证:四边形ABCD是平行四边形。
A
C
B
D
证明:连接AC.
∵ AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴ AD∥BC
∴四边形ABCD为平行四边形.
4
新 知 导 入
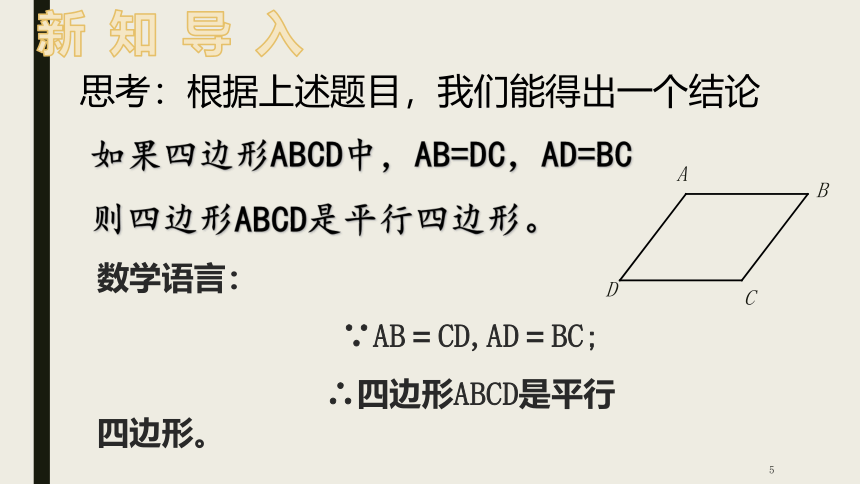
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,AB=DC,AD=BC
则四边形ABCD是平行四边形。
数学语言:
∵AB=CD,AD=BC;
∴四边形ABCD是平行四边形。
A
C
B
D
5
新 知 导 入
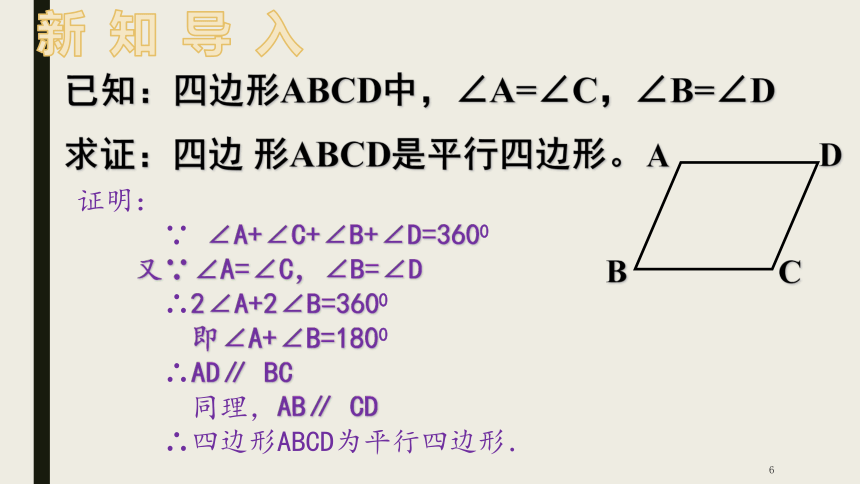
已知:四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边 形ABCD是平行四边形。
A
B
C
D
证明:
∵ ∠A+∠C+∠B+∠D=3600
又∵∠A=∠C,∠B=∠D
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴AD∥ BC
同理,AB∥ CD
∴四边形ABCD为平行四边形.
6
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,∠A=∠C,∠B=∠D
则四边形ABCD是平行四边形。
新 知 导 入
A
B
C
D
数学语言:
∵∠A=∠C,∠B=∠D;
∴四边形ABCD是平行四边形。
7
新 知 导 入
已知:四边形ABCD中,OA=OC,OB=OD
求证:四边形ABCD是平行四边形.
A
B
C
D
O
证明:
在△AOB和△COD中,
OA=OC (已知)
OB=OD (已知)
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
8
新 知 导 入
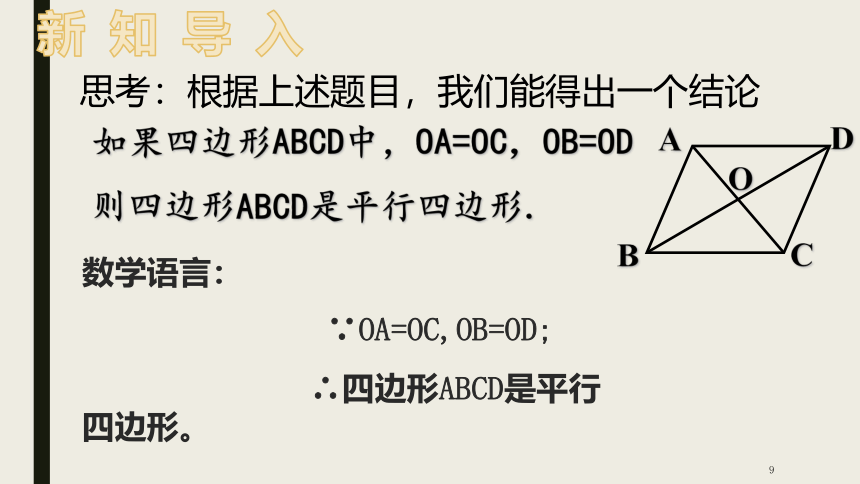
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,OA=OC,OB=OD
则四边形ABCD是平行四边形.
A
B
C
D
O
数学语言:
∵OA=OC,OB=OD;
∴四边形ABCD是平行四边形。
9
新 知 导 入
已知:四边形ABCD中,AD=BC,AD∥BC
求证:四边形ABCD是平行四边形
A
B
C
D
在△ABC和△CDA中,
AD=BC (已知)
AC=CA (公共边)
∠DAC=∠2BCA(已证)
∴△ABC≌△CDA(SAS)
∴ AB=CD
∴四边形ABCD是平行四边形。
∵AB∥ CD
∴ ∠DAC=∠BCA
又∵AD=BC
证明:连接AC
10
新 知 导 入
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,AD=BC,AD∥BC
则四边形ABCD是平行四边形
A
B
C
D
数学语言:
∵AD=BC,AD∥BC;
∴四边形ABCD是平行四边形。
11
归 纳 总 结
平 行 四 边 形 的 判 定
判定 1 定义:两组对边分别平行的四边形是平行四边形。
判定3 两组对角分别相等的四边形是平行四边形。
判定4 两条对角线互相平分的四边形是平行四边形。
判定2 两组对边分别相等的四边形是平行四边形。
判定5 一组对边平行且相等的四边形是平行四边形。
12
新 知 导 入
定义:连接三角形两边中点的线段叫做三角形的中位线.
三角形的中位线
思考:
(1)一个三角形的中位线共有几条?
(2)三角形的中位线与中线有什么区别?
13
新 知 导 入
性质:三角形的中位线平行与第三边,且等于第三边的一半.
三角形中位线的性质
14
典 例 剖 析
在下列条件中,不能判定四边形是平行四边形的是( )
A.AB∥CD,AD∥BC
B. AB=CD,AD=BC
C.AB∥CD,AB=CD
D. AB∥CD,AD=BC
D
15
典 例 剖 析
根据下列条件,不能判定一个四边形为平行四边形的是( )
A.两组对边分别相等
B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行
C
16
如图四边形ABCD中,AB//CD,只需添加一个条件,能使四边形ABCD是平行四边形,现有条件:
①AB=CD,②BC=AD,③AD//BC,④∠ABC=∠ADC,
这些条件中,满足要求的有( )
A.1个 B.2个 C.3个 D.4个
典 例 剖 析
A
C
B
D
C
17
典 例 剖 析
已知:如图,E,F分别是平行四边形的边AD,BC的中点。
求证:BE=DF.
F
E
C
B
A
D
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED平行且相等BF.
∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
18
典 例 剖 析
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
19
典 例 剖 析
已知:在平行四边形ABCD中,E,F分别是AD,BC的中点,M,N在CB,AD的延长线上,且BM=DN.
求证:EM=FN.
E
M
D
N
F
C
A
B
20
典 例 剖 析
(1)已知:平行四边形ABCD中,E、F分别是边AD、BC的中点;求证:EB=DF.
(2)在(1)的图中,AF交BE于G,CE交DF于H;求证:EF与GH相互平分.
H
G
F
E
D
C
B
A
21
平行四边形
18.1.2 平行四边形的判定
1
复 习 回 顾
思考:平行四边形的性质有哪些?
平 行 四 边 形
边
角
对角线
a.平行四边形两组对边分别平行.
b.平行四边形两组对边分别相等.
平行四边形两组对角分别相等.
平行四边形对角线互相平分 .
2
新 知 导 入
思考:平行四边形的定义是什么?
两组对边分别平行的四边形叫做平行四边形
思考:给你一个四边形,你怎样证明它是一个平行四边形呢?
数学语言:
∵AB//CD,AD//BC;
∴四边形ABCD是平行四边形。
提示:从平行四边的定义下手,利用命题(逆命题、逆否命题)
3
新 知 导 入
已知:四边形ABCD中,AB=DC,AD=BC
求证:四边形ABCD是平行四边形。
A
C
B
D
证明:连接AC.
∵ AB=CD,AD=BC,AC=AC
∴△ACD≌△CAD(SSS)
∴∠CAB=∠DCA
∴AB∥CD
同理,∠CAD=∠ACB
∴ AD∥BC
∴四边形ABCD为平行四边形.
4
新 知 导 入
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,AB=DC,AD=BC
则四边形ABCD是平行四边形。
数学语言:
∵AB=CD,AD=BC;
∴四边形ABCD是平行四边形。
A
C
B
D
5
新 知 导 入
已知:四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边 形ABCD是平行四边形。
A
B
C
D
证明:
∵ ∠A+∠C+∠B+∠D=3600
又∵∠A=∠C,∠B=∠D
∴2∠A+2∠B=3600
即∠A+∠B=1800
∴AD∥ BC
同理,AB∥ CD
∴四边形ABCD为平行四边形.
6
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,∠A=∠C,∠B=∠D
则四边形ABCD是平行四边形。
新 知 导 入
A
B
C
D
数学语言:
∵∠A=∠C,∠B=∠D;
∴四边形ABCD是平行四边形。
7
新 知 导 入
已知:四边形ABCD中,OA=OC,OB=OD
求证:四边形ABCD是平行四边形.
A
B
C
D
O
证明:
在△AOB和△COD中,
OA=OC (已知)
OB=OD (已知)
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形。
8
新 知 导 入
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,OA=OC,OB=OD
则四边形ABCD是平行四边形.
A
B
C
D
O
数学语言:
∵OA=OC,OB=OD;
∴四边形ABCD是平行四边形。
9
新 知 导 入
已知:四边形ABCD中,AD=BC,AD∥BC
求证:四边形ABCD是平行四边形
A
B
C
D
在△ABC和△CDA中,
AD=BC (已知)
AC=CA (公共边)
∠DAC=∠2BCA(已证)
∴△ABC≌△CDA(SAS)
∴ AB=CD
∴四边形ABCD是平行四边形。
∵AB∥ CD
∴ ∠DAC=∠BCA
又∵AD=BC
证明:连接AC
10
新 知 导 入
思考:根据上述题目,我们能得出一个结论
如果四边形ABCD中,AD=BC,AD∥BC
则四边形ABCD是平行四边形
A
B
C
D
数学语言:
∵AD=BC,AD∥BC;
∴四边形ABCD是平行四边形。
11
归 纳 总 结
平 行 四 边 形 的 判 定
判定 1 定义:两组对边分别平行的四边形是平行四边形。
判定3 两组对角分别相等的四边形是平行四边形。
判定4 两条对角线互相平分的四边形是平行四边形。
判定2 两组对边分别相等的四边形是平行四边形。
判定5 一组对边平行且相等的四边形是平行四边形。
12
新 知 导 入
定义:连接三角形两边中点的线段叫做三角形的中位线.
三角形的中位线
思考:
(1)一个三角形的中位线共有几条?
(2)三角形的中位线与中线有什么区别?
13
新 知 导 入
性质:三角形的中位线平行与第三边,且等于第三边的一半.
三角形中位线的性质
14
典 例 剖 析
在下列条件中,不能判定四边形是平行四边形的是( )
A.AB∥CD,AD∥BC
B. AB=CD,AD=BC
C.AB∥CD,AB=CD
D. AB∥CD,AD=BC
D
15
典 例 剖 析
根据下列条件,不能判定一个四边形为平行四边形的是( )
A.两组对边分别相等
B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行
C
16
如图四边形ABCD中,AB//CD,只需添加一个条件,能使四边形ABCD是平行四边形,现有条件:
①AB=CD,②BC=AD,③AD//BC,④∠ABC=∠ADC,
这些条件中,满足要求的有( )
A.1个 B.2个 C.3个 D.4个
典 例 剖 析
A
C
B
D
C
17
典 例 剖 析
已知:如图,E,F分别是平行四边形的边AD,BC的中点。
求证:BE=DF.
F
E
C
B
A
D
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED平行且相等BF.
∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
18
典 例 剖 析
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
19
典 例 剖 析
已知:在平行四边形ABCD中,E,F分别是AD,BC的中点,M,N在CB,AD的延长线上,且BM=DN.
求证:EM=FN.
E
M
D
N
F
C
A
B
20
典 例 剖 析
(1)已知:平行四边形ABCD中,E、F分别是边AD、BC的中点;求证:EB=DF.
(2)在(1)的图中,AF交BE于G,CE交DF于H;求证:EF与GH相互平分.
H
G
F
E
D
C
B
A
21
