人教版八年级数学下册课件:18.2特殊的平行四边形—2.3正方形(1)(共25张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2特殊的平行四边形—2.3正方形(1)(共25张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览







文档简介
复习备用
1.定义:两组对边分别平行;
2.两组对边分别相等.
平行四边形的性质
边:
对角线:
角:
对角相等,邻角互补.
对角线互相平分
平行四边形是
特殊的四边形,具有
四边形的一切性质
问题引入
矩形的性质
边:
对角线:
角:
矩形是特殊的平
行四边形,具有平
行四边形的一切性质
复习引入
菱形的性质
边:
对角线:
角:
菱形是特殊的平
行四边形,具有平
行四边形的一切性质
问题引入
正方形*自我介绍
在四边形的大家庭中,我有四个兄弟.
老大是平行四边形,它性格温和;
老二是菱形,它活泼可爱;
老三是矩形,它稳重大方,江湖上人称长方形;
我就是正方形老四,我集三位大哥的优点于一身,人见人爱.
人教版八年级数学下册
第十八章 平行四边形
18.2 特殊的平行四边形
2.3 正方形(1)
——正方形及其性质
1.知道正方形与平行四边形、矩形、菱形的关系.
2.能从边、内角、对角线三个方面掌握正方形的所有性质.
重点:正方形的性质.
难点:正方形的性质在几何问题中的运用.
学习目标
重点难点
知识点一:正方形的定义
新知探究
矩形
邻边
相等
有一组邻边相等的矩形是正方形
正方形
■正方形是特殊的矩形▆
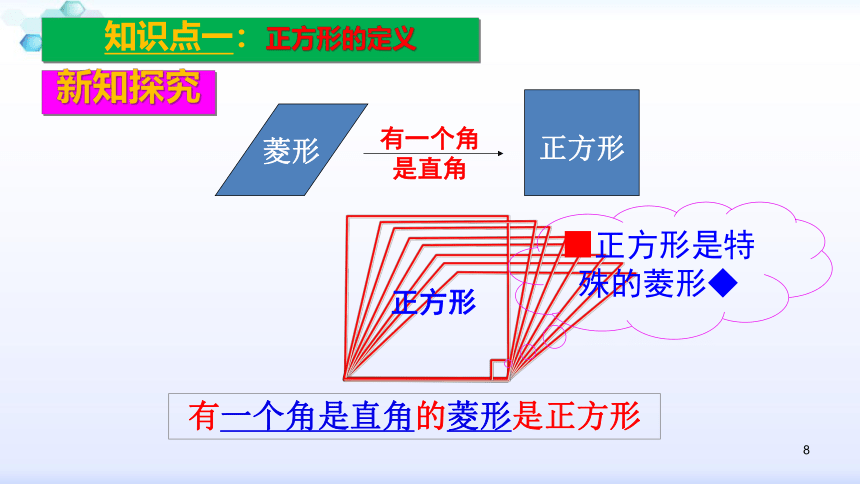
知识点一:正方形的定义
新知探究
正方形
菱形
正方形
有一个角是直角
■正方形是特殊的菱形◆
有一个角是直角的菱形是正方形
新知归纳
?有一组邻边相等的矩形是正方形;
?有一个角是直角的菱形是正方形;
?有一组邻边相等并且有一个角是直角的平行四边形是正方形.
知识点一:正方形的定义
学以致用
1.下面四个定义中不正确的是( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
B
知识点一:正方形的定义
2.已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C.AD=BC D.BC=CD
3.下列说法错误的是( )
A.正方形是平行四边形 B.正方形是菱形
C.正方形是矩形 D.菱形和矩形都是正方形
D
学以致用
知识点一:正方形的定义
D
归纳总结
知识点一:正方形的定义
平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
新知探究
?探究:正方形不仅是特殊的平行四边形而且是特殊的矩形、特殊的菱形,它具有哪些性质呢?
知识点二:正方形的性质
新知归纳
知识点二:正方形的性质
四条边都相等,对边平行.
正方形
的性质
边:
对角线:
角:
四个角都是直角.
对角线相等且互相垂直平分,而且每条对角线平分没有组对角.
典例讲评
例1 如图,已知点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF. 求证:DE=BE.
知识点二:正方形的性质
证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=∠BAD=90°.
∴∠BAE+∠EAD=90°.
∴EA⊥AF, ∴∠BAE+∠FAB=90°.
∴∠EAD=∠FAB.
∴△ABF≌△ADE. ∴DE=BF.
互动探究? 正方形的性质
1.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD= 度.
合作探究
知识点二:正方形的性质
22.5
互动探究? 正方形的性质
2.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF.
(2)若∠ABE=55°,求∠EGC的大小.
合作探究
知识点二:正方形的性质
归纳总结
知识点二:正方形的性质
通过证明三角形全等得到边和角相等,再进一步得到平行或垂直,是有关正方形中证边或角相等的最常用的方法,而正方形的四条边相等,四个角都是直角为证明三角形全等提供了条件.
学以致用
1. 正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.四条边相等
C.对角线相等 D.对角线互相平分
2.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.
若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4 C.5 D.6
B
B
知识点二:正方形的性质
学以致用
3.把图①中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图②、图③所示的正方形,则图①中菱形的面积为 .
12
知识点二:正方形的性质
学以致用
4.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
5.如图,正方形ABCD中,AB=6,G是BC的中点将△ABG沿AG折叠至△AFG处延长GF交DC于点E,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
C
知识点二:正方形的性质
C
学以致用
6.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .
√17
知识点二:正方形的性质
思维导图
正方形的性质
矩形的性质
菱形的性质
平行四边形的性质
同时包含
包含
包含
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第59页练习1、2两题以及习题18.2第13题;
2.《导学测评》;
作业布置
1.定义:两组对边分别平行;
2.两组对边分别相等.
平行四边形的性质
边:
对角线:
角:
对角相等,邻角互补.
对角线互相平分
平行四边形是
特殊的四边形,具有
四边形的一切性质
问题引入
矩形的性质
边:
对角线:
角:
矩形是特殊的平
行四边形,具有平
行四边形的一切性质
复习引入
菱形的性质
边:
对角线:
角:
菱形是特殊的平
行四边形,具有平
行四边形的一切性质
问题引入
正方形*自我介绍
在四边形的大家庭中,我有四个兄弟.
老大是平行四边形,它性格温和;
老二是菱形,它活泼可爱;
老三是矩形,它稳重大方,江湖上人称长方形;
我就是正方形老四,我集三位大哥的优点于一身,人见人爱.
人教版八年级数学下册
第十八章 平行四边形
18.2 特殊的平行四边形
2.3 正方形(1)
——正方形及其性质
1.知道正方形与平行四边形、矩形、菱形的关系.
2.能从边、内角、对角线三个方面掌握正方形的所有性质.
重点:正方形的性质.
难点:正方形的性质在几何问题中的运用.
学习目标
重点难点
知识点一:正方形的定义
新知探究
矩形
邻边
相等
有一组邻边相等的矩形是正方形
正方形
■正方形是特殊的矩形▆
知识点一:正方形的定义
新知探究
正方形
菱形
正方形
有一个角是直角
■正方形是特殊的菱形◆
有一个角是直角的菱形是正方形
新知归纳
?有一组邻边相等的矩形是正方形;
?有一个角是直角的菱形是正方形;
?有一组邻边相等并且有一个角是直角的平行四边形是正方形.
知识点一:正方形的定义
学以致用
1.下面四个定义中不正确的是( )
A.有一个角是直角的平行四边形叫做矩形
B.有一组邻边相等的四边形叫做菱形
C.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
D.有一组邻边相等的平行四边形叫做菱形
B
知识点一:正方形的定义
2.已知在四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90° B.AB=CD C.AD=BC D.BC=CD
3.下列说法错误的是( )
A.正方形是平行四边形 B.正方形是菱形
C.正方形是矩形 D.菱形和矩形都是正方形
D
学以致用
知识点一:正方形的定义
D
归纳总结
知识点一:正方形的定义
平行四边形、矩形、菱形、正方形的关系
平行四边形
矩形
菱形
正方形
新知探究
?探究:正方形不仅是特殊的平行四边形而且是特殊的矩形、特殊的菱形,它具有哪些性质呢?
知识点二:正方形的性质
新知归纳
知识点二:正方形的性质
四条边都相等,对边平行.
正方形
的性质
边:
对角线:
角:
四个角都是直角.
对角线相等且互相垂直平分,而且每条对角线平分没有组对角.
典例讲评
例1 如图,已知点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF. 求证:DE=BE.
知识点二:正方形的性质
证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=∠BAD=90°.
∴∠BAE+∠EAD=90°.
∴EA⊥AF, ∴∠BAE+∠FAB=90°.
∴∠EAD=∠FAB.
∴△ABF≌△ADE. ∴DE=BF.
互动探究? 正方形的性质
1.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD= 度.
合作探究
知识点二:正方形的性质
22.5
互动探究? 正方形的性质
2.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF.
(2)若∠ABE=55°,求∠EGC的大小.
合作探究
知识点二:正方形的性质
归纳总结
知识点二:正方形的性质
通过证明三角形全等得到边和角相等,再进一步得到平行或垂直,是有关正方形中证边或角相等的最常用的方法,而正方形的四条边相等,四个角都是直角为证明三角形全等提供了条件.
学以致用
1. 正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.四条边相等
C.对角线相等 D.对角线互相平分
2.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.
若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4 C.5 D.6
B
B
知识点二:正方形的性质
学以致用
3.把图①中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图②、图③所示的正方形,则图①中菱形的面积为 .
12
知识点二:正方形的性质
学以致用
4.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
5.如图,正方形ABCD中,AB=6,G是BC的中点将△ABG沿AG折叠至△AFG处延长GF交DC于点E,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
C
知识点二:正方形的性质
C
学以致用
6.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为 .
√17
知识点二:正方形的性质
思维导图
正方形的性质
矩形的性质
菱形的性质
平行四边形的性质
同时包含
包含
包含
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第59页练习1、2两题以及习题18.2第13题;
2.《导学测评》;
作业布置
