人教版八年级数学下册课件:18.2特殊的平行四边形—2.3正方形(2)(共30张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2特殊的平行四边形—2.3正方形(2)(共30张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 449.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览









文档简介
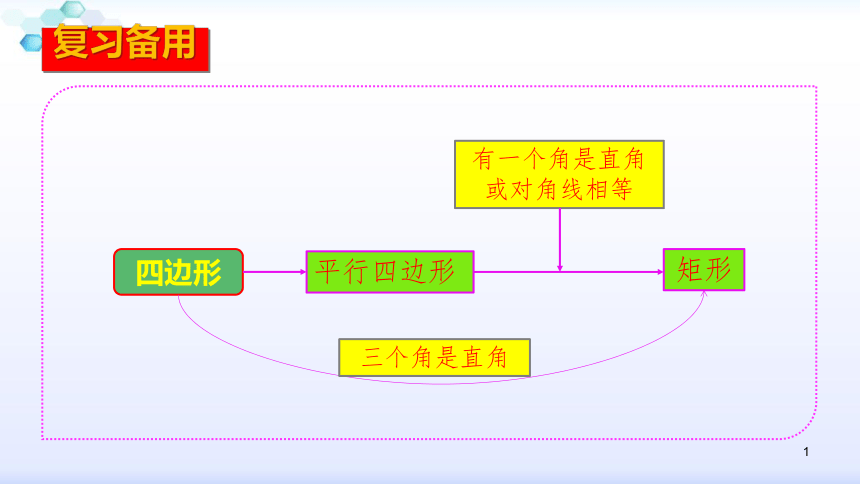
复习备用
四边形
矩形
有一个角是直角或对角线相等
平行四边形
三个角是直角
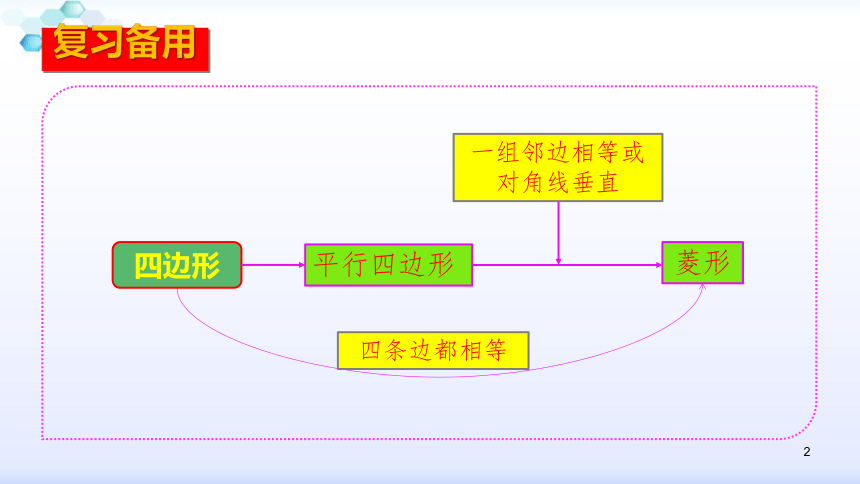
复习备用
四边形
菱形
一组邻边相等或对角线垂直
平行四边形
四条边都相等
人教版八年级数学下册
第十八章 平行四边形
18.2 特殊的平行四边形
2.3 正方形(2)
——正方形的判定
1.知道正方形、菱形、矩形、平行四边形之间的
关系.
2.掌握正方形不同的判定方法,能根据已知条件选择正确的方法判定正方形.
3.能利用特殊平行四边形的性质与判定解决相关的几何问题.
4.探究正方形的轴对称性,及其与等腰直角三
角形的关系.
重点:正方形的判定方法.
难点:综合运用特殊平行四边形的性质与判定.
学习目标
重点难点
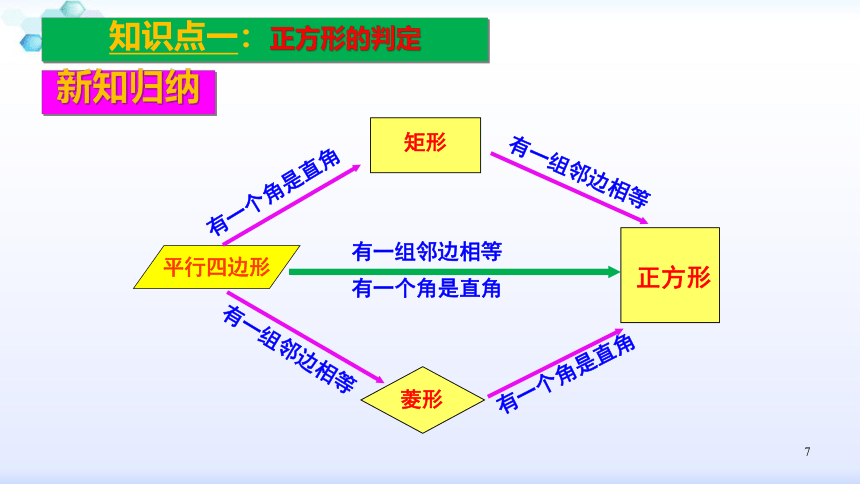
知识点一:正方形的判定
新知探究
?思考:正方形有哪些性质?如何判定一个四边形是正方形?把它们写出来,并和同学交流一下,然后证明其中的一些结论.
知识点一:正方形的判定
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.
正方形的性质=
新知探究
新知归纳
知识点一:正方形的判定
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
新知归纳
知识点一:正方形的判定
判定一个四边形是正方形,就要判定它既是矩形,又是菱形.具体判定方法如下:
?对角线互相垂直的矩形是正方形;
?对角线相等的菱形是正方形;
?对角线互相垂直且相等的平行四边形是正方形;
?有一个角是直角的菱形是正方形
?有一组邻边相等的矩形是正方形
典例讲评
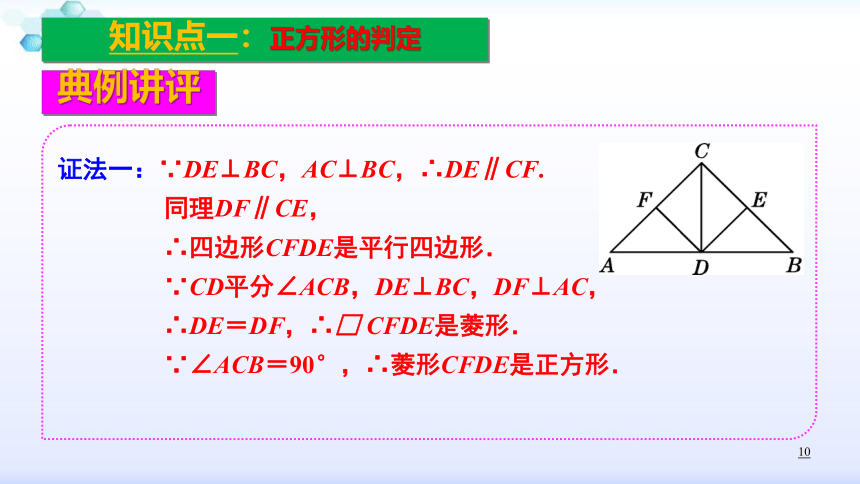
例1 如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F. 求证:四边形CFDE是正方形.
知识点一:正方形的判定
证法一:∵DE⊥BC,DF⊥AC
∴∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.
典例讲评
证法一:∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE,
∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴□ CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
知识点一:正方形的判定
新知归纳
知识点一:正方形的判定
证明条件中不含对角线的四边形是正方形的四种方法:
方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直角”;
方法3:证:“矩形+一组邻边相等”;
方法4:证:“菱形+一个直角”.
合作探究
知识点一:正方形的判定
互动探究? 正方形的判定与证明
1.下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形.
2.两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
D
D
合作探究
知识点一:正方形的判定
互动探究? 正方形的判定与证明
3.在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥AC,DF∥AB,连接EF,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形;
②如果EF⊥AD,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
B
合作探究
知识点一:正方形的判定
互动探究? 正方形的判定与证明
4.如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE
(2)判断△CEF的形状,并说明理由.
新知探究
知识点二:正方形的对称性
O
A
B
C
D
(A)
(B)
(C)
(D)
正方形的对称性:
正方形是中心对称图形,对称中心为点O;
又是轴对称图形,有四条对称轴.
典例讲评
例2 如图,点E在正方形ABCD的对角线AC上,且EC
=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. a2 B. a2
C. a2 D. a2
知识点二:正方形的对称性
D
学以致用
1. 如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为________.
2.将五个边长都为2 cm的正方形按如图所示方式摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
知识点二:正方形的对称性
13cm
B
学以致用
3.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J,则图中阴影部分的面积等于( )
A.1 B. C. D.
B
知识点二:正方形的对称性
学以致用
4.如图,点E在正方形ABCD的对角线AC上,E为AC的中点,Rt△FEG的两条直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD的边长为a,则阴影部分即四边形EMCN的面积为( )
B
知识点二:正方形的对称性
A. a2 B. a2 C. a2 D. a2
新知探究
知识点三:平行四边形与特殊平行四边形之间的关系
5种识别方法
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
四条边相等
三个角是直角
典例讲评
例3 如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
知识点三:平行四边形与特殊平行四边形之间的关系
证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO,
∵EA=EC,
∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
典例讲评
例3 如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD是正方形.
知识点三:平行四边形与特殊平行四边形之间的关系
(2)∵∠ADO=∠EAD+∠AED,∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.
归纳总结
证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
知识点三:平行四边形与特殊平行四边形之间的关系
学以致用
1.如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件_________,使四边形ABCD是正方形.
知识点三:平行四边形与特殊平行四边形之间的关系
∠BAD=90°
2.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
D
学以致用
3.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形
②存在无数个四边形MNPQ是矩形
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MMPQ是正方形
所有正确结论的序号是 .
①②③
知识点三:平行四边形与特殊平行四边形之间的关系
学以致用
4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使□ABCD为正方形(如图),现有下列四种选法,
你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
B
知识点三:平行四边形与特殊平行四边形之间的关系
学以致用
5.四边形ABCD的对角线AC和BD相交于点O,假设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;
④四边形ABCD为矩形;⑤四边形ABCD为菱形;⑥四边形ABCD为正方形则下列推理不成立的是( )
A.①④→⑥ B.①③→⑤
C.①②→⑥ D.②③→④
C
知识点三:平行四边形与特殊平行四边形之间的关系
思维导图
四边形
矩形
正方形
菱形
平行四边形
满足一个条件
满足一个条件
满足一个条件
同时满足
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第60页练习第3题以及习题18.2第13-17题;
2.《导学测评》;
作业布置
四边形
矩形
有一个角是直角或对角线相等
平行四边形
三个角是直角
复习备用
四边形
菱形
一组邻边相等或对角线垂直
平行四边形
四条边都相等
人教版八年级数学下册
第十八章 平行四边形
18.2 特殊的平行四边形
2.3 正方形(2)
——正方形的判定
1.知道正方形、菱形、矩形、平行四边形之间的
关系.
2.掌握正方形不同的判定方法,能根据已知条件选择正确的方法判定正方形.
3.能利用特殊平行四边形的性质与判定解决相关的几何问题.
4.探究正方形的轴对称性,及其与等腰直角三
角形的关系.
重点:正方形的判定方法.
难点:综合运用特殊平行四边形的性质与判定.
学习目标
重点难点
知识点一:正方形的判定
新知探究
?思考:正方形有哪些性质?如何判定一个四边形是正方形?把它们写出来,并和同学交流一下,然后证明其中的一些结论.
知识点一:正方形的判定
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.
正方形的性质=
新知探究
新知归纳
知识点一:正方形的判定
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
新知归纳
知识点一:正方形的判定
判定一个四边形是正方形,就要判定它既是矩形,又是菱形.具体判定方法如下:
?对角线互相垂直的矩形是正方形;
?对角线相等的菱形是正方形;
?对角线互相垂直且相等的平行四边形是正方形;
?有一个角是直角的菱形是正方形
?有一组邻边相等的矩形是正方形
典例讲评
例1 如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F. 求证:四边形CFDE是正方形.
知识点一:正方形的判定
证法一:∵DE⊥BC,DF⊥AC
∴∠ECF=∠CFD=∠CED=90°,
∴四边形CFDE是矩形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴矩形CFDE是正方形.
典例讲评
证法一:∵DE⊥BC,AC⊥BC,∴DE∥CF.
同理DF∥CE,
∴四边形CFDE是平行四边形.
∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,∴□ CFDE是菱形.
∵∠ACB=90°,∴菱形CFDE是正方形.
知识点一:正方形的判定
新知归纳
知识点一:正方形的判定
证明条件中不含对角线的四边形是正方形的四种方法:
方法1:证:“四边形+四边相等+四个直角”;
方法2:证:“平行四边形+一组邻边相等+一个直角”;
方法3:证:“矩形+一组邻边相等”;
方法4:证:“菱形+一个直角”.
合作探究
知识点一:正方形的判定
互动探究? 正方形的判定与证明
1.下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形.
2.两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
D
D
合作探究
知识点一:正方形的判定
互动探究? 正方形的判定与证明
3.在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥AC,DF∥AB,连接EF,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形;
②如果EF⊥AD,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
B
合作探究
知识点一:正方形的判定
互动探究? 正方形的判定与证明
4.如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE
(2)判断△CEF的形状,并说明理由.
新知探究
知识点二:正方形的对称性
O
A
B
C
D
(A)
(B)
(C)
(D)
正方形的对称性:
正方形是中心对称图形,对称中心为点O;
又是轴对称图形,有四条对称轴.
典例讲评
例2 如图,点E在正方形ABCD的对角线AC上,且EC
=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. a2 B. a2
C. a2 D. a2
知识点二:正方形的对称性
D
学以致用
1. 如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为________.
2.将五个边长都为2 cm的正方形按如图所示方式摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
知识点二:正方形的对称性
13cm
B
学以致用
3.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J,则图中阴影部分的面积等于( )
A.1 B. C. D.
B
知识点二:正方形的对称性
学以致用
4.如图,点E在正方形ABCD的对角线AC上,E为AC的中点,Rt△FEG的两条直角边EF,EG分别交BC,DC于点M,N.若正方形ABCD的边长为a,则阴影部分即四边形EMCN的面积为( )
B
知识点二:正方形的对称性
A. a2 B. a2 C. a2 D. a2
新知探究
知识点三:平行四边形与特殊平行四边形之间的关系
5种识别方法
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
四条边相等
三个角是直角
典例讲评
例3 如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.
(1)求证:四边形ABCD是菱形;
知识点三:平行四边形与特殊平行四边形之间的关系
证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO,
∵EA=EC,
∴EO⊥AC,即BD⊥AC,
∴四边形ABCD是菱形.
典例讲评
例3 如图,已知在□ABCD中,对角线AC,BD交于点O,E是BD的延长线上的点,且EA=EC.(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD是正方形.
知识点三:平行四边形与特殊平行四边形之间的关系
(2)∵∠ADO=∠EAD+∠AED,∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD是菱形,∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD是正方形.
归纳总结
证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
知识点三:平行四边形与特殊平行四边形之间的关系
学以致用
1.如图,在菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件_________,使四边形ABCD是正方形.
知识点三:平行四边形与特殊平行四边形之间的关系
∠BAD=90°
2.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
D
学以致用
3.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形
②存在无数个四边形MNPQ是矩形
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MMPQ是正方形
所有正确结论的序号是 .
①②③
知识点三:平行四边形与特殊平行四边形之间的关系
学以致用
4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使□ABCD为正方形(如图),现有下列四种选法,
你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
B
知识点三:平行四边形与特殊平行四边形之间的关系
学以致用
5.四边形ABCD的对角线AC和BD相交于点O,假设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;
④四边形ABCD为矩形;⑤四边形ABCD为菱形;⑥四边形ABCD为正方形则下列推理不成立的是( )
A.①④→⑥ B.①③→⑤
C.①②→⑥ D.②③→④
C
知识点三:平行四边形与特殊平行四边形之间的关系
思维导图
四边形
矩形
正方形
菱形
平行四边形
满足一个条件
满足一个条件
满足一个条件
同时满足
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第60页练习第3题以及习题18.2第13-17题;
2.《导学测评》;
作业布置
