人教版八年级数学下册课件:18.2特殊的平行四边形—2.3正方形(3)(共21张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2特殊的平行四边形—2.3正方形(3)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 344.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览





文档简介
复习备用
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
正方形性质
面积公式
边
角
对角线
对称性
对边平行,四条边都相等
四个角都是直角
两条对角线相等且互相垂直平分,每条对角线平分每一组对角
正方形是轴对称图形,有四条对称轴
①正方形的面积
=边长的平分;
②正方形的面积
=对角线乘积的一半.
复习备用
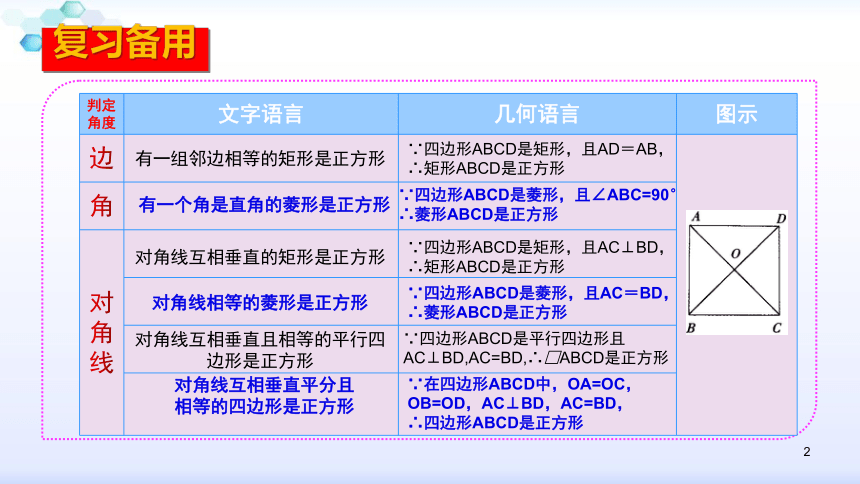
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判定角度
文字语言
几何语言
图示
边
角
对
角
线
有一组邻边相等的矩形是正方形
∵四边形ABCD是矩形,且AD=AB,
∴矩形ABCD是正方形
有一个角是直角的菱形是正方形
对角线互相垂直的矩形是正方形
∵四边形ABCD是菱形,且∠ABC=90°
∴菱形ABCD是正方形
∵四边形ABCD是矩形,且AC⊥BD,
∴矩形ABCD是正方形
∵四边形ABCD是菱形,且AC=BD,
∴菱形ABCD是正方形
∵四边形ABCD是平行四边形且AC⊥BD,AC=BD,∴□ABCD是正方形
∵在四边形ABCD中,OA=OC,OB=OD,AC⊥BD,AC=BD,
∴四边形ABCD是正方形
对角线相等的菱形是正方形
对角线互相垂直且相等的平行四边形是正方形
对角线互相垂直平分且
相等的四边形是正方形
人教版八年级数学下册
第十八章 平行四边形
18.2 特殊的平行四边形
2.3 正方形(3)
——正方形的性质与判定的综合应用
正方形的判定方法:正方形既是矩形,又是菱形,它具有矩形、菱形的所有性质;判定一个四边形是正方形,只需保证它既是矩形又是菱形即可,即:证明矩形是菱形,菱形是矩形.
正方形的判定方法
典例讲评
例1 如图,正方形ABCD的边长为3,E,F分别是AB,BC
边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
2)当AE=1时,求EF的长.
知识点一:与正方形有关的旋转、动点问题
知识点一:与正方形有关的旋转、动点问题
学以致用
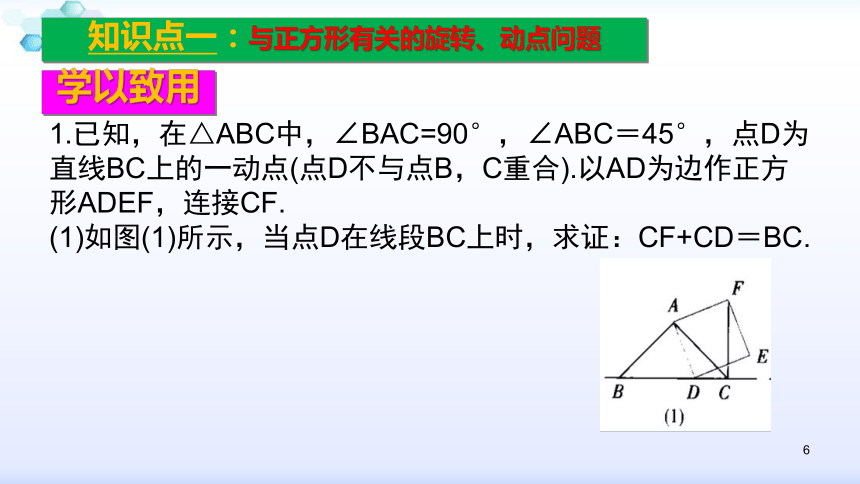
1.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上的一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图(1)所示,当点D在线段BC上时,求证:CF+CD=BC.
知识点一:与正方形有关的旋转、动点问题
学以致用
1.(2)如图(2)所示,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的等量关系.
知识点一:与正方形有关的旋转、动点问题
学以致用
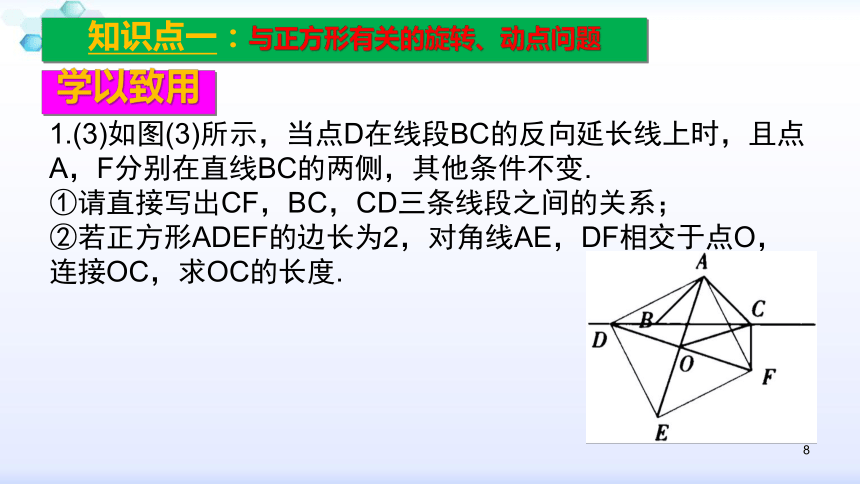
1.(3)如图(3)所示,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变.
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC,求OC的长度.
知识点一:与正方形有关的旋转、动点问题
学以致用
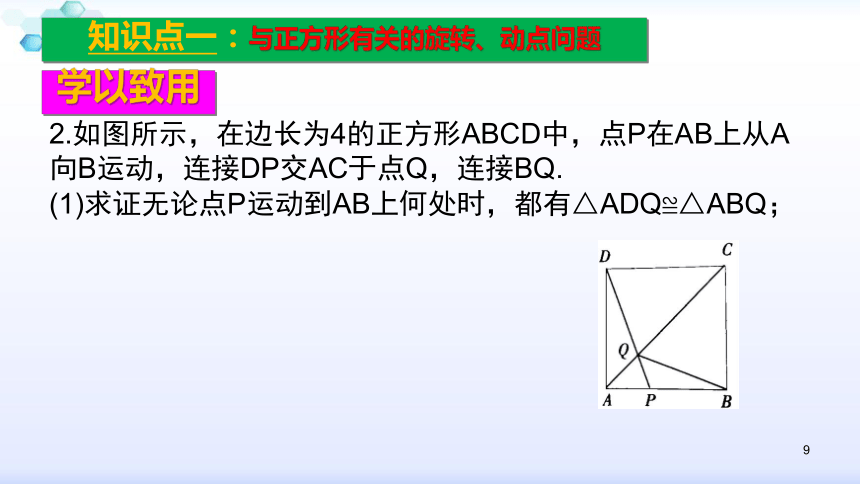
2.如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ.
(1)求证无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
知识点一:与正方形有关的旋转、动点问题
学以致用
2.如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ.
(2)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形?
典例讲评
例2 如图,在四边形ABCD中,点E是线段AD上任意点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
1)求证:四边形EGFH是平行四边形;
知识点二:正方形性质和判定的综合应用
典例讲评
例2 如图,在四边形ABCD中,点E是线段AD上任意点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
2)EF和BC满足什么关系时,平行四边形EGFH是正方形?
知识点二:正方形性质和判定的综合应用
学以致用
1.如图所示,在△ABC中,D是BC边上的点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
知识点二:正方形性质和判定的综合应用
学以致用
1.如图所示,在△ABC中,D是BC边上的点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(2)如果AB=AC,试猜想四边形ADCF
的形状并证明你的结论;
知识点二:正方形性质和判定的综合应用
学以致用
1.如图所示,在△ABC中,D是BC边上的点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(3)△ABC满足什么条件时,四边形ADCF
为正方形?并证明你的结论.
知识点二:正方形性质和判定的综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(1)探究OE与OF的数量关系并加以证明;
知识点三:正方形与特殊平行四边形综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(2)连接BE,当点O在边AC上运动时,四边形BCFE能否为菱形?若能,请证明;若不能,请说明理由;
知识点三:正方形与特殊平行四边形综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(3)连接AE,AF,当点O在AC上运动到什么位置时,四边形AECF是矩形,请说明理由;
知识点三:正方形与特殊平行四边形综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(4)在(3)的条件下,△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
知识点三:正方形与特殊平行四边形综合应用
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.《能力》;
2.《导学测评》;
作业布置
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
正方形性质
面积公式
边
角
对角线
对称性
对边平行,四条边都相等
四个角都是直角
两条对角线相等且互相垂直平分,每条对角线平分每一组对角
正方形是轴对称图形,有四条对称轴
①正方形的面积
=边长的平分;
②正方形的面积
=对角线乘积的一半.
复习备用
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判定角度
文字语言
几何语言
图示
边
角
对
角
线
有一组邻边相等的矩形是正方形
∵四边形ABCD是矩形,且AD=AB,
∴矩形ABCD是正方形
有一个角是直角的菱形是正方形
对角线互相垂直的矩形是正方形
∵四边形ABCD是菱形,且∠ABC=90°
∴菱形ABCD是正方形
∵四边形ABCD是矩形,且AC⊥BD,
∴矩形ABCD是正方形
∵四边形ABCD是菱形,且AC=BD,
∴菱形ABCD是正方形
∵四边形ABCD是平行四边形且AC⊥BD,AC=BD,∴□ABCD是正方形
∵在四边形ABCD中,OA=OC,OB=OD,AC⊥BD,AC=BD,
∴四边形ABCD是正方形
对角线相等的菱形是正方形
对角线互相垂直且相等的平行四边形是正方形
对角线互相垂直平分且
相等的四边形是正方形
人教版八年级数学下册
第十八章 平行四边形
18.2 特殊的平行四边形
2.3 正方形(3)
——正方形的性质与判定的综合应用
正方形的判定方法:正方形既是矩形,又是菱形,它具有矩形、菱形的所有性质;判定一个四边形是正方形,只需保证它既是矩形又是菱形即可,即:证明矩形是菱形,菱形是矩形.
正方形的判定方法
典例讲评
例1 如图,正方形ABCD的边长为3,E,F分别是AB,BC
边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
2)当AE=1时,求EF的长.
知识点一:与正方形有关的旋转、动点问题
知识点一:与正方形有关的旋转、动点问题
学以致用
1.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上的一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图(1)所示,当点D在线段BC上时,求证:CF+CD=BC.
知识点一:与正方形有关的旋转、动点问题
学以致用
1.(2)如图(2)所示,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的等量关系.
知识点一:与正方形有关的旋转、动点问题
学以致用
1.(3)如图(3)所示,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变.
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC,求OC的长度.
知识点一:与正方形有关的旋转、动点问题
学以致用
2.如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ.
(1)求证无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
知识点一:与正方形有关的旋转、动点问题
学以致用
2.如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q,连接BQ.
(2)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形?
典例讲评
例2 如图,在四边形ABCD中,点E是线段AD上任意点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
1)求证:四边形EGFH是平行四边形;
知识点二:正方形性质和判定的综合应用
典例讲评
例2 如图,在四边形ABCD中,点E是线段AD上任意点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.
2)EF和BC满足什么关系时,平行四边形EGFH是正方形?
知识点二:正方形性质和判定的综合应用
学以致用
1.如图所示,在△ABC中,D是BC边上的点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
知识点二:正方形性质和判定的综合应用
学以致用
1.如图所示,在△ABC中,D是BC边上的点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(2)如果AB=AC,试猜想四边形ADCF
的形状并证明你的结论;
知识点二:正方形性质和判定的综合应用
学以致用
1.如图所示,在△ABC中,D是BC边上的点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(3)△ABC满足什么条件时,四边形ADCF
为正方形?并证明你的结论.
知识点二:正方形性质和判定的综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(1)探究OE与OF的数量关系并加以证明;
知识点三:正方形与特殊平行四边形综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(2)连接BE,当点O在边AC上运动时,四边形BCFE能否为菱形?若能,请证明;若不能,请说明理由;
知识点三:正方形与特殊平行四边形综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(3)连接AE,AF,当点O在AC上运动到什么位置时,四边形AECF是矩形,请说明理由;
知识点三:正方形与特殊平行四边形综合应用
典例讲评
例3 如图,在△ABC中,点O是AC边上一个动点,过点O
作直线MN∥BC,设MN交∠BCA的平分线于点E交△BCA的外角∠ACD的平分线于点F.
(4)在(3)的条件下,△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
知识点三:正方形与特殊平行四边形综合应用
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.《能力》;
2.《导学测评》;
作业布置
