人教版八年级下册 19.3《课题学习:选择方案(调水问题)》课件(共19张PPT)
文档属性
| 名称 | 人教版八年级下册 19.3《课题学习:选择方案(调水问题)》课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览





文档简介
天祝三中 张成山
y = kx+b
x
y
我国的南水北调工程
1、某车从九集粮站调运20吨的小麦到80千米外的枣阳面粉厂,这辆车的调运量为 。
(友情提示:调运量=质量×运程)
2、枣阳面粉厂现急需40吨的小麦用于生产面粉,现从九集购买了(x+2)吨,则还需要从其它地方购买 吨才能满足需要?
活动一:知识准备
20×80=1600
40-(x+2)=38-x
活动二:引入新课
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小.
A
B
甲
乙
活动三:新课讲解
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小.
A
B
甲
乙
14万吨
14万吨
X
14-x
15-x
13-(14-x)=x-1
15万吨
13万吨
总计
B
A
总计
乙
甲
X
14-x
14
15-x
x-1
14
15
13
28
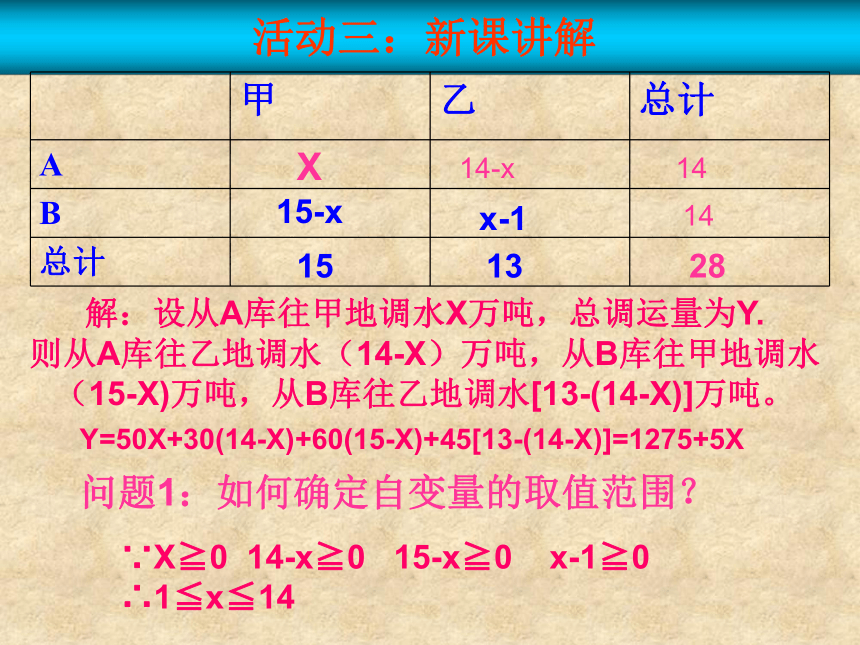
活动三:新课讲解
总计
B
A
总计
乙
甲
X
14-x
14
15-x
x-1
14
15
13
28
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=1275+5X
问题1:如何确定自变量的取值范围?
∵X≧0 14-x≧0 15-x≧0 x-1≧0
∴1≦x≦14
活动三:新课讲解
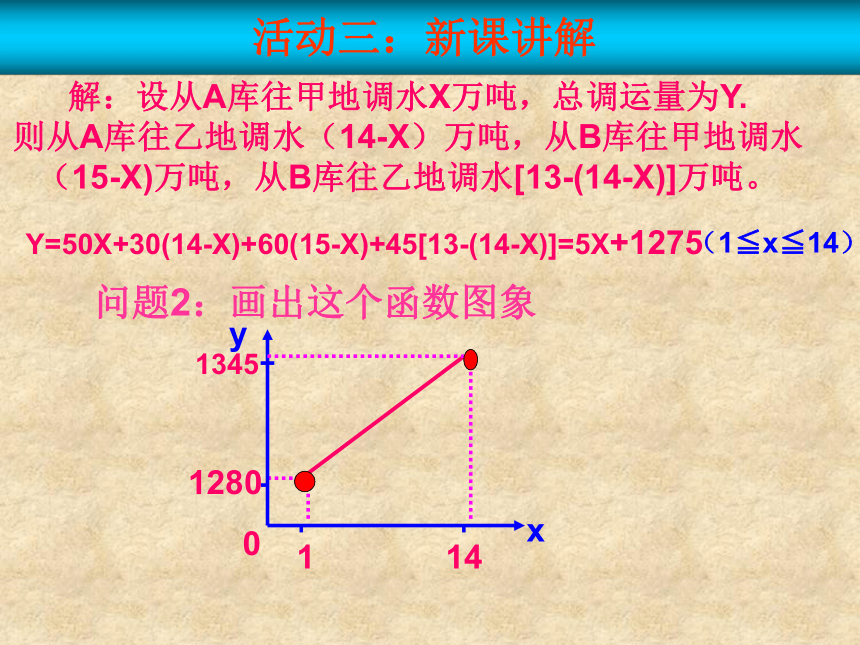
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=5X+1275
问题2:画出这个函数图象
(1≦x≦14)
1345
1280
14
1
0
x
y
活动三:新课讲解
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=5X+1275
问题3:结合函数解析式及图象说明水的最佳调运方案。水的最小调运量为多少?
(1≦x≦14)
∵k=5>0 y随x的增大而增大
∴当x取最小值1时,Y有最小值1280
所以,从A库往甲地调水1万吨,从A库往乙地调水13万吨,从B库往甲地调水14万吨,从B库往乙地调水0万吨,可使水的调运量最小.
活动四:合作交流
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=5X+1275
(1≦x≦14)
∵k=5>0 y随x的增大而增大
∴当x=1时,Y有最小值1280
所以,从A库往甲地调水1万吨,从A库往乙地调水13万吨,从B库往甲地调水14万吨,从B库往乙地调水0万吨,可使水的调运量最小.
问题4:如果设其他水量(例如从B水库调往乙地的水量)为x万吨,能得到同样的最佳方案吗?
例1 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨,D乡需要肥料260吨,怎样调运总运费最少?
A城有肥料200吨
B城有肥料300吨
C乡需要肥料240吨
D乡需要肥料260吨
每吨20元
每吨24元
每吨25元
每吨15元
思考:影响总运费的变量有哪些?由A、B城分别运往C、D乡的 肥料量共有几个量?这些量之间有什么关系?
活动五:巩固提高
例1 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨,D乡需要肥料260吨,怎样调运总运费最少?
500吨
260吨
240吨
总计
300吨
B
200吨
x吨
A
总计
D
C
收地
运地
(200-x)吨
(240-x)吨
(60+x)吨
活动五:巩固提高
解:设从A城调往C乡的化肥为x吨 ,总运费为y元则
从A城调往D乡的化肥为 吨
从B城调往C乡的化肥为 吨
从B城调往D乡的化肥为 吨
所以y=20x+25(200-x)+15(240-x)+24(x+60)
(200- x)
(240-x)
(X+60)
(1)化简这个函数,并指出其中自变量x的取值应有什么
限制条件?
y=4x+10040
(0≤x≤200)
活动五:巩固提高
10840
10040
y(元)
200
0
x(吨)
o
y
x
·
10040
·
10840
·
200
·
·
y=4x+10040 (0≤x≤200)
从图象观测:
(2)
答:一次函数 y=4x+10040的值 y随x 的增大而增大,所以当x=0时y 有最小值,最小值为4×0+10040=10040,所以这次运化肥的方案应从A城调往C乡0吨,调往D乡200吨;从B城调往C乡240吨,调往D乡60吨。
(3)如果设其它运量(例如从B城调往C乡的化肥为x吨,能得到同样的最佳方案吗?
试一试 你也一定能行
A市和B各有机床12台和6台,现运往C市10台,D市8台,若从A市运一台到C市,D市各需要4万元和8万元,从B市运一台到C市,D市各需3万元和5万元。
(1)设B市运往C市x台,求总费用y关于x的函数关系式;
(2)若总费用不超过95万元,问共有多少种调运方法?
(3)求总费用最低的调运方法,最低费用是多少万元?
活动六:达标练习
解决含有多个变量的问题时,可以分析这些变量间的关系,选取其中某个变量作为自变量,然后根据问题中的条件寻求可以反映实际问题的函数.
实际问题
数学问题
数学问题的解
建立函数
解函数问题
活动七:课堂小结
通过这节课的学习,你有什么收获?谈谈吧!
(1)解决含有多个变量的问题时,可以采用列表等辅助方式分析这些变量之间的关系,从中选取有代表性的变量设为自变量x,进一步表达出其它的变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型。
(2) 对于实际问题,一般自变量都有它的取值范围,应充分利用函数增减性判断最大值或最小值。这种最值问题往往用来解决“成本最省”或“利润最大”等方面的问题。
你知道了吗?
活动八:课后 作业
课本139页第12题
y = kx+b
x
y
y = kx+b
x
y
我国的南水北调工程
1、某车从九集粮站调运20吨的小麦到80千米外的枣阳面粉厂,这辆车的调运量为 。
(友情提示:调运量=质量×运程)
2、枣阳面粉厂现急需40吨的小麦用于生产面粉,现从九集购买了(x+2)吨,则还需要从其它地方购买 吨才能满足需要?
活动一:知识准备
20×80=1600
40-(x+2)=38-x
活动二:引入新课
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小.
A
B
甲
乙
活动三:新课讲解
从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A、B两水库各可调出水14万吨.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.设计一个调运方案使水的调运量(单位:万吨·千米)尽可能小.
A
B
甲
乙
14万吨
14万吨
X
14-x
15-x
13-(14-x)=x-1
15万吨
13万吨
总计
B
A
总计
乙
甲
X
14-x
14
15-x
x-1
14
15
13
28
活动三:新课讲解
总计
B
A
总计
乙
甲
X
14-x
14
15-x
x-1
14
15
13
28
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=1275+5X
问题1:如何确定自变量的取值范围?
∵X≧0 14-x≧0 15-x≧0 x-1≧0
∴1≦x≦14
活动三:新课讲解
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=5X+1275
问题2:画出这个函数图象
(1≦x≦14)
1345
1280
14
1
0
x
y
活动三:新课讲解
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=5X+1275
问题3:结合函数解析式及图象说明水的最佳调运方案。水的最小调运量为多少?
(1≦x≦14)
∵k=5>0 y随x的增大而增大
∴当x取最小值1时,Y有最小值1280
所以,从A库往甲地调水1万吨,从A库往乙地调水13万吨,从B库往甲地调水14万吨,从B库往乙地调水0万吨,可使水的调运量最小.
活动四:合作交流
解:设从A库往甲地调水X万吨,总调运量为Y.
则从A库往乙地调水(14-X)万吨,从B库往甲地调水(15-X)万吨,从B库往乙地调水[13-(14-X)]万吨。
Y=50X+30(14-X)+60(15-X)+45[13-(14-X)]=5X+1275
(1≦x≦14)
∵k=5>0 y随x的增大而增大
∴当x=1时,Y有最小值1280
所以,从A库往甲地调水1万吨,从A库往乙地调水13万吨,从B库往甲地调水14万吨,从B库往乙地调水0万吨,可使水的调运量最小.
问题4:如果设其他水量(例如从B水库调往乙地的水量)为x万吨,能得到同样的最佳方案吗?
例1 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨,D乡需要肥料260吨,怎样调运总运费最少?
A城有肥料200吨
B城有肥料300吨
C乡需要肥料240吨
D乡需要肥料260吨
每吨20元
每吨24元
每吨25元
每吨15元
思考:影响总运费的变量有哪些?由A、B城分别运往C、D乡的 肥料量共有几个量?这些量之间有什么关系?
活动五:巩固提高
例1 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨,D乡需要肥料260吨,怎样调运总运费最少?
500吨
260吨
240吨
总计
300吨
B
200吨
x吨
A
总计
D
C
收地
运地
(200-x)吨
(240-x)吨
(60+x)吨
活动五:巩固提高
解:设从A城调往C乡的化肥为x吨 ,总运费为y元则
从A城调往D乡的化肥为 吨
从B城调往C乡的化肥为 吨
从B城调往D乡的化肥为 吨
所以y=20x+25(200-x)+15(240-x)+24(x+60)
(200- x)
(240-x)
(X+60)
(1)化简这个函数,并指出其中自变量x的取值应有什么
限制条件?
y=4x+10040
(0≤x≤200)
活动五:巩固提高
10840
10040
y(元)
200
0
x(吨)
o
y
x
·
10040
·
10840
·
200
·
·
y=4x+10040 (0≤x≤200)
从图象观测:
(2)
答:一次函数 y=4x+10040的值 y随x 的增大而增大,所以当x=0时y 有最小值,最小值为4×0+10040=10040,所以这次运化肥的方案应从A城调往C乡0吨,调往D乡200吨;从B城调往C乡240吨,调往D乡60吨。
(3)如果设其它运量(例如从B城调往C乡的化肥为x吨,能得到同样的最佳方案吗?
试一试 你也一定能行
A市和B各有机床12台和6台,现运往C市10台,D市8台,若从A市运一台到C市,D市各需要4万元和8万元,从B市运一台到C市,D市各需3万元和5万元。
(1)设B市运往C市x台,求总费用y关于x的函数关系式;
(2)若总费用不超过95万元,问共有多少种调运方法?
(3)求总费用最低的调运方法,最低费用是多少万元?
活动六:达标练习
解决含有多个变量的问题时,可以分析这些变量间的关系,选取其中某个变量作为自变量,然后根据问题中的条件寻求可以反映实际问题的函数.
实际问题
数学问题
数学问题的解
建立函数
解函数问题
活动七:课堂小结
通过这节课的学习,你有什么收获?谈谈吧!
(1)解决含有多个变量的问题时,可以采用列表等辅助方式分析这些变量之间的关系,从中选取有代表性的变量设为自变量x,进一步表达出其它的变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型。
(2) 对于实际问题,一般自变量都有它的取值范围,应充分利用函数增减性判断最大值或最小值。这种最值问题往往用来解决“成本最省”或“利润最大”等方面的问题。
你知道了吗?
活动八:课后 作业
课本139页第12题
y = kx+b
x
y
