人教版八年级下册 19.3《课题学习:选择方案》教学课件(共25张PPT)
文档属性
| 名称 | 人教版八年级下册 19.3《课题学习:选择方案》教学课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 18:34:47 | ||
图片预览




文档简介
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
19.3
课题学习
选择方案
问题一:怎样选取上网收费方式
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选择哪种方式能节省上网费?
下表给出A,B,C三种上宽带网的收费方式.
问题1
怎样选取上网收费方式?
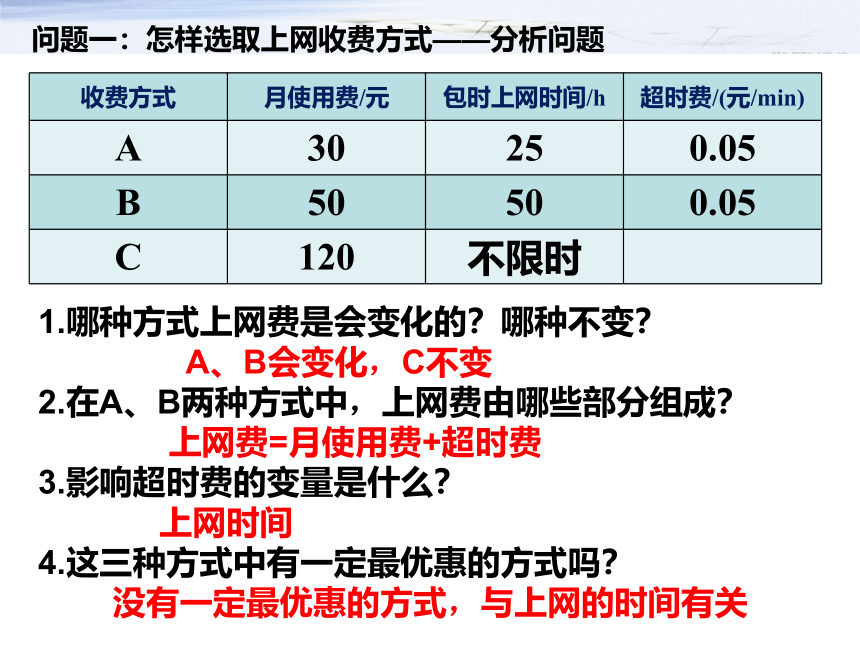
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在
x
>
0
时,考虑何时
(1)
y1
=
y2;
(2)
y1
<
y2;
(3)
y1
>
y2.
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
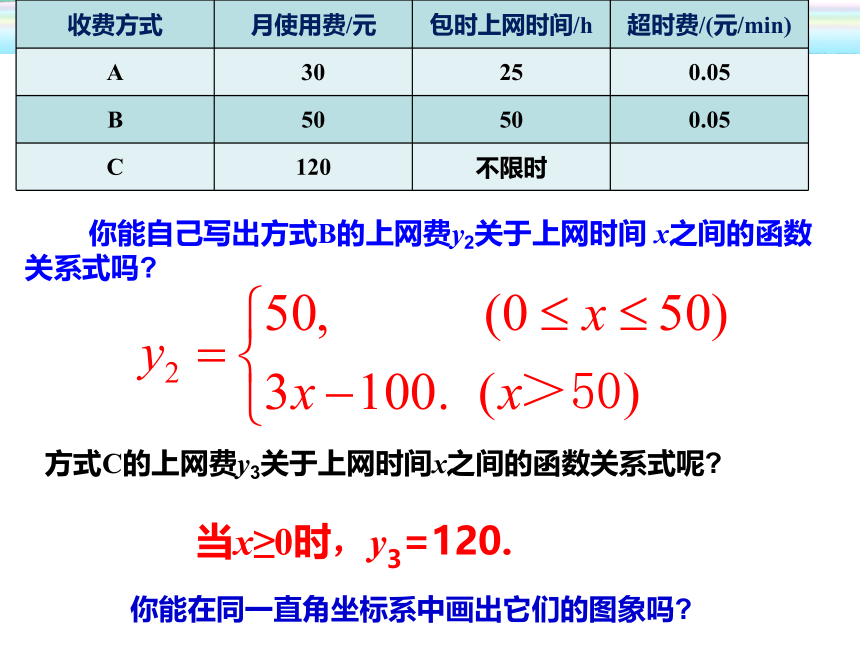
你能自己写出方式B的上网费y2关于上网时间
x之间的函数关系式吗?
方式C的上网费y3关于上网时间x之间的函数关系式呢?
你能在同一直角坐标系中画出它们的图象吗?
当x≥0时,y3=120.
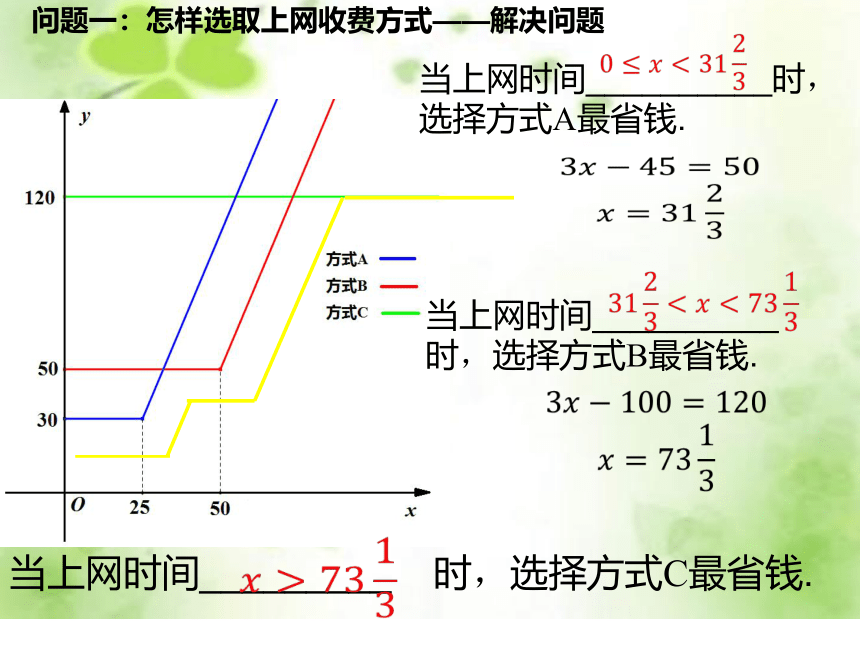
问题一:怎样选取上网收费方式——解决问题
当上网时间__________时,
选择方式A最省钱.
当上网时间__________
时,选择方式B最省钱.
当上网时间_________
时,选择方式C最省钱.
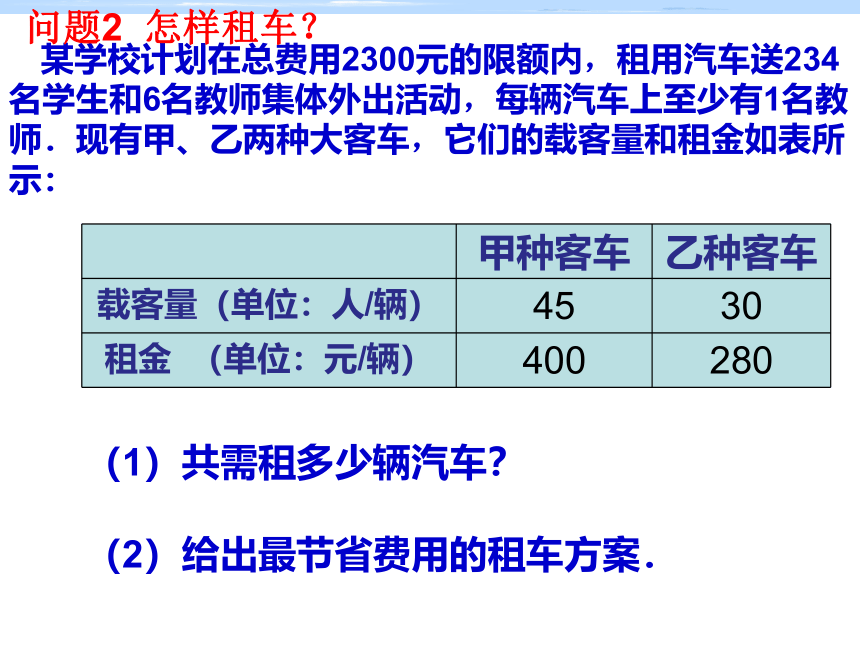
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
Zx`````x``k
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
问题2
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示
:
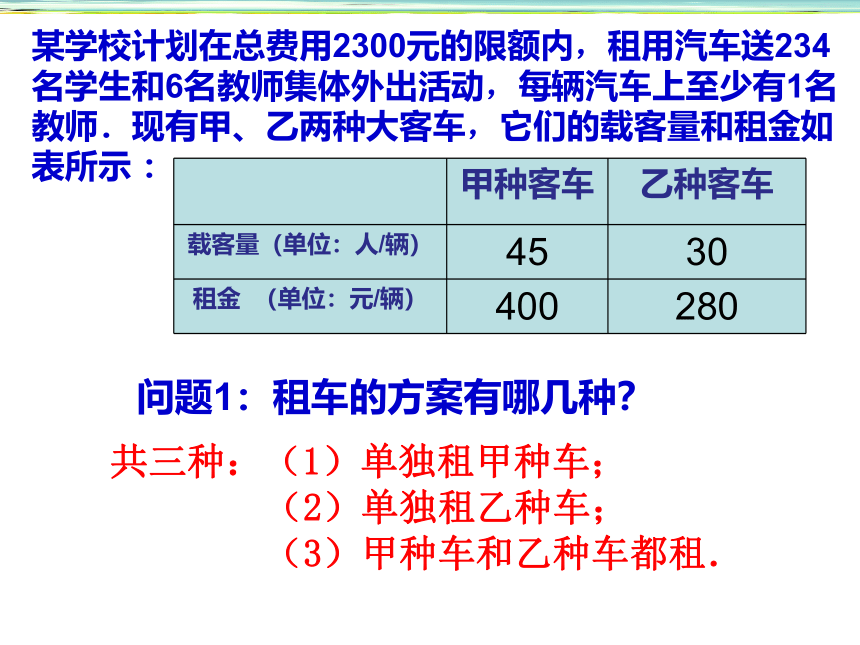
问题1:租车的方案有哪几种?
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
共三种:(1)单独租甲种车;
(2)单独租乙种车;
(3)甲种车和乙种车都租.
问题二:怎样租车——分析问题
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
问题二:怎样租车——分析问题
问题4:要使6名教师至少在每辆车上有一名,你能确定
排除哪种方案?你能确定租车的辆数吗?
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
说明了车辆总数不会超过6辆,可以排除方案2——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有
很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分5种情况;
方法2:设租甲种车x辆,确定x的范围.
(1)为使240名师生有车坐,
可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案?为节省费用应选择其中的哪种方案?
问题二:怎样租车——分析问题
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
设租用
x
辆甲种客车,则租车费用y(单位:元)是
x
的函数,即
怎样确定
x
的取值范围呢?
x
辆
(6-x)辆
问题二:怎样租车——解决问题
由函数可知
y
随
x
增大而增大,所以
x
=
4时
y
最小,所以租用4辆甲车,2辆乙车.
变式练习
1000
2000
500
1500
1000
2000
2500
x(km)
y(元)
0
y1
y2
1.某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同.
设汽车每月行驶
x
km,应付给个体车主的月租费是y1元,付给出租公司的月租费是y2
元,y1,y2
分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
当0<x<1500时,租国有的合算.
当x=1500时,租两家的费用一样.
租个体车主的车合算.
变式练习
2.某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折优惠.”若全票价为240元.
(1)设学生数为
x,甲旅行社收费为
y甲,乙旅行社收费为
y乙,分别计算两家旅行社的收费(建立表达式);
zx`````x``k
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
当x
=
4时,两家旅行社的收费一样.
当x
<
4时,甲旅行社优惠;当x
>
4时,乙旅行社优惠.
课堂小结
实际问题
函数模型
实际问题的解
函数模型的解
抽象概括
还原说明
作业布置
?
甲
乙
丙
每辆汽车能装的吨数
2
1
1.5
每吨蔬菜可获利润(元)
500
700
400
1.下表所示为装运甲、乙、丙三种蔬菜的重量及利润.某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只装一种蔬菜).
(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运乙、丙两种蔬菜的汽车各多少辆?
(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售(每种蔬菜不少于一车),如何安排装运,可使公司获得最大利润?最大利润是多少?
某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件。
(1)所获利润y元与制造甲种零件x人关系
(2)若每天所获利润不低于24000元,你认为至少要派多少名工人制造乙种零件合适?
y=6x·150+5(20-x)
·260
y=26000-400x(0≤x≤20)
解:(1)
(2)∵y≥24000
∴26000-400x≥24000
∴x≤5
∴20-x≥15
答,车间每天至少安排15人才合适。
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
最佳方案的选择
哪种灯省钱
一种节能灯的功率为10瓦(即0.01千瓦)售价为60元,一种白炽灯功率为60瓦(即0.06千瓦)售价为3元。两种灯的照明效果一样,使用寿命也相同(3000小时以上)如果电费价格为0.5元/千瓦·时,消费者选用哪种灯省钱?
费用=电费+灯的售价
设照明时间为x小时,则节能灯的总费用为
=0.5×0.01x+60
=0.5×0.06x+3
可利用解析式及图像,结合方程与不等式去说明
y
>y
1
2
y
<y
1
2
即:0.5×0.01x+60=0.5×0.06x+3
x=2280
即:0.5×0.01x+60>0.5×0.06x+3
x<2280
即:0.5×0.01x+60<0.5×0.06x+3
x>2280
答:当x=2280时选用两种灯总费用一样
当x<2280时选用白炽灯总费用省
当x>2280时选用节能灯总费用省
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
作业布置
?
甲
乙
丙
每辆汽车能装的吨数
2
1
1.5
每吨蔬菜可获利润(元)
500
700
400
3.下表所示为装运甲、乙、丙三种蔬菜的重量及利润.某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只装一种蔬菜).
(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运乙、丙两种蔬菜的汽车各多少辆?
(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售(每种蔬菜不少于一车),如何安排装运,可使公司获得最大利润?最大利润是多少?
4.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件。
(1)所获利润y元与制造甲种零件x人关系
(2)若每天所获利润不低于24000元,你认为至少要派多少名工人制造乙种零件合适?
y=6x·150+5(20-x)
·260
y=26000-400x(0≤x≤20)
解:(1)
(2)∵y≥24000
∴26000-400x≥24000
∴x≤5
∴20-x≥15
答,车间每天至少安排15人才合适。
5.
哪种灯省钱
一种节能灯的功率为10瓦(即0.01千瓦)售价为60元,一种白炽灯功率为60瓦(即0.06千瓦)售价为3元。两种灯的照明效果一样,使用寿命也相同(3000小时以上)如果电费价格为0.5元/千瓦·时,消费者选用哪种灯省钱?
费用=电费+灯的售价
设照明时间为x小时,则节能灯的总费用为
=0.5×0.01x+60
=0.5×0.06x+3
6.为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗如下表:
1
1
年消耗费(万元/台)
200
240
处理污水量(吨/月)
10
12
价格(万元/台)
B型
A型
经预算,该企业购买设备的资金不高于105万元
(1)求购买设备的资金y万元与购买A型x台的函数关系,并设计该企业有几种购买方案
解:
y=12x+10(10-x)
即
y=2x+100
∵y=2x+100≤105
∴
x≤2.5
又∵x是非负整数
∴x可取0、1、2
∴有三种购买方案:①购A型0台,B型10台;②购A型1台,B型9台;③购A型2台,B型8台。
(2)若企业每月产生的污水量为2040吨,利用函数的知识说明,应该选哪种购买方案?
1
1
年消耗费(万元/台)
200
240
处理污水量(吨/月)
10
12
价格(万元/台)
B型
A型
A型x台
则B型10-x台
解:由题意得240x+200(10-x)
≥2040
解得
x≥1
∴x为1或2
∵k>0∴y随x增大而增大。
即:
为节约资金,应选购A型1台,B型9台
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
19.3
课题学习
选择方案
问题一:怎样选取上网收费方式
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选择哪种方式能节省上网费?
下表给出A,B,C三种上宽带网的收费方式.
问题1
怎样选取上网收费方式?
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在
x
>
0
时,考虑何时
(1)
y1
=
y2;
(2)
y1
<
y2;
(3)
y1
>
y2.
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
问题一:怎样选取上网收费方式——分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
你能自己写出方式B的上网费y2关于上网时间
x之间的函数关系式吗?
方式C的上网费y3关于上网时间x之间的函数关系式呢?
你能在同一直角坐标系中画出它们的图象吗?
当x≥0时,y3=120.
问题一:怎样选取上网收费方式——解决问题
当上网时间__________时,
选择方式A最省钱.
当上网时间__________
时,选择方式B最省钱.
当上网时间_________
时,选择方式C最省钱.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
Zx`````x``k
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
问题2
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示
:
问题1:租车的方案有哪几种?
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
共三种:(1)单独租甲种车;
(2)单独租乙种车;
(3)甲种车和乙种车都租.
问题二:怎样租车——分析问题
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
问题二:怎样租车——分析问题
问题4:要使6名教师至少在每辆车上有一名,你能确定
排除哪种方案?你能确定租车的辆数吗?
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
说明了车辆总数不会超过6辆,可以排除方案2——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有
很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分5种情况;
方法2:设租甲种车x辆,确定x的范围.
(1)为使240名师生有车坐,
可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案?为节省费用应选择其中的哪种方案?
问题二:怎样租车——分析问题
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
设租用
x
辆甲种客车,则租车费用y(单位:元)是
x
的函数,即
怎样确定
x
的取值范围呢?
x
辆
(6-x)辆
问题二:怎样租车——解决问题
由函数可知
y
随
x
增大而增大,所以
x
=
4时
y
最小,所以租用4辆甲车,2辆乙车.
变式练习
1000
2000
500
1500
1000
2000
2500
x(km)
y(元)
0
y1
y2
1.某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同.
设汽车每月行驶
x
km,应付给个体车主的月租费是y1元,付给出租公司的月租费是y2
元,y1,y2
分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
当0<x<1500时,租国有的合算.
当x=1500时,租两家的费用一样.
租个体车主的车合算.
变式练习
2.某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折优惠.”若全票价为240元.
(1)设学生数为
x,甲旅行社收费为
y甲,乙旅行社收费为
y乙,分别计算两家旅行社的收费(建立表达式);
zx`````x``k
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
当x
=
4时,两家旅行社的收费一样.
当x
<
4时,甲旅行社优惠;当x
>
4时,乙旅行社优惠.
课堂小结
实际问题
函数模型
实际问题的解
函数模型的解
抽象概括
还原说明
作业布置
?
甲
乙
丙
每辆汽车能装的吨数
2
1
1.5
每吨蔬菜可获利润(元)
500
700
400
1.下表所示为装运甲、乙、丙三种蔬菜的重量及利润.某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只装一种蔬菜).
(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运乙、丙两种蔬菜的汽车各多少辆?
(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售(每种蔬菜不少于一车),如何安排装运,可使公司获得最大利润?最大利润是多少?
某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件。
(1)所获利润y元与制造甲种零件x人关系
(2)若每天所获利润不低于24000元,你认为至少要派多少名工人制造乙种零件合适?
y=6x·150+5(20-x)
·260
y=26000-400x(0≤x≤20)
解:(1)
(2)∵y≥24000
∴26000-400x≥24000
∴x≤5
∴20-x≥15
答,车间每天至少安排15人才合适。
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
最佳方案的选择
哪种灯省钱
一种节能灯的功率为10瓦(即0.01千瓦)售价为60元,一种白炽灯功率为60瓦(即0.06千瓦)售价为3元。两种灯的照明效果一样,使用寿命也相同(3000小时以上)如果电费价格为0.5元/千瓦·时,消费者选用哪种灯省钱?
费用=电费+灯的售价
设照明时间为x小时,则节能灯的总费用为
=0.5×0.01x+60
=0.5×0.06x+3
可利用解析式及图像,结合方程与不等式去说明
y
>y
1
2
y
<y
1
2
即:0.5×0.01x+60=0.5×0.06x+3
x=2280
即:0.5×0.01x+60>0.5×0.06x+3
x<2280
即:0.5×0.01x+60<0.5×0.06x+3
x>2280
答:当x=2280时选用两种灯总费用一样
当x<2280时选用白炽灯总费用省
当x>2280时选用节能灯总费用省
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
作业布置
?
甲
乙
丙
每辆汽车能装的吨数
2
1
1.5
每吨蔬菜可获利润(元)
500
700
400
3.下表所示为装运甲、乙、丙三种蔬菜的重量及利润.某汽车运输公司计划装运甲、乙、丙三种蔬菜到外地销售(每辆汽车按规定满载,并且每辆汽车只装一种蔬菜).
(1)若用8辆汽车装运乙、丙两种蔬菜11吨到A地销售,问装运乙、丙两种蔬菜的汽车各多少辆?
(2)公司计划用20辆汽车装运甲、乙、丙三种蔬菜36吨到B地销售(每种蔬菜不少于一车),如何安排装运,可使公司获得最大利润?最大利润是多少?
4.某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件。
(1)所获利润y元与制造甲种零件x人关系
(2)若每天所获利润不低于24000元,你认为至少要派多少名工人制造乙种零件合适?
y=6x·150+5(20-x)
·260
y=26000-400x(0≤x≤20)
解:(1)
(2)∵y≥24000
∴26000-400x≥24000
∴x≤5
∴20-x≥15
答,车间每天至少安排15人才合适。
5.
哪种灯省钱
一种节能灯的功率为10瓦(即0.01千瓦)售价为60元,一种白炽灯功率为60瓦(即0.06千瓦)售价为3元。两种灯的照明效果一样,使用寿命也相同(3000小时以上)如果电费价格为0.5元/千瓦·时,消费者选用哪种灯省钱?
费用=电费+灯的售价
设照明时间为x小时,则节能灯的总费用为
=0.5×0.01x+60
=0.5×0.06x+3
6.为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗如下表:
1
1
年消耗费(万元/台)
200
240
处理污水量(吨/月)
10
12
价格(万元/台)
B型
A型
经预算,该企业购买设备的资金不高于105万元
(1)求购买设备的资金y万元与购买A型x台的函数关系,并设计该企业有几种购买方案
解:
y=12x+10(10-x)
即
y=2x+100
∵y=2x+100≤105
∴
x≤2.5
又∵x是非负整数
∴x可取0、1、2
∴有三种购买方案:①购A型0台,B型10台;②购A型1台,B型9台;③购A型2台,B型8台。
(2)若企业每月产生的污水量为2040吨,利用函数的知识说明,应该选哪种购买方案?
1
1
年消耗费(万元/台)
200
240
处理污水量(吨/月)
10
12
价格(万元/台)
B型
A型
A型x台
则B型10-x台
解:由题意得240x+200(10-x)
≥2040
解得
x≥1
∴x为1或2
∵k>0∴y随x增大而增大。
即:
为节约资金,应选购A型1台,B型9台
(1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得:
x+y=8
x+1.5y=11,
解得:
x=2
y=6.
答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆;
(2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜的汽车(20-a-b)辆,获得的利润为W百元,由题意得:
2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②,
由①,得
b=a-12.
由②,得
W=4a+b+120
W=4a+a-12+120,
W=5a+108,
∵k=5>0,
∴W随a的增大而增大.
∵
a≥1
b≥1
20-a-b≥1,
∴13≤a≤15.5,
∵a为整数,
∴当a=15时,W最大=5×15+108=183百元,
装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙种蔬菜的汽车2辆
