人教版八年级下册数学 17.1.1探索勾股定理(共36张PPT)
文档属性
| 名称 | 人教版八年级下册数学 17.1.1探索勾股定理(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 923.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览



文档简介
第17章 勾股定理
17.1.1探索勾股定理
1
1
美丽的勾股树
勾股世界
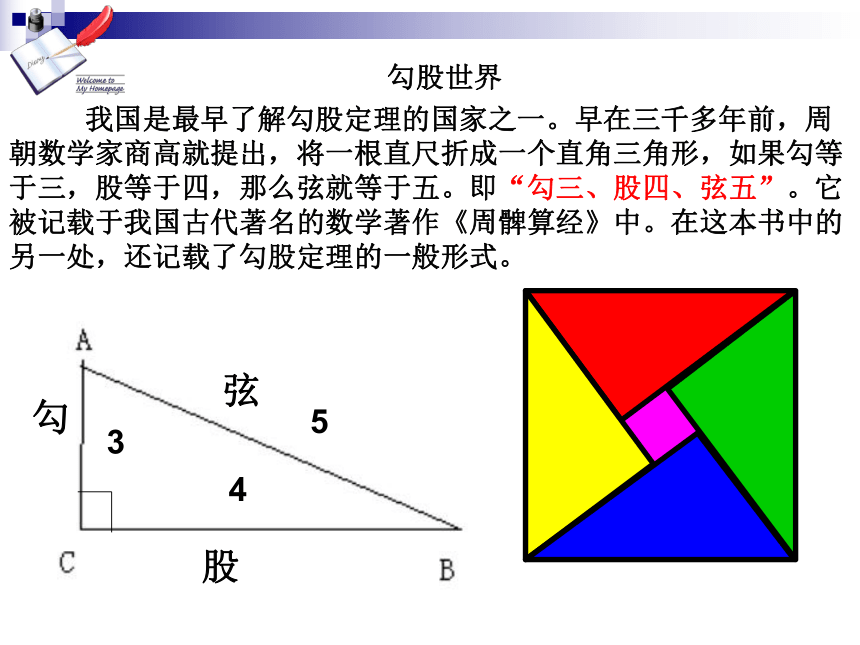
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
弦
5
勾
3
股
4
下图是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
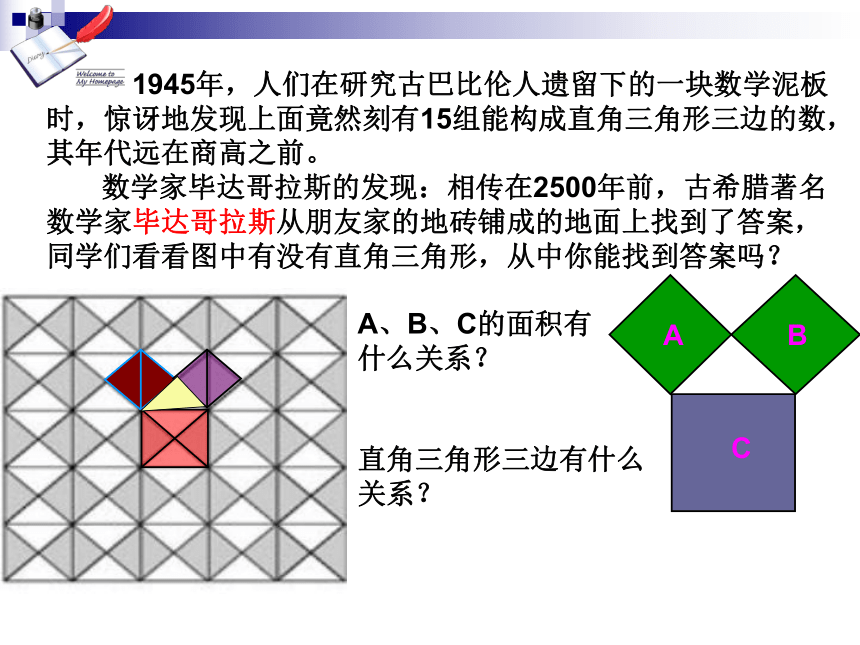
数学家毕达哥拉斯的发现:相传在2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?
A
B
C
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
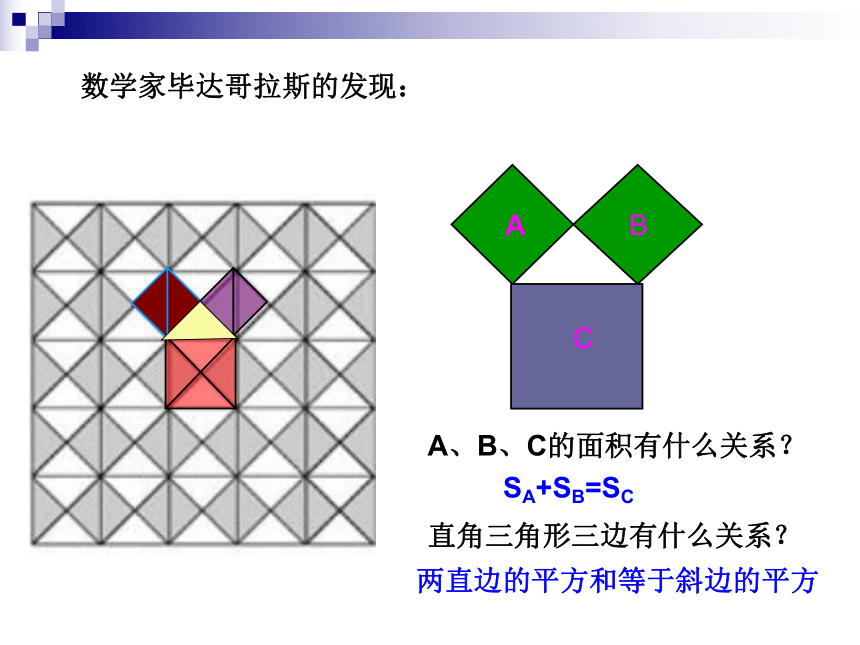
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
探索勾股定理
A
B
C
A
B
C
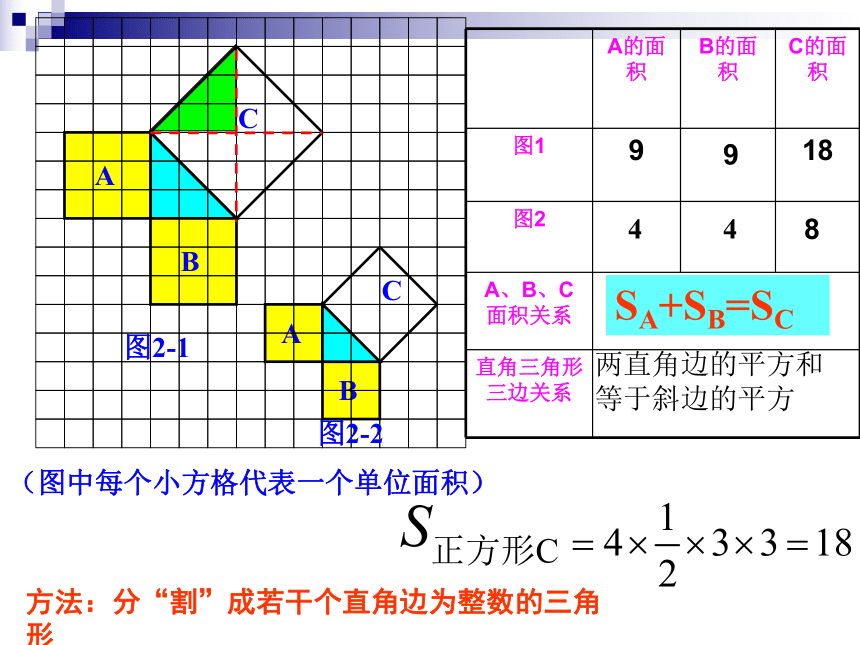
(图中每个小方格代表一个单位面积)
图2-1
图2-2
方法:分“割”成若干个直角边为整数的三角形
SA+SB=SC
4
4
8
两直角边的平方和
等于斜边的平方
9
A的面积
B的面积
C的面积
图1
9
18
图2
A、B、C面积关系
直角三角形三边关系
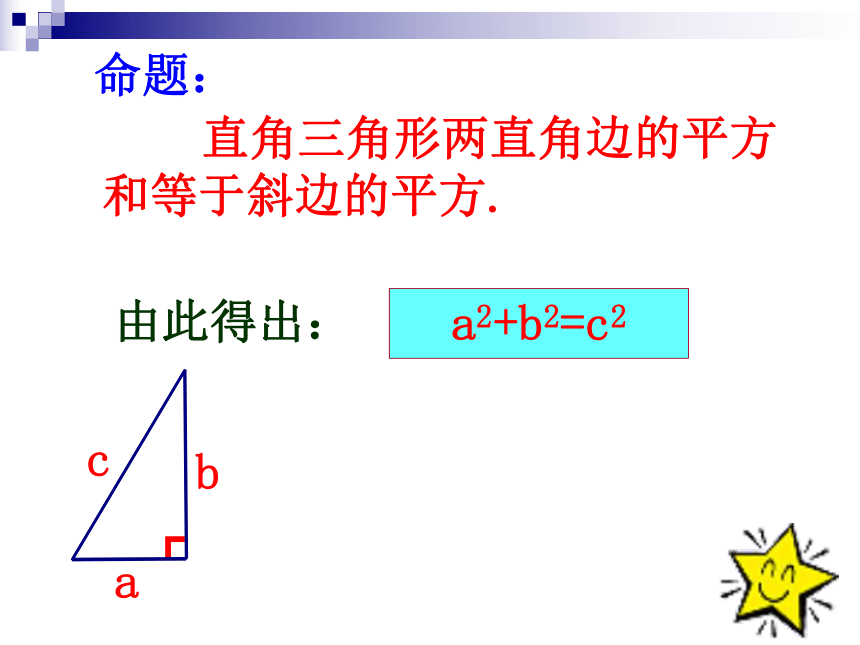
a2+b2=c2
┏
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
命题:
由此得出:
y=0
a
b
c
b
c
b
c
b
c
a
a
a
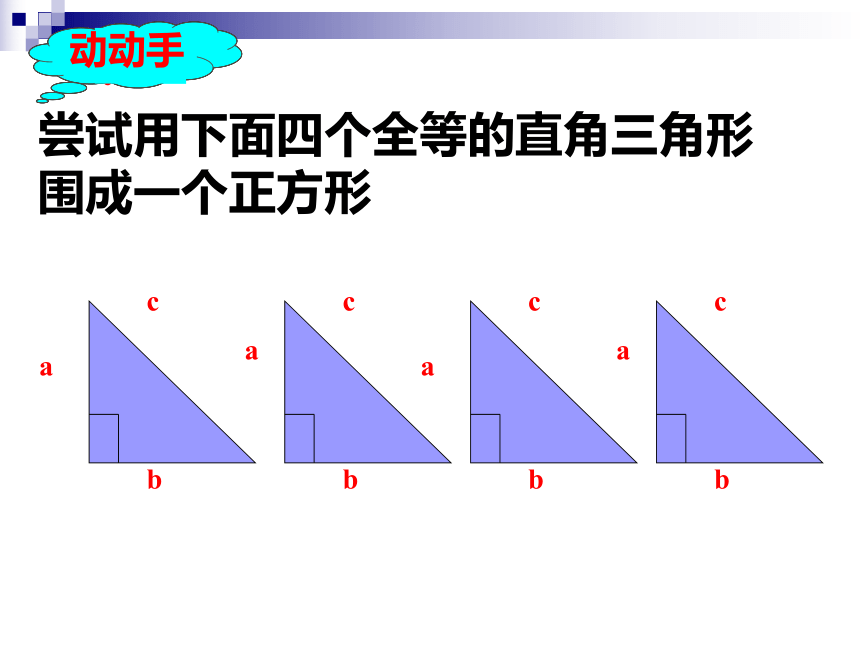
尝试用下面四个全等的直角三角形
围成一个正方形
动动手
a
c
b
a
b
c
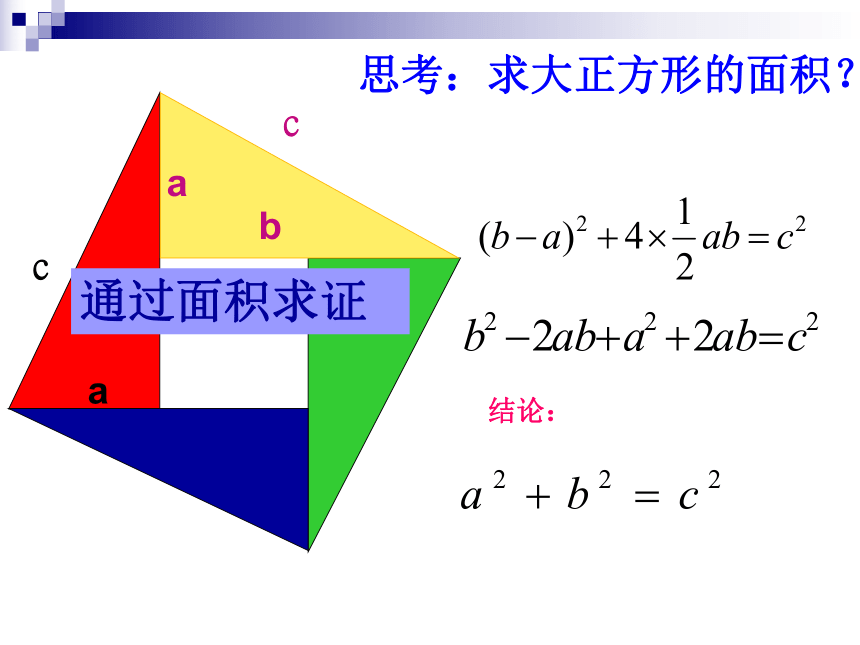
思考:求大正方形的面积?
结论:
通过面积求证
a
b
c
a
b
c
b
a
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
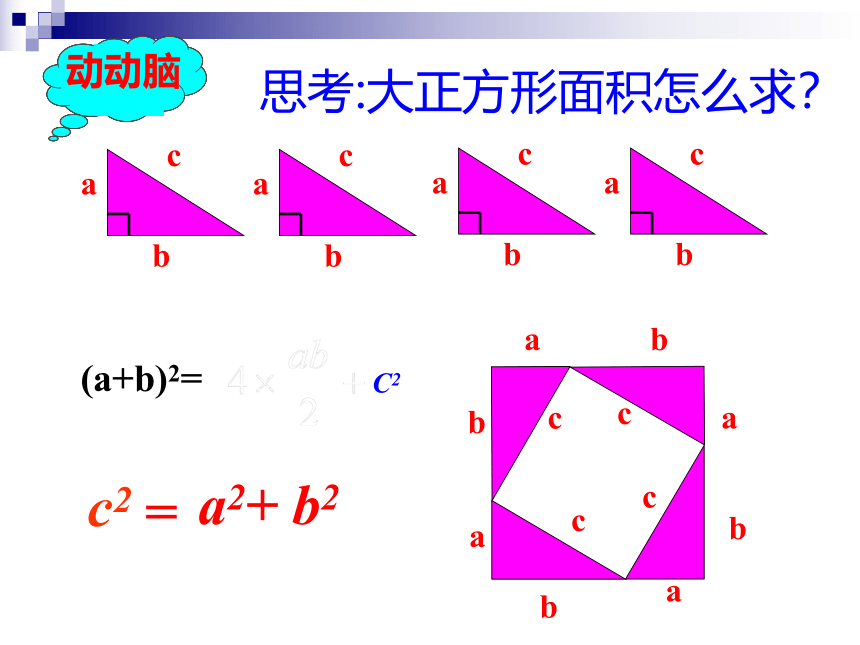
(a+b)2=
C2
a2+ b2
c2
=
y=0
动动脑
思考:大正方形面积怎么求?
勾股定理:
如果直角三角形两直角边分别 为a、b,斜边为c,那么
即 直角三角形两直角边 的平方和等于斜边的平方。
a
b
c
勾
股
弦
y=0
证明结论得到定理
经过证明被确认正确的命题叫做定理.
y=0
例.求出下列直角三角形中未知边的长度
6
8
x
5
x
13
学以致用,做一做
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
x2+52=132
x2=132-52
x2=144
∴ x=12
(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2
∵x>0
A
C
B
A
C
B
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
x =81+144
2
y =169-144
z =625-576
2
2
x =15
y=5
z=7
尝试用勾股定理解答问题
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法:
8
x
17
16
20
x
12
5
x
3.在Rt△ABC中, ∠C=90°
(1)已知 a=5 ,b=12 . 那么 c =_____.
(2)已知 b=9 ,c=15 . 那么 a =_____.
(3)已知 ∠A=30°, c=8 ,
则a=_____,b=_____.
13
4
12
C
160
90
40
40
B
A
4.如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.
(单位:毫米)
本节课从知识、能力方面你有哪些收获?
直角三角形两直角边的平方和等于斜边的平方.
勾股定理:
1.一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板
能否从门框内通过?为什么?
D C
A B
2m
1m
用勾股定理解决实际问题
结论:
S1+S2+S3+S4
=S5+S6
=S7
2.
1
1
美丽的勾股树
3.小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒多少根?
4.小亮想知道学校旗杆的高度.他发现旗杆上的绳子垂到地面还多2米;当他把绳子的下端拉开4米后,下端刚好接触地面.你能帮他把学校旗杆的高求出来吗?
5.如图是一个机器零件示意图,∠ACD=90°是这种零件合格的一项指标.现测得AB=4cm,BC=3cm,CD=12cm,AD=13cm,∠ABC=90°.根据这些条件,能否知道∠ACD等于90°?
A
C
B
D
6.一个中学生探险队走地下迷宫(如图),他们从入口A出发,利用随身携带的仪器,测得先向东走了10km,然后又向北行走了6km,接着又向西走了3km,再向北走9km,最后向东一拐,仅走1km就找到了出口B.你能帮他们计算出出口点B与入口点A的直线距离有多远吗?
A
10
6
3
9
1
B
7.一长方形水池的长、宽、高分别为12dm、4dm、3dm,池中有一满池水.小亮把长度为14dm的金属棒放入水中,能否被完全淹没?
说说你的理由.
8.如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.请问:蚂蚁爬到食物处的最近路线是多长?
A
B
9.我们知道数轴上的点有的表示有理数,有的表示无理数,那么 这个数你能用数轴上的点来表示吗?
l
作法:
1.在数轴上找点A,使OA=1;
0
1
A
2.作直线l垂直于OA,在l上取点B,使AB=1;
B
C
3.以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
归纳结论:
只要能画出长为 的线段,就能在数轴上画出表示这个数的点.
是两条直角边都是1的直角三角形的斜边.
思考与探究
怎样作出为 , , , ,
……的线段呢?请你画出来,并说说理由.
利用勾股定理,构造直角三角形,我们就可以得到长为 , , ……的线段,如下图.
从而在数轴上画出表示 , , ……的点.
1
1
1
1
1
1
1
1
1
1
1
1
1
Sa+Sb=Sc
5.以直角三角形三边为半径作半圆,这3个半圆的面积之间有什么关系?
10.长为 的线段是直角边为正整数______,______的直角三角形的斜边.
长为 的线段是直角边为正整数______,______的直角三角形的斜边.
2
1
2
3
11.如图,等边三角形的边长是6:
(1)求高AD的长(精确到0.001);
(2)求这个三角形的面积(精确到0.01).
A
B
C
D
17.1.1探索勾股定理
1
1
美丽的勾股树
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
弦
5
勾
3
股
4
下图是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
数学家毕达哥拉斯的发现:相传在2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?
A
B
C
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
探索勾股定理
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
方法:分“割”成若干个直角边为整数的三角形
SA+SB=SC
4
4
8
两直角边的平方和
等于斜边的平方
9
A的面积
B的面积
C的面积
图1
9
18
图2
A、B、C面积关系
直角三角形三边关系
a2+b2=c2
┏
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
命题:
由此得出:
y=0
a
b
c
b
c
b
c
b
c
a
a
a
尝试用下面四个全等的直角三角形
围成一个正方形
动动手
a
c
b
a
b
c
思考:求大正方形的面积?
结论:
通过面积求证
a
b
c
a
b
c
b
a
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
(a+b)2=
C2
a2+ b2
c2
=
y=0
动动脑
思考:大正方形面积怎么求?
勾股定理:
如果直角三角形两直角边分别 为a、b,斜边为c,那么
即 直角三角形两直角边 的平方和等于斜边的平方。
a
b
c
勾
股
弦
y=0
证明结论得到定理
经过证明被确认正确的命题叫做定理.
y=0
例.求出下列直角三角形中未知边的长度
6
8
x
5
x
13
学以致用,做一做
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
x2+52=132
x2=132-52
x2=144
∴ x=12
(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2
∵x>0
A
C
B
A
C
B
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
x =81+144
2
y =169-144
z =625-576
2
2
x =15
y=5
z=7
尝试用勾股定理解答问题
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法:
8
x
17
16
20
x
12
5
x
3.在Rt△ABC中, ∠C=90°
(1)已知 a=5 ,b=12 . 那么 c =_____.
(2)已知 b=9 ,c=15 . 那么 a =_____.
(3)已知 ∠A=30°, c=8 ,
则a=_____,b=_____.
13
4
12
C
160
90
40
40
B
A
4.如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.
(单位:毫米)
本节课从知识、能力方面你有哪些收获?
直角三角形两直角边的平方和等于斜边的平方.
勾股定理:
1.一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板
能否从门框内通过?为什么?
D C
A B
2m
1m
用勾股定理解决实际问题
结论:
S1+S2+S3+S4
=S5+S6
=S7
2.
1
1
美丽的勾股树
3.小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒多少根?
4.小亮想知道学校旗杆的高度.他发现旗杆上的绳子垂到地面还多2米;当他把绳子的下端拉开4米后,下端刚好接触地面.你能帮他把学校旗杆的高求出来吗?
5.如图是一个机器零件示意图,∠ACD=90°是这种零件合格的一项指标.现测得AB=4cm,BC=3cm,CD=12cm,AD=13cm,∠ABC=90°.根据这些条件,能否知道∠ACD等于90°?
A
C
B
D
6.一个中学生探险队走地下迷宫(如图),他们从入口A出发,利用随身携带的仪器,测得先向东走了10km,然后又向北行走了6km,接着又向西走了3km,再向北走9km,最后向东一拐,仅走1km就找到了出口B.你能帮他们计算出出口点B与入口点A的直线距离有多远吗?
A
10
6
3
9
1
B
7.一长方形水池的长、宽、高分别为12dm、4dm、3dm,池中有一满池水.小亮把长度为14dm的金属棒放入水中,能否被完全淹没?
说说你的理由.
8.如图所示,圆柱形玻璃容器的高为18cm,底面周长为24cm,在外侧距下底1cm的点A处有一小蚂蚁,它在与自己相对的圆柱形容器的上口外侧距开口1cm的点B处发现一点点食物碎屑.请问:蚂蚁爬到食物处的最近路线是多长?
A
B
9.我们知道数轴上的点有的表示有理数,有的表示无理数,那么 这个数你能用数轴上的点来表示吗?
l
作法:
1.在数轴上找点A,使OA=1;
0
1
A
2.作直线l垂直于OA,在l上取点B,使AB=1;
B
C
3.以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
归纳结论:
只要能画出长为 的线段,就能在数轴上画出表示这个数的点.
是两条直角边都是1的直角三角形的斜边.
思考与探究
怎样作出为 , , , ,
……的线段呢?请你画出来,并说说理由.
利用勾股定理,构造直角三角形,我们就可以得到长为 , , ……的线段,如下图.
从而在数轴上画出表示 , , ……的点.
1
1
1
1
1
1
1
1
1
1
1
1
1
Sa+Sb=Sc
5.以直角三角形三边为半径作半圆,这3个半圆的面积之间有什么关系?
10.长为 的线段是直角边为正整数______,______的直角三角形的斜边.
长为 的线段是直角边为正整数______,______的直角三角形的斜边.
2
1
2
3
11.如图,等边三角形的边长是6:
(1)求高AD的长(精确到0.001);
(2)求这个三角形的面积(精确到0.01).
A
B
C
D
