人教版八年级下册数学课件:19.1.1变量与函数 习题课(共16张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:19.1.1变量与函数 习题课(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 815.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 18:39:22 | ||
图片预览






文档简介
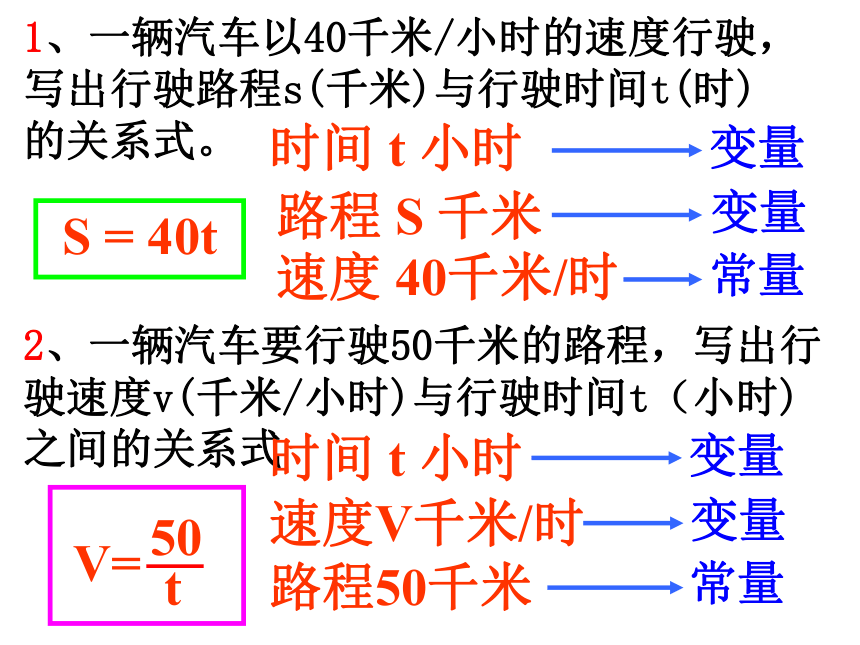
1、一辆汽车以40千米/小时的速度行驶,
写出行驶路程s(千米)与行驶时间t(时)
的关系式。
2、一辆汽车要行驶50千米的路程,写出行驶速度v(千米/小时)与行驶时间t(小时)之间的关系式
S = 40t
时间 t 小时
速度 40千米/时
路程 S 千米
V=
t
50
变量
变量
常量
时间 t 小时
路程50千米
速度V千米/时
变量
变量
常量
V
R
Q=40-5t
其中变量是 、 ,常量是 .
3.若球体体积为V,半径为R,则V=
3
3
4.汽车开始行使时油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q升与行使时间t小时的关系是是 . 并指出其中的常量是 ,变量是
Q、t
40、5
5. 小明到商店买练习簿,每本单价2元,购买的总数 x(本)与总金额 y(元)的关系式,可以表示为:
y = 2x
6. 每张电影票售价为10元,如果早场售出票150张,日场售出票205张,晚场售出310张. 三场电影的票房收入各多少元?设一场电影售票x张,票房收入y元。怎样用含x的式子表示 y ?
(2) 关系式为:y=10x
(1) 早场电影票收入:150×10=1500元
日场电影票收入:205×10=2050元
晚场电影票收入:310×10=3100元
7.在一根弹簧的下端悬挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律。如果弹簧原长10cm,每1kg的重物使弹簧伸长0.5cm,怎样用含有重物质量m的的式子表示受力后弹簧的长度l?
挂1kg重物时弹簧的长度:1×0.5+10=10.5(cm)
关系式为: l =0.5m+10
探究:
结论:
挂2kg重物时弹簧的长度:2×0.5+10=11(cm)
挂3kg重物时弹簧的长度:3×0.5+10=11.5(cm)
8. 要画一个面积为10 圆,圆的半径应取多少?圆的面积为20 呢?怎样用含有圆面积S的式子表示圆半径r?
探究:
圆面积公式
面积为10 的圆半径 ≈ 1.78(cm)
面积为20 的圆半径 ≈ 2.52(cm)
关系式为:
9.用10cm长的绳子围成矩形,试改变矩形的长、宽,观察矩形的面积怎样变化,试举出三组长、宽的值。计算相应矩形的面积的值,然后探索它们的变化规律:设矩形的长度为xm,面积为Sm2 ,怎样用含x的式子表示S?
1
用10cm长的绳子围成矩形,试改变矩形的长、宽,观察矩形的面积怎样变化,试举出三组长、宽的值。计算相应矩形的面积的值,然后探索它们的变化规律:设矩形的长度为xm,面积为S ,怎样用含x的式子表示S?
S= x (5-x)
.
长 x 米
宽 (5-x) 米
4
3
2.5
1
2
2.5
面积 s 米2
4
6
6.25
解:
10.一个三角形的底边长5cm,高h可以任意伸缩.写出面积S随h变化关系式,并指出其中的常量与变量.
S = h
5
2
解:
变量是 s 、h
常量是
5
2
11.夏季高山上温度从山脚起每升高100米降低 0.7℃,已知山脚下温度是23℃,写出温度y ℃与上升高度 Xm之间的关系式,并指出其中的常量与变量。
解:
y =23 -0.007x
变量是 x 、y
常量是 23、0.007
12、指出下面各个问题中,哪些量是
变量,哪些量是常量?
(1)如果直角三角形中一锐角的度数为 ,另一个锐角的度数为 ,试用含 的式子表示 .
解:
常量是 90
变量是 、
= 900 -
解:
变量是 、
常量是
(2)如果某种报纸的单价为 元, 表示购买这种报纸的份数, (元)表示买报纸的总价,试用含 的式子表示 .
13 瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式.
瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式.
1
2
3
…
x
y
…
1
1+2
1+2+3
1+2+3+ …+x
瓶子总数y 与层数x之间的关系式:
x
写出行驶路程s(千米)与行驶时间t(时)
的关系式。
2、一辆汽车要行驶50千米的路程,写出行驶速度v(千米/小时)与行驶时间t(小时)之间的关系式
S = 40t
时间 t 小时
速度 40千米/时
路程 S 千米
V=
t
50
变量
变量
常量
时间 t 小时
路程50千米
速度V千米/时
变量
变量
常量
V
R
Q=40-5t
其中变量是 、 ,常量是 .
3.若球体体积为V,半径为R,则V=
3
3
4.汽车开始行使时油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q升与行使时间t小时的关系是是 . 并指出其中的常量是 ,变量是
Q、t
40、5
5. 小明到商店买练习簿,每本单价2元,购买的总数 x(本)与总金额 y(元)的关系式,可以表示为:
y = 2x
6. 每张电影票售价为10元,如果早场售出票150张,日场售出票205张,晚场售出310张. 三场电影的票房收入各多少元?设一场电影售票x张,票房收入y元。怎样用含x的式子表示 y ?
(2) 关系式为:y=10x
(1) 早场电影票收入:150×10=1500元
日场电影票收入:205×10=2050元
晚场电影票收入:310×10=3100元
7.在一根弹簧的下端悬挂重物,改变并记录重物的质量,观察并记录弹簧长度的变化,探索它们的变化规律。如果弹簧原长10cm,每1kg的重物使弹簧伸长0.5cm,怎样用含有重物质量m的的式子表示受力后弹簧的长度l?
挂1kg重物时弹簧的长度:1×0.5+10=10.5(cm)
关系式为: l =0.5m+10
探究:
结论:
挂2kg重物时弹簧的长度:2×0.5+10=11(cm)
挂3kg重物时弹簧的长度:3×0.5+10=11.5(cm)
8. 要画一个面积为10 圆,圆的半径应取多少?圆的面积为20 呢?怎样用含有圆面积S的式子表示圆半径r?
探究:
圆面积公式
面积为10 的圆半径 ≈ 1.78(cm)
面积为20 的圆半径 ≈ 2.52(cm)
关系式为:
9.用10cm长的绳子围成矩形,试改变矩形的长、宽,观察矩形的面积怎样变化,试举出三组长、宽的值。计算相应矩形的面积的值,然后探索它们的变化规律:设矩形的长度为xm,面积为Sm2 ,怎样用含x的式子表示S?
1
用10cm长的绳子围成矩形,试改变矩形的长、宽,观察矩形的面积怎样变化,试举出三组长、宽的值。计算相应矩形的面积的值,然后探索它们的变化规律:设矩形的长度为xm,面积为S ,怎样用含x的式子表示S?
S= x (5-x)
.
长 x 米
宽 (5-x) 米
4
3
2.5
1
2
2.5
面积 s 米2
4
6
6.25
解:
10.一个三角形的底边长5cm,高h可以任意伸缩.写出面积S随h变化关系式,并指出其中的常量与变量.
S = h
5
2
解:
变量是 s 、h
常量是
5
2
11.夏季高山上温度从山脚起每升高100米降低 0.7℃,已知山脚下温度是23℃,写出温度y ℃与上升高度 Xm之间的关系式,并指出其中的常量与变量。
解:
y =23 -0.007x
变量是 x 、y
常量是 23、0.007
12、指出下面各个问题中,哪些量是
变量,哪些量是常量?
(1)如果直角三角形中一锐角的度数为 ,另一个锐角的度数为 ,试用含 的式子表示 .
解:
常量是 90
变量是 、
= 900 -
解:
变量是 、
常量是
(2)如果某种报纸的单价为 元, 表示购买这种报纸的份数, (元)表示买报纸的总价,试用含 的式子表示 .
13 瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式.
瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式.
1
2
3
…
x
y
…
1
1+2
1+2+3
1+2+3+ …+x
瓶子总数y 与层数x之间的关系式:
x
