人教版八年级下册数学课件:19.1变量与函数(共15张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:19.1变量与函数(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 18:38:15 | ||
图片预览





文档简介
上
课
啦 !
变量与函数
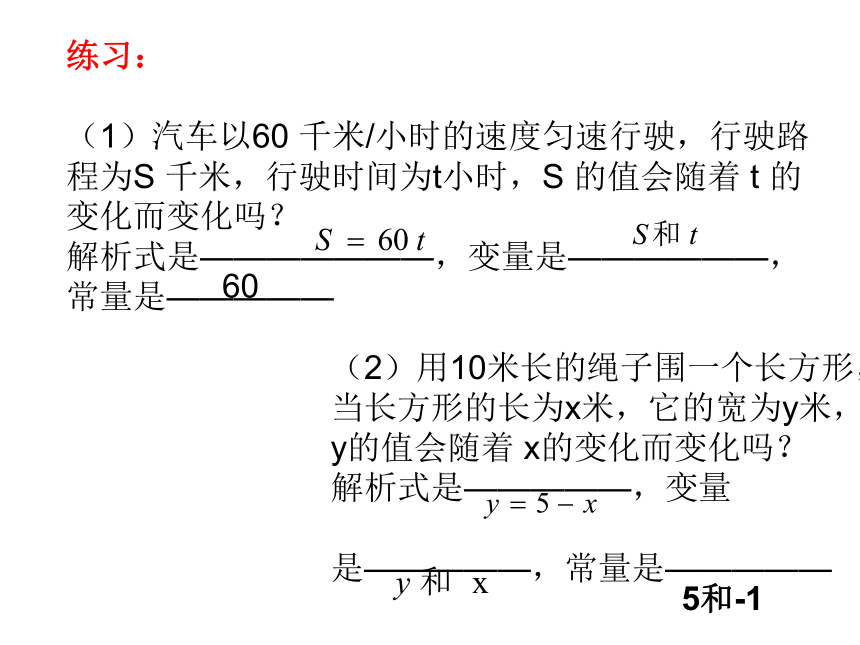
练习:
(1)汽车以60 千米/小时的速度匀速行驶,行驶路程为S 千米,行驶时间为t小时,S 的值会随着 t 的变化而变化吗?
解析式是———————,变量是——————,常量是—————
(2)用10米长的绳子围一个长方形,当长方形的长为x米,它的宽为y米,y的值会随着 x的变化而变化吗?
解析式是—————,变量
是—————,常量是—————
60
5和-1
在一个变化过程中:
1、数值发生变化的量——变量(2个)
2、数值始终不变的量——常量(数字,包括“+、-”)
注意:
等式右边的式子是:(1)单项式:变量有2个,常量有1个;(2)多项式:变量有2个,常量有2个及2个以上(数字和“+、-”符号)
3、如果有2个变量x和y(x先变化,y后变化),并且对于x的每一个确定的数值,都有唯一的一个y数值与之相对应(一个x只能有一个y值,简称“一一对应”关系)
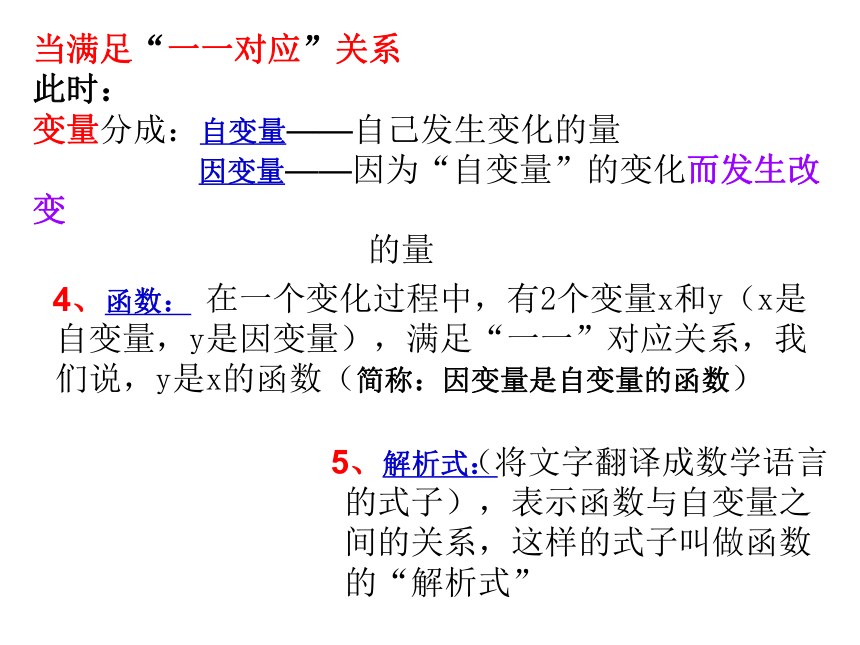
当满足“一一对应”关系
此时:
变量分成:自变量——自己发生变化的量
因变量——因为“自变量”的变化而发生改变
的量
在一个变化过程中,有2个变量x和y(x是自变量,y是因变量),满足“一一”对应关系,我们说,y是x的函数(简称:因变量是自变量的函数)
(将文字翻译成数学语言的式子),表示函数与自变量之间的关系,这样的式子叫做函数的“解析式”
4、函数:
5、解析式:
例:下列关于变量x、y的关系:
(1) (2)
(3) (4)
其中,y是x的函数的是——————
(1)、(4)
1、有些式子要进行移项,做适当的变形,通常是“y=……”的样子,等号左边只有一个字母
2、判断方法(代特殊值):当x=1时,y=?;当x=2时,y=?以此验证是否“一一对应”
注意:
是函数的条件:
解析式中:
(1)有2个变量;
(2)满足“一一对应”关系(一个x只能有一个y值)
例:已知三角形底边长为4,高为x,三角形的面积为 S,则S与x的函数解析式_______________
当x=3时,y=_____,
当x= 时,y=_____
y=2x
6
7
若当x=A时,y=B,
称:“B”是函数解析式中,自变
量=“A” 时的函数值
例:解析式y=x-1,求当x= 时,y=?
解:
6、函数值:
7、自变量的取值范围: 使得式子有意义的x的取值
例:求下列函数中自变量x的取值范围:
( 请看黑板例题)
求取值范围的方法:
(1)式子是整式,自变量的取值范围是:全体实数(正数、0、负数)
(2)式子是分式,自变量的取值范围是:分母 0
(3)式子是二次根式,自变量的取值范围是:被开方数 0
(4)式子中既有分式,也有二次根式等式子时,自变量的取值范围是:列不等式组,使得所有的式子同时有意义,(求不等式组的解集)
(5)式子是0次幂,自变量的取值范围是:底数 0
1.分别指出下列各式中的常量与变量.
(1)圆的面积公式s=πr2.
(2)正方形的周长公式l=4a.
(3)汽车的速度为50km/h,则行驶的时间t(h)与行驶路程s之间的关系是s=50t.
随堂练习
2.分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积S(cm2)与这边上的高h(cm)的关系式是 ;
(2)若直角三角形中的一个锐角的度数为α,则另一个锐角β(度)与α间的关系式是β=90-α ;
(3)若某种报纸的单价为a元,x表示购买这种报纸的份数,则购买报纸的总价y(元)与x间的关系是y=ax.
你学到了什么?
1、变量
2、常量
3、自变量,因变量
4、函数
5、解析式
6、函数值
7、求函数中自变量的取值范围
下
课
啦 !
课
啦 !
变量与函数
练习:
(1)汽车以60 千米/小时的速度匀速行驶,行驶路程为S 千米,行驶时间为t小时,S 的值会随着 t 的变化而变化吗?
解析式是———————,变量是——————,常量是—————
(2)用10米长的绳子围一个长方形,当长方形的长为x米,它的宽为y米,y的值会随着 x的变化而变化吗?
解析式是—————,变量
是—————,常量是—————
60
5和-1
在一个变化过程中:
1、数值发生变化的量——变量(2个)
2、数值始终不变的量——常量(数字,包括“+、-”)
注意:
等式右边的式子是:(1)单项式:变量有2个,常量有1个;(2)多项式:变量有2个,常量有2个及2个以上(数字和“+、-”符号)
3、如果有2个变量x和y(x先变化,y后变化),并且对于x的每一个确定的数值,都有唯一的一个y数值与之相对应(一个x只能有一个y值,简称“一一对应”关系)
当满足“一一对应”关系
此时:
变量分成:自变量——自己发生变化的量
因变量——因为“自变量”的变化而发生改变
的量
在一个变化过程中,有2个变量x和y(x是自变量,y是因变量),满足“一一”对应关系,我们说,y是x的函数(简称:因变量是自变量的函数)
(将文字翻译成数学语言的式子),表示函数与自变量之间的关系,这样的式子叫做函数的“解析式”
4、函数:
5、解析式:
例:下列关于变量x、y的关系:
(1) (2)
(3) (4)
其中,y是x的函数的是——————
(1)、(4)
1、有些式子要进行移项,做适当的变形,通常是“y=……”的样子,等号左边只有一个字母
2、判断方法(代特殊值):当x=1时,y=?;当x=2时,y=?以此验证是否“一一对应”
注意:
是函数的条件:
解析式中:
(1)有2个变量;
(2)满足“一一对应”关系(一个x只能有一个y值)
例:已知三角形底边长为4,高为x,三角形的面积为 S,则S与x的函数解析式_______________
当x=3时,y=_____,
当x= 时,y=_____
y=2x
6
7
若当x=A时,y=B,
称:“B”是函数解析式中,自变
量=“A” 时的函数值
例:解析式y=x-1,求当x= 时,y=?
解:
6、函数值:
7、自变量的取值范围: 使得式子有意义的x的取值
例:求下列函数中自变量x的取值范围:
( 请看黑板例题)
求取值范围的方法:
(1)式子是整式,自变量的取值范围是:全体实数(正数、0、负数)
(2)式子是分式,自变量的取值范围是:分母 0
(3)式子是二次根式,自变量的取值范围是:被开方数 0
(4)式子中既有分式,也有二次根式等式子时,自变量的取值范围是:列不等式组,使得所有的式子同时有意义,(求不等式组的解集)
(5)式子是0次幂,自变量的取值范围是:底数 0
1.分别指出下列各式中的常量与变量.
(1)圆的面积公式s=πr2.
(2)正方形的周长公式l=4a.
(3)汽车的速度为50km/h,则行驶的时间t(h)与行驶路程s之间的关系是s=50t.
随堂练习
2.分别指出下列各关系式中的变量与常量:
(1)三角形的一边长5cm,它的面积S(cm2)与这边上的高h(cm)的关系式是 ;
(2)若直角三角形中的一个锐角的度数为α,则另一个锐角β(度)与α间的关系式是β=90-α ;
(3)若某种报纸的单价为a元,x表示购买这种报纸的份数,则购买报纸的总价y(元)与x间的关系是y=ax.
你学到了什么?
1、变量
2、常量
3、自变量,因变量
4、函数
5、解析式
6、函数值
7、求函数中自变量的取值范围
下
课
啦 !
