人教版初中数学七年级下册9.2.2《一元一次不等式的应用》课件(共22张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册9.2.2《一元一次不等式的应用》课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览






文档简介
§.9 不等式与不等式组
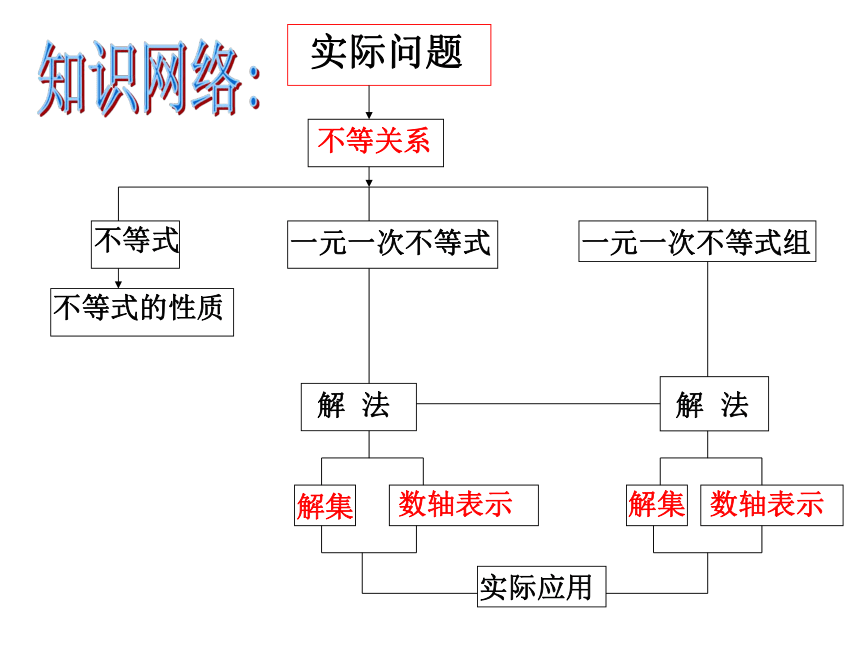
实际问题
不等关系
不等式
一元一次不等式
一元一次不等式组
不等式的性质
解集
解集
数轴表示
数轴表示
解 法
解 法
实际应用
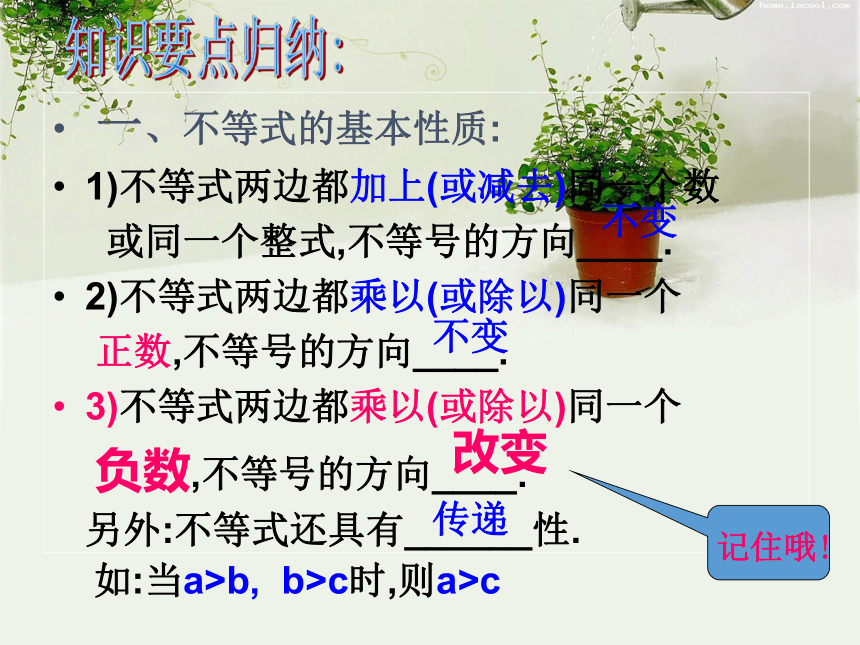
一、不等式的基本性质:
1)不等式两边都加上(或减去)同一个数
或同一个整式,不等号的方向____.
2)不等式两边都乘以(或除以)同一个
正数,不等号的方向____.
3)不等式两边都乘以(或除以)同一个
负数,不等号的方向____.
另外:不等式还具有______性.
如:当a>b, b>c时,则a>c
不变
不变
改变
记住哦!
传递
解一元一次不等式和解一元一次方程类似,有
①去分母 ②去括号 ③移项 ④ 合并同类项
⑤系数化为1等步骤.
它们的区别在哪里呢?
在系数化为1的这一步中,要特别注意
不等式的两边都乘以(或除以)一
个负数时,不等号的方向必须改变方向.
1、一元一次不等式的解法
二、方法与过程
2、一元一次不等式组的解法
(1)、先分别求出不等式组中各个不等式的解集。
(2)、利用数轴找出各个不等式的 解集的公共部分。
(3)、写出不等式组的解集。
特别注意:用数轴表示不等式的解集时,” <、>“用空心,” ≤、≥“用实心。” >、≥“向右画,” <、≤“向左画。
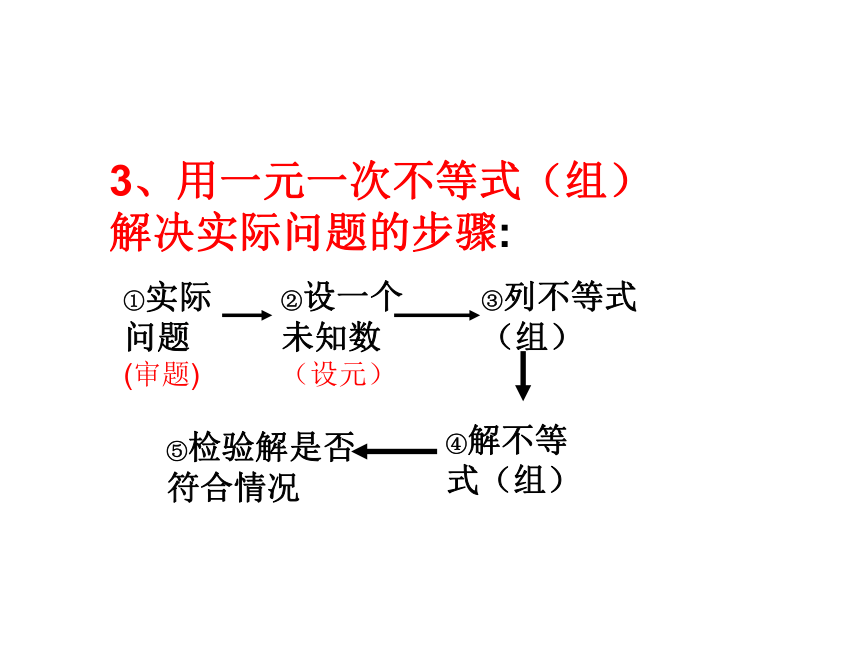
3、用一元一次不等式(组)解决实际问题的步骤:
①实际 问题(审题)
②设一个未知数(设元)
③列不等式(组)
④解不等式(组)
⑤检验解是否符合情况
三、题型大揭秘
(一)、用定义解题
⒈下列不等式中,是一元一次不等式的( )。
2.若
是关于x的一元一次不等式,则
该不等式的解集为:
D
(二)、数轴题
1、a,b两个实数在数轴上的对应点如图所示,用“<”或“>”号填空:
a__b; |a|____|b|; a+b___0 a-b__0; a+b___a-b;
2.一个不等式的解集如图所示,则这个不等式的正整数解是________.
(三)利用不等式性质进行同等变换
1、与2x<6不同解的不等式是( )
A.2x+1<7 B.4x<12
C.-4x>-12 D.-2x<-6
2、如果m<n<0,那么下列结论中错误的是( )
A、m-9<n-9 B、-m>-n
D、
C、
(四)限制条件的解
1.不等式3(x-2)≤x+4的非
负整数解有几个.( )
A.4 B.5 C.6 D.无数个
2.如果3+2x是正数,
则x的取值范围是_____,
如果3+2x是非负数,则
x的取值范围是________.
(五)已知解集求范围
1.若(a-1)x A、a>0 B、a<0
C、a<1 D、a>1
2.关于x的方程5-a(1-x)=8x-(3-a)x的解是负数,则a的取值范围是( )
A、a<-4 B、a>5
C、a>-5 D、a<-5
3、如果不等式4x-3a>-1与不等式
2(x-1)+3>5的解集相同,请确定a的值.
(六)求不等式的特殊解
1.求x+3<6的所有正整数解。
解:x<3
∴ x+3<6的正整数解为1、2
2.求10-4(x-3)≥2(x-1)的非负整数解,并在数轴上表示出来。
3、若不等式2x-a>x的唯一负整数解释-1,
则a的取值范围是?
(七)确定方程或不等式中的字母及
应用中取值范围
1、在平面直角坐标系中若点P(m-3,m+1)在第二象限,则m的取值范围为( )
A.-1<m<3 B.m>3
C.m<-1 D.m>-1
2、已知关于x的方程
的解是非负整数,求m的取值范围?
(八)由解集求最值
1、若3x+4≤6+2(x-2),则x+1的
绝对值的最小值是多少?
2、已知关于x的不等式组
{
X-a≥0
5-2x>1
,只有5个整数解,则a的
取值范围是多少?
(九)实际问题与不等式(组)
Ⅰ、借不等式解不定方程。(方案问题)
七年级某班为了奖励学习进步的学生,购买了
单价为3元的笔记本和单价为5元的钢笔两种
奖品共花费了35元,则有几种购买方案?
解:设购买了单价为3元的笔记本m本,
购买了单价为5元的钢笔n支。则由题意列
方程:
3m+5n=35
∴
m=7-0.6m
因为m 和n是正整数
所以n=7- 0.6m为正整数,
则 0.6m为小于7的正整数,
可知m为5的倍数
∴{
m>0
.
∴
7- 0.6m>0
所以 m=5或者10
则n=4或者1
答:有2种购买方案①购买笔记本5本,钢笔4支
②购买笔记本10本,购买钢笔1支。
0Ⅱ、用不等式组确定最优方案问题
某单位给某小学捐献一批饮用水和蔬菜共320件
,其中饮用水比蔬菜多80件。
(1)求捐献了饮用水和蔬菜个多少件?
(2)现在计划用甲乙两种汽车共八辆一次性运输
这批饮用水和蔬菜到某小学。已知每辆甲种车最
多可装40件应用水和10件蔬菜,每辆已种汽车最
多能装饮用水和蔬菜各20件。已知每辆甲种货车
付运费400元,乙种货车副运费360元则可以有几
种方案来安排甲乙两种货车运输?哪种方案花费
最少?
解 (1)设饮用水x件,蔬菜y件。
根据题意列方程组,得
{
x+y=320
x-y=80
解,得
{
x=200
y=120
答:饮用水和蔬菜分别为200件和120件。
(2)设租用甲种车m辆,则租用乙种车(8-m)辆
依据题意,得
{
40m+20(8-m) ≥200
10m+20(8-m) ≥120
解,得2≤m≤4
因为m为正整数,所以m=2、3、4
所以安排甲乙两种车的时候有三种方案:
①甲种车2辆,乙种车6辆;
②甲种车3辆,乙种车5辆;
③甲种车4辆,乙种车4辆。
三种方案的运输费为:
①2×400+6×360=2960(元)
②3×400+5×360=3000(元)
③4×400+4×360=3040 (元)
所以使用第一种方案所用的方案运费最少为2960元。
所以应选择2辆甲种车,6辆乙种车。
总结:
从此例题种可看出,列不等式组解决方案问题
的思路一般是:
1、列出不等式组求出解集;
2、根据问题的实际意义确定出不等式组的一些
特殊解;
3、找出相应的可行性方案;
4、通过计算、比较,确定出最优方案。
{
课后练习:
1、将一批货物装箱,若每箱装8小包,则最后
一箱还差3包;若每箱装5包,则剩余的货物大于9包
且小于17包。这些货物共有多少个小包?多少个箱子?
2、若不等式组
{
3x-4≤0
X-a≥0
无解,则a的取值范围是?
实际问题
不等关系
不等式
一元一次不等式
一元一次不等式组
不等式的性质
解集
解集
数轴表示
数轴表示
解 法
解 法
实际应用
一、不等式的基本性质:
1)不等式两边都加上(或减去)同一个数
或同一个整式,不等号的方向____.
2)不等式两边都乘以(或除以)同一个
正数,不等号的方向____.
3)不等式两边都乘以(或除以)同一个
负数,不等号的方向____.
另外:不等式还具有______性.
如:当a>b, b>c时,则a>c
不变
不变
改变
记住哦!
传递
解一元一次不等式和解一元一次方程类似,有
①去分母 ②去括号 ③移项 ④ 合并同类项
⑤系数化为1等步骤.
它们的区别在哪里呢?
在系数化为1的这一步中,要特别注意
不等式的两边都乘以(或除以)一
个负数时,不等号的方向必须改变方向.
1、一元一次不等式的解法
二、方法与过程
2、一元一次不等式组的解法
(1)、先分别求出不等式组中各个不等式的解集。
(2)、利用数轴找出各个不等式的 解集的公共部分。
(3)、写出不等式组的解集。
特别注意:用数轴表示不等式的解集时,” <、>“用空心,” ≤、≥“用实心。” >、≥“向右画,” <、≤“向左画。
3、用一元一次不等式(组)解决实际问题的步骤:
①实际 问题(审题)
②设一个未知数(设元)
③列不等式(组)
④解不等式(组)
⑤检验解是否符合情况
三、题型大揭秘
(一)、用定义解题
⒈下列不等式中,是一元一次不等式的( )。
2.若
是关于x的一元一次不等式,则
该不等式的解集为:
D
(二)、数轴题
1、a,b两个实数在数轴上的对应点如图所示,用“<”或“>”号填空:
a__b; |a|____|b|; a+b___0 a-b__0; a+b___a-b;
2.一个不等式的解集如图所示,则这个不等式的正整数解是________.
(三)利用不等式性质进行同等变换
1、与2x<6不同解的不等式是( )
A.2x+1<7 B.4x<12
C.-4x>-12 D.-2x<-6
2、如果m<n<0,那么下列结论中错误的是( )
A、m-9<n-9 B、-m>-n
D、
C、
(四)限制条件的解
1.不等式3(x-2)≤x+4的非
负整数解有几个.( )
A.4 B.5 C.6 D.无数个
2.如果3+2x是正数,
则x的取值范围是_____,
如果3+2x是非负数,则
x的取值范围是________.
(五)已知解集求范围
1.若(a-1)x
C、a<1 D、a>1
2.关于x的方程5-a(1-x)=8x-(3-a)x的解是负数,则a的取值范围是( )
A、a<-4 B、a>5
C、a>-5 D、a<-5
3、如果不等式4x-3a>-1与不等式
2(x-1)+3>5的解集相同,请确定a的值.
(六)求不等式的特殊解
1.求x+3<6的所有正整数解。
解:x<3
∴ x+3<6的正整数解为1、2
2.求10-4(x-3)≥2(x-1)的非负整数解,并在数轴上表示出来。
3、若不等式2x-a>x的唯一负整数解释-1,
则a的取值范围是?
(七)确定方程或不等式中的字母及
应用中取值范围
1、在平面直角坐标系中若点P(m-3,m+1)在第二象限,则m的取值范围为( )
A.-1<m<3 B.m>3
C.m<-1 D.m>-1
2、已知关于x的方程
的解是非负整数,求m的取值范围?
(八)由解集求最值
1、若3x+4≤6+2(x-2),则x+1的
绝对值的最小值是多少?
2、已知关于x的不等式组
{
X-a≥0
5-2x>1
,只有5个整数解,则a的
取值范围是多少?
(九)实际问题与不等式(组)
Ⅰ、借不等式解不定方程。(方案问题)
七年级某班为了奖励学习进步的学生,购买了
单价为3元的笔记本和单价为5元的钢笔两种
奖品共花费了35元,则有几种购买方案?
解:设购买了单价为3元的笔记本m本,
购买了单价为5元的钢笔n支。则由题意列
方程:
3m+5n=35
∴
m=7-0.6m
因为m 和n是正整数
所以n=7- 0.6m为正整数,
则 0.6m为小于7的正整数,
可知m为5的倍数
∴{
m>0
.
∴
7- 0.6m>0
所以 m=5或者10
则n=4或者1
答:有2种购买方案①购买笔记本5本,钢笔4支
②购买笔记本10本,购买钢笔1支。
0
某单位给某小学捐献一批饮用水和蔬菜共320件
,其中饮用水比蔬菜多80件。
(1)求捐献了饮用水和蔬菜个多少件?
(2)现在计划用甲乙两种汽车共八辆一次性运输
这批饮用水和蔬菜到某小学。已知每辆甲种车最
多可装40件应用水和10件蔬菜,每辆已种汽车最
多能装饮用水和蔬菜各20件。已知每辆甲种货车
付运费400元,乙种货车副运费360元则可以有几
种方案来安排甲乙两种货车运输?哪种方案花费
最少?
解 (1)设饮用水x件,蔬菜y件。
根据题意列方程组,得
{
x+y=320
x-y=80
解,得
{
x=200
y=120
答:饮用水和蔬菜分别为200件和120件。
(2)设租用甲种车m辆,则租用乙种车(8-m)辆
依据题意,得
{
40m+20(8-m) ≥200
10m+20(8-m) ≥120
解,得2≤m≤4
因为m为正整数,所以m=2、3、4
所以安排甲乙两种车的时候有三种方案:
①甲种车2辆,乙种车6辆;
②甲种车3辆,乙种车5辆;
③甲种车4辆,乙种车4辆。
三种方案的运输费为:
①2×400+6×360=2960(元)
②3×400+5×360=3000(元)
③4×400+4×360=3040 (元)
所以使用第一种方案所用的方案运费最少为2960元。
所以应选择2辆甲种车,6辆乙种车。
总结:
从此例题种可看出,列不等式组解决方案问题
的思路一般是:
1、列出不等式组求出解集;
2、根据问题的实际意义确定出不等式组的一些
特殊解;
3、找出相应的可行性方案;
4、通过计算、比较,确定出最优方案。
{
课后练习:
1、将一批货物装箱,若每箱装8小包,则最后
一箱还差3包;若每箱装5包,则剩余的货物大于9包
且小于17包。这些货物共有多少个小包?多少个箱子?
2、若不等式组
{
3x-4≤0
X-a≥0
无解,则a的取值范围是?
