人教版九年级下册数学第28章锐角三角函数28.2解直角三角形的应用坡度、坡角-课件(共14张ppt)
文档属性
| 名称 | 人教版九年级下册数学第28章锐角三角函数28.2解直角三角形的应用坡度、坡角-课件(共14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 18:32:21 | ||
图片预览

文档简介
——坡度、坡角
解直角三角形的应用
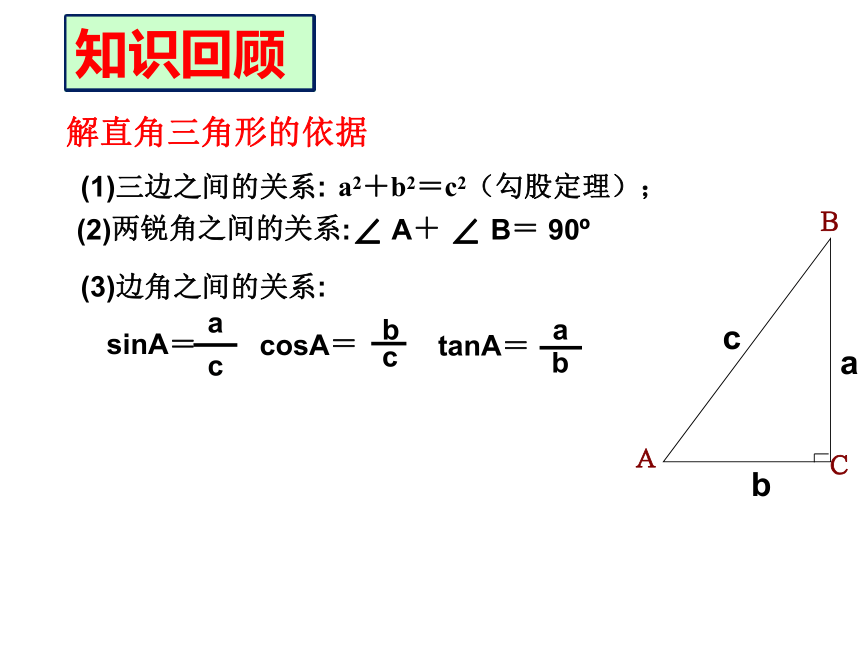
(1)三边之间的关系:
a2+b2=c2(勾股定理);
解直角三角形的依据
(2)两锐角之间的关系:∠ A+ ∠ B= 90?
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
A
C
B
a
b
c
知识回顾
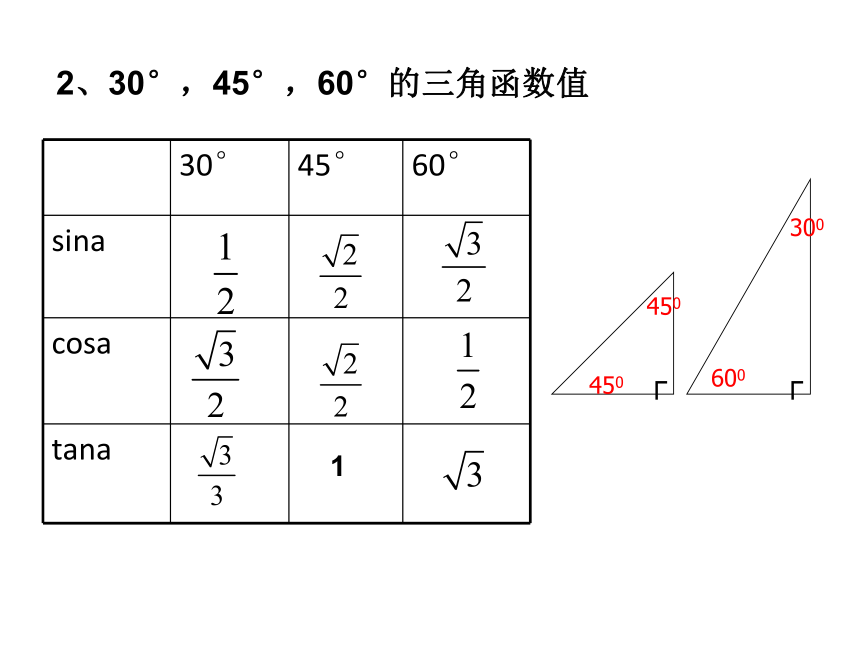
2、30°,45°,60°的三角函数值
30°
45°
60°
sina
cosa
tana
1
┌
┌
450
450
300
600
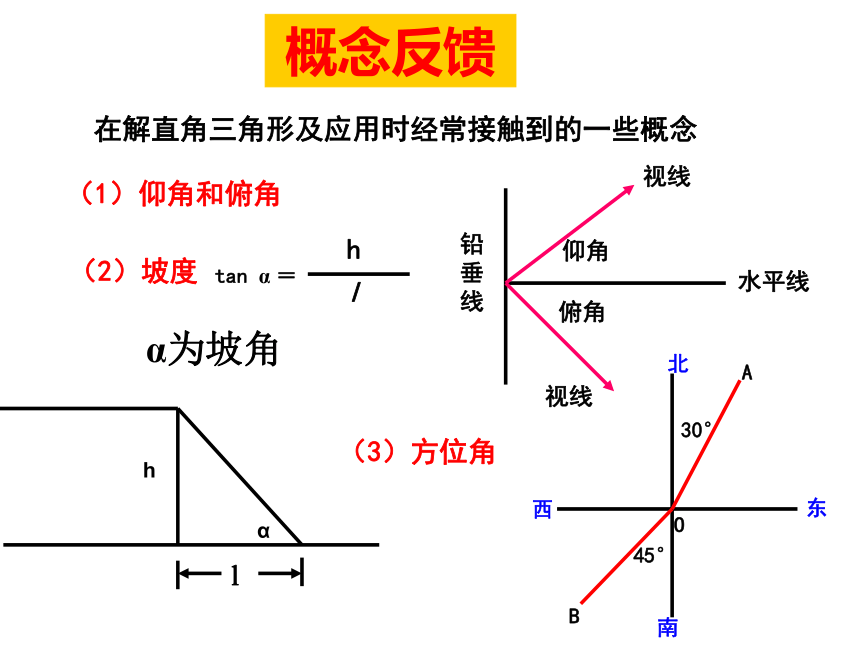
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
铅垂高度(h)
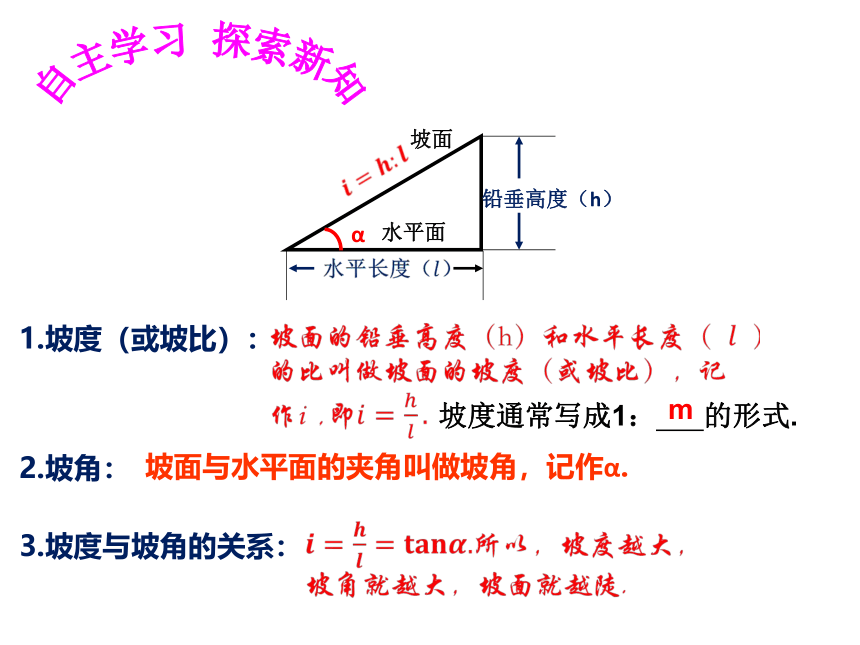
1.坡度(或坡比):
2.坡角:
坡面与水平面的夹角叫做坡角,记作α.
α
3.坡度与坡角的关系:
坡度通常写成1: 的形式.
m
自主学习 探索新知
坡面
水平面
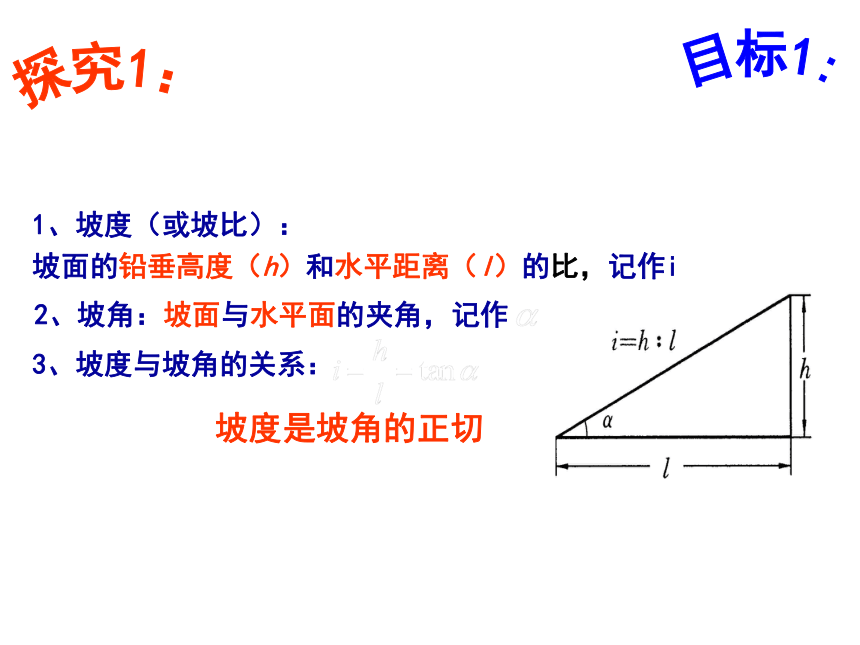
1、坡度(或坡比):
坡面的铅垂高度(h)和水平距离(l)的比,记作i
2、坡角:坡面与水平面的夹角,记作
3、坡度与坡角的关系:
探究1:
目标1:
坡度是坡角的正切
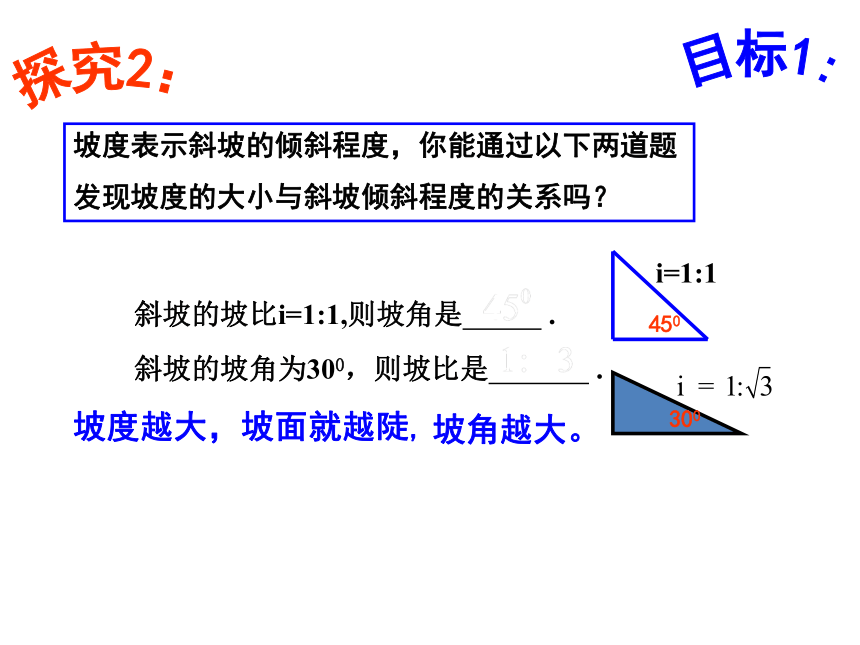
斜坡的坡比i=1:1,则坡角是 .
斜坡的坡角为300,则坡比是 .
坡度越大,坡面就越陡,
300
i=1:1
450
探究2:
坡度表示斜坡的倾斜程度,你能通过以下两道题
发现坡度的大小与斜坡倾斜程度的关系吗?
坡角越大。
目标1:
课堂达标
1、如图所示,堤高BC=1米,迎
水坡AB的长为2米,则斜坡AB的
坡度i= 。
2、如图,水坝横断面是梯形
ABCD,坝顶宽BC为3米,坝高4
米,斜坡AB长5米,斜坡CD的坡
度i=1:1,则坝底AD的长为
米。
B
C
A
B
C
A
D
10
1、斜坡的坡度是 ,则坡角α=______度。
2、斜坡的坡角是450 ,则坡比是 _______。
3、斜坡长是12米,坡高6米,则坡比是_____。
α
L
h
30
巩固概念
1:1
课堂小结
1.将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形问题);
2.根据条件的特点,适当选用锐角三角函数,应用直角三角形的有关性质,解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
1. 坡比、坡角的概念及其应用,特别是:
i=
=tanα
它体现了坡比和坡角间的关系.
2.
课堂小结
4.
3.
解直角三角形的应用
(1)三边之间的关系:
a2+b2=c2(勾股定理);
解直角三角形的依据
(2)两锐角之间的关系:∠ A+ ∠ B= 90?
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
A
C
B
a
b
c
知识回顾
2、30°,45°,60°的三角函数值
30°
45°
60°
sina
cosa
tana
1
┌
┌
450
450
300
600
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
铅垂高度(h)
1.坡度(或坡比):
2.坡角:
坡面与水平面的夹角叫做坡角,记作α.
α
3.坡度与坡角的关系:
坡度通常写成1: 的形式.
m
自主学习 探索新知
坡面
水平面
1、坡度(或坡比):
坡面的铅垂高度(h)和水平距离(l)的比,记作i
2、坡角:坡面与水平面的夹角,记作
3、坡度与坡角的关系:
探究1:
目标1:
坡度是坡角的正切
斜坡的坡比i=1:1,则坡角是 .
斜坡的坡角为300,则坡比是 .
坡度越大,坡面就越陡,
300
i=1:1
450
探究2:
坡度表示斜坡的倾斜程度,你能通过以下两道题
发现坡度的大小与斜坡倾斜程度的关系吗?
坡角越大。
目标1:
课堂达标
1、如图所示,堤高BC=1米,迎
水坡AB的长为2米,则斜坡AB的
坡度i= 。
2、如图,水坝横断面是梯形
ABCD,坝顶宽BC为3米,坝高4
米,斜坡AB长5米,斜坡CD的坡
度i=1:1,则坝底AD的长为
米。
B
C
A
B
C
A
D
10
1、斜坡的坡度是 ,则坡角α=______度。
2、斜坡的坡角是450 ,则坡比是 _______。
3、斜坡长是12米,坡高6米,则坡比是_____。
α
L
h
30
巩固概念
1:1
课堂小结
1.将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形问题);
2.根据条件的特点,适当选用锐角三角函数,应用直角三角形的有关性质,解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
1. 坡比、坡角的概念及其应用,特别是:
i=
=tanα
它体现了坡比和坡角间的关系.
2.
课堂小结
4.
3.
