人教版七年级数学下册 8.2.1用代入消元法解二元一次方程组 课件 (共23张PPT)
文档属性
| 名称 | 人教版七年级数学下册 8.2.1用代入消元法解二元一次方程组 课件 (共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 20:09:32 | ||
图片预览








文档简介
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
复 习 提 问
1、什么是二元一次方程,什么是二元一 次 方程组?
2、什么是二元一次方程的解?
3 、什么是二元一次方程组的解?
1、已知方程是 是二元一次方程
(1)求m,n;
(2)当方程中x=-2时,求出方程的解;
(3)这个二元一次方程有多少解?
2、写出一个二元一次方程,使它的解是
问题重现,探究解法
篮球联赛中,每场都要分出胜负,每队胜一场得2分,负一场得1分,某队为了争取较好的名次,想在全部的22场比赛中得到40分,那么这个队胜负应该分别是多少?
解法2:设胜x场,负(22-x)场.
2x+(22-x)=40
解法1:设胜x场,负y场
x+y=22 (1)
2x+y=40 (2 )
思考:上面的二元一次方程组和一元一次方程有什么关系?
设篮球队胜了x场,负了y场.
根据题意得方程组
x+y = 22
2x+y = 40
解:设胜x场,则负(22-x)场,根据题意得方程
2x+ (22-x) =40
解得 x=18
22-18=4
答:这个队胜18场,只负4场.
①
②
由①得,
y = 4
③
把③ 代入② ,得
2x+ (22-x) = 40
解这个方程,得
x=18
把 x=18 代入③ ,得
所以这个方程组的解是
y = 22-x
x=18
y = 4.
这样的形式叫做“用 x 表示 y”. 记住啦!
上面的解方程组的基本思路是什么?基本步骤有哪些?
上面解方程组的基本思路是“消元”——把“二元”变为“一元”。
主要步骤是:将其中的一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法。
及时归纳 ?
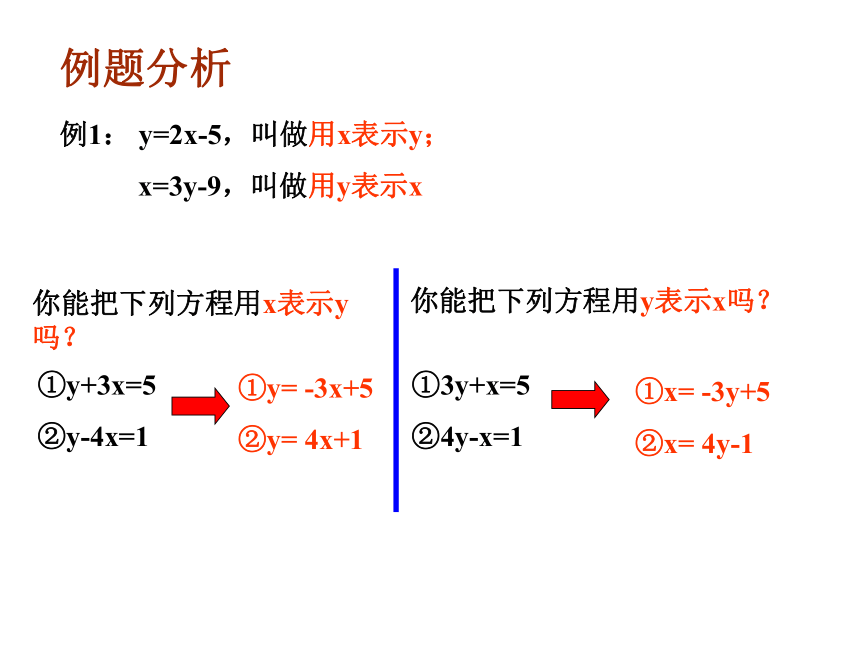
例1: y=2x-5,叫做用x表示y;
x=3y-9,叫做用y表示x
你能把下列方程用x表示y吗?
①y+3x=5
②y-4x=1
①y= -3x+5
②y= 4x+1
你能把下列方程用y表示x吗?
①3y+x=5
②4y-x=1
①x= -3y+5
②x= 4y-1
例题分析
练习(课本93页)
1、把下列方程改写成用含x的式子表示y的形式:
(1)2x-y=3; (2)3x+y-1=0
例2 解方程组
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴原方程组的解为
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值再代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
例2 解方程组
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴原方程组的解为
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值再代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
可以由②求出x再代入 ①吗?
可以把③代入② 求出x吗?
可以把x=3代入 ①或②求出y吗?
比一比,看哪组同学最快解下列方程组!
2、
3x+2y=14 ①
x — y = 3 ②
1、
y = 2x ①
x+y=12 ②
解:①将代入②,得
x+2x=12
3x=12
x=4
将x=4代入①,得
y=8
∴原方程组的解为
x=4
y=8
解:由 ②得 x=y+3 ③,
把③代入①得:
3(y+3)+2y=14
5y=5
y=1
将y=1代入② ,得
x=4
∴原方程组的解为
x=4
y=1
你做对了吗?
课堂学练:
2、用代入法解下列方程组(课本)
①
y = 2x-3
3x+2y=8
3x+2y=2
2x — y = 5
②
例1 根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:你能找出题目中的等量关系吗?
大瓶装:小瓶装=2:5
大瓶所装消毒液+小瓶所装消毒液=总生产量
解:设这些消毒液应该分装x大瓶,y小瓶,依题意得
①
②
试着解方程组
二元一次方程组
5x=2y
变形
500x+250y=22 500 000
用 代替y,消去未知数y
消去y
解得y
y=50 000
x=20 000
解 得 x
代 入
练习
3、有48支队520名运动员参加篮球、排球比赛,其中每只篮球队10人,每只排球队12人,每名运动员只能参加一项比赛。篮球、排球队各有多少支参赛?
4、张翔从学校出发骑自行车去县城,中途因道路施工步行一段路,1.5h后到达县城。他骑车的平均速度是15km/h,步行的平均速度是5km/h,路程全长20km.他骑车与步行各用多少时间?
试一试: 用代入法解
二元一次方程组
最为简单的方法是将________式中的
_________表示为__________,
再代入__________
①
x
X=6-5y
②
①
②
你知道整体代入吗?
解方程组
1、解二元一次方程组
⑴
x+y=5 ①
x-y=1 ②
⑵
2x+3y=40 ①
3x -2y=-5 ②
2、已知(2x+3y-4)+∣x+3y-7∣=0
则x= ,y= 。
2
-3
—
10
3
3、若方程
是关于x、y的二元一次方程,
求 的值。
做一做
探究:对于x+2y=5,思考下列问题:
(1)用含y的式子表示x;
(2)用含x的式子表示y;
x=1
y=2
x=3
y=1
x=5
y=0
(3)在自然数范围内方程的解是
x = 5 – 2y
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中的相应未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
本 课 小 结
再 见
作业:学评P76---78
——法国数学家 笛卡儿[Descartes, 1596-1650 ]
复 习 提 问
1、什么是二元一次方程,什么是二元一 次 方程组?
2、什么是二元一次方程的解?
3 、什么是二元一次方程组的解?
1、已知方程是 是二元一次方程
(1)求m,n;
(2)当方程中x=-2时,求出方程的解;
(3)这个二元一次方程有多少解?
2、写出一个二元一次方程,使它的解是
问题重现,探究解法
篮球联赛中,每场都要分出胜负,每队胜一场得2分,负一场得1分,某队为了争取较好的名次,想在全部的22场比赛中得到40分,那么这个队胜负应该分别是多少?
解法2:设胜x场,负(22-x)场.
2x+(22-x)=40
解法1:设胜x场,负y场
x+y=22 (1)
2x+y=40 (2 )
思考:上面的二元一次方程组和一元一次方程有什么关系?
设篮球队胜了x场,负了y场.
根据题意得方程组
x+y = 22
2x+y = 40
解:设胜x场,则负(22-x)场,根据题意得方程
2x+ (22-x) =40
解得 x=18
22-18=4
答:这个队胜18场,只负4场.
①
②
由①得,
y = 4
③
把③ 代入② ,得
2x+ (22-x) = 40
解这个方程,得
x=18
把 x=18 代入③ ,得
所以这个方程组的解是
y = 22-x
x=18
y = 4.
这样的形式叫做“用 x 表示 y”. 记住啦!
上面的解方程组的基本思路是什么?基本步骤有哪些?
上面解方程组的基本思路是“消元”——把“二元”变为“一元”。
主要步骤是:将其中的一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法。
及时归纳 ?
例1: y=2x-5,叫做用x表示y;
x=3y-9,叫做用y表示x
你能把下列方程用x表示y吗?
①y+3x=5
②y-4x=1
①y= -3x+5
②y= 4x+1
你能把下列方程用y表示x吗?
①3y+x=5
②4y-x=1
①x= -3y+5
②x= 4y-1
例题分析
练习(课本93页)
1、把下列方程改写成用含x的式子表示y的形式:
(1)2x-y=3; (2)3x+y-1=0
例2 解方程组
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴原方程组的解为
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值再代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
例2 解方程组
3x – 2y = 19
2x + y = 1
解:
①
②
3x – 2y = 19
2x + y = 1
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴原方程组的解为
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值再代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
可以由②求出x再代入 ①吗?
可以把③代入② 求出x吗?
可以把x=3代入 ①或②求出y吗?
比一比,看哪组同学最快解下列方程组!
2、
3x+2y=14 ①
x — y = 3 ②
1、
y = 2x ①
x+y=12 ②
解:①将代入②,得
x+2x=12
3x=12
x=4
将x=4代入①,得
y=8
∴原方程组的解为
x=4
y=8
解:由 ②得 x=y+3 ③,
把③代入①得:
3(y+3)+2y=14
5y=5
y=1
将y=1代入② ,得
x=4
∴原方程组的解为
x=4
y=1
你做对了吗?
课堂学练:
2、用代入法解下列方程组(课本)
①
y = 2x-3
3x+2y=8
3x+2y=2
2x — y = 5
②
例1 根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
分析:你能找出题目中的等量关系吗?
大瓶装:小瓶装=2:5
大瓶所装消毒液+小瓶所装消毒液=总生产量
解:设这些消毒液应该分装x大瓶,y小瓶,依题意得
①
②
试着解方程组
二元一次方程组
5x=2y
变形
500x+250y=22 500 000
用 代替y,消去未知数y
消去y
解得y
y=50 000
x=20 000
解 得 x
代 入
练习
3、有48支队520名运动员参加篮球、排球比赛,其中每只篮球队10人,每只排球队12人,每名运动员只能参加一项比赛。篮球、排球队各有多少支参赛?
4、张翔从学校出发骑自行车去县城,中途因道路施工步行一段路,1.5h后到达县城。他骑车的平均速度是15km/h,步行的平均速度是5km/h,路程全长20km.他骑车与步行各用多少时间?
试一试: 用代入法解
二元一次方程组
最为简单的方法是将________式中的
_________表示为__________,
再代入__________
①
x
X=6-5y
②
①
②
你知道整体代入吗?
解方程组
1、解二元一次方程组
⑴
x+y=5 ①
x-y=1 ②
⑵
2x+3y=40 ①
3x -2y=-5 ②
2、已知(2x+3y-4)+∣x+3y-7∣=0
则x= ,y= 。
2
-3
—
10
3
3、若方程
是关于x、y的二元一次方程,
求 的值。
做一做
探究:对于x+2y=5,思考下列问题:
(1)用含y的式子表示x;
(2)用含x的式子表示y;
x=1
y=2
x=3
y=1
x=5
y=0
(3)在自然数范围内方程的解是
x = 5 – 2y
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数(变形)
2、用这个一次式代替另一个方程中的相应未知数,得到一个一元一次方程,求得一个未知数的值(代入求解)
3、把这个未知数的值代入一次式,求得另一个未知数的值(再代求解)
4、写出方程组的解(写解)
用代入法解二元一次方程组的一般步骤
解二元一次方程组
用代入法
本 课 小 结
再 见
作业:学评P76---78
