人教版七年级数学下册 8.2.2用加减消元法解二元一次方程组 课件 (共15张PPT)
文档属性
| 名称 | 人教版七年级数学下册 8.2.2用加减消元法解二元一次方程组 课件 (共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览






文档简介
课前训练、用代入法解下列方程组
①
y = 2x-3
3x+2y=8
3x+2y=2
2x — y = 5
②
学习目标
1.会用加减法求未知数系数相等或互为相反数的二元一次方程组的解。
2.通过探求二元一次方程组的解法,经历用加减法把 “二元”化为“一元”的过程,体会消元的思想,以及把“未知”转化为“已知”,把复杂问题转化为简单问题的化归思想.
3.重点:用加减法解二元一次方程组.
4.难点:两个方程相减消元时,对被减的方程各项符号要做变号处理。
你能想到多少种方法解右边的二元一次方程组?
②-①,得 x=18
把x=18代入①,得 y=4
① - ②也能消去y,求得x吗?
①
②
问题再现,再探解法
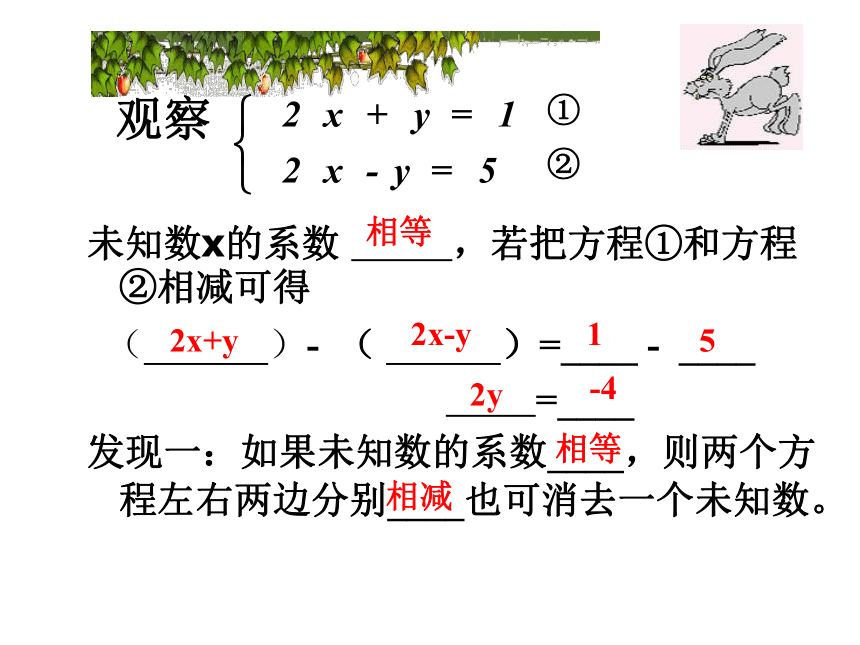
未知数x的系数 ,若把方程①和方程②相减可得
( )- ( )=____ - ____
=____
发现一:如果未知数的系数____,则两个方程左右两边分别____也可消去一个未知数。
观察
①
②
相等
2x+y
2y
相等
相减
2x-y
1
5
-4
观察
①
②
未知数y的系数 _______,若把方程(1)和方程(2)相加可得
( )+ ( )=____ + ____
=____
发现二:如果未知数的系数互为_______则两个方程左右两边分别____ 可以消去一个未知数.
互为相反数
2x+y
2x-y
1
5
4x
6
相加
相反数
【归纳】
两个二元一次方程组中,同一个未知数的系数______ 或 _________ 时,把这两个方程的两边分别 ______ 或 _____ ,就能消去这个未知数,得到一个_________方程,这种方法就叫做加减消元法,简称加减法。
相等
互为相反数
相减
相加
一元一次
联系上面的解法,想一想怎样解方程组
①
②
解:①+②,得
19x=38
解得 x=2
把x=2代入①得 4×2+10y=30
解得 y=2.2
x=2
故这个方程组的解是 y=2.2
代入②呢?
第一步:加减求解
第二步:代入求解
第三步:写解
用加减法解方程组
①
②
方程中没有同一个未知数的系数是相反或者相同,直接加减,能消去某个未知数吗?如果不能,怎么办呢?
解:①×3,得 9x+12y=48 ③
②×2,得 10x-12y=66 ④
③+④,得 19x=114
解得 x=6
把x=6代入①,得 3×6+4y=16
解得
所以这个方程组的解是
代入②呢?
能否通过变形,使得两个方程中某个未知数的系数相反或者相同
先消去X,应该如何解?
方程变形的依据是什么?
第一步:变形
第二步:加减求解
第三步:代入求解
第四步:写解
练习:
1、用加减法解下列方程组:
例4、 2台大收割机和5台小收割机均工作2小时共收割小麦3.6公顷,3台大收割机和2台小收割机均工作5小时共收割小麦8公顷。1台大收割机和1台小收割机每小时各收割下麦多少公顷?
分析:若1台大收割机每小时收割x公顷,1台小收割机每小时收割y公顷
2台大收割机和5台小收割机均工作1小时收割小麦 公顷3台大收割机和2台小收割机均工作1小时收割小麦 公顷
解:设1台大收割机每小时收割x公顷,1台小收割机每小时收割y公顷 ,依题意得
①
②
(2x+5y)
(3x+2y)
练习:
2、一条船顺流航行,每小时行20km;逆流航行,每小时
行16km.求轮船在静水中的速度与水流的速度。
3、运输360t化肥,装载了6节火车车厢和15辆汽车;运
输440t化肥,装载了8节火车车厢和10辆汽车。每节火车
车厢与每辆汽车平均各装多少吨化肥?
用加减消元法解二元一次方程组的一般步骤:
第一步:在所解的方程组的两个方程中,如果某个未知数的系数互为相反数,
可以把这两个方程的两边分别相加,消去这个未知数;
如果未知数的系数相等,可以直接把两个方程两边相减,消去这个未知数。
第二步:如果方程组中不存在
某个未知数的系数绝对值相等,
那么应选出一组系数
(选最小公倍数较小的一组系数)
求出它们的最小公倍数
(如果一个系数是另一个系数的整倍,
该系数即为最小公倍数),
然后将原方程变形,
使新方程组的同一个
未知数系数的绝对值相等
(都等于原系数的最小公倍数),
再加减消元。
作业:《学评》P78-80
①
y = 2x-3
3x+2y=8
3x+2y=2
2x — y = 5
②
学习目标
1.会用加减法求未知数系数相等或互为相反数的二元一次方程组的解。
2.通过探求二元一次方程组的解法,经历用加减法把 “二元”化为“一元”的过程,体会消元的思想,以及把“未知”转化为“已知”,把复杂问题转化为简单问题的化归思想.
3.重点:用加减法解二元一次方程组.
4.难点:两个方程相减消元时,对被减的方程各项符号要做变号处理。
你能想到多少种方法解右边的二元一次方程组?
②-①,得 x=18
把x=18代入①,得 y=4
① - ②也能消去y,求得x吗?
①
②
问题再现,再探解法
未知数x的系数 ,若把方程①和方程②相减可得
( )- ( )=____ - ____
=____
发现一:如果未知数的系数____,则两个方程左右两边分别____也可消去一个未知数。
观察
①
②
相等
2x+y
2y
相等
相减
2x-y
1
5
-4
观察
①
②
未知数y的系数 _______,若把方程(1)和方程(2)相加可得
( )+ ( )=____ + ____
=____
发现二:如果未知数的系数互为_______则两个方程左右两边分别____ 可以消去一个未知数.
互为相反数
2x+y
2x-y
1
5
4x
6
相加
相反数
【归纳】
两个二元一次方程组中,同一个未知数的系数______ 或 _________ 时,把这两个方程的两边分别 ______ 或 _____ ,就能消去这个未知数,得到一个_________方程,这种方法就叫做加减消元法,简称加减法。
相等
互为相反数
相减
相加
一元一次
联系上面的解法,想一想怎样解方程组
①
②
解:①+②,得
19x=38
解得 x=2
把x=2代入①得 4×2+10y=30
解得 y=2.2
x=2
故这个方程组的解是 y=2.2
代入②呢?
第一步:加减求解
第二步:代入求解
第三步:写解
用加减法解方程组
①
②
方程中没有同一个未知数的系数是相反或者相同,直接加减,能消去某个未知数吗?如果不能,怎么办呢?
解:①×3,得 9x+12y=48 ③
②×2,得 10x-12y=66 ④
③+④,得 19x=114
解得 x=6
把x=6代入①,得 3×6+4y=16
解得
所以这个方程组的解是
代入②呢?
能否通过变形,使得两个方程中某个未知数的系数相反或者相同
先消去X,应该如何解?
方程变形的依据是什么?
第一步:变形
第二步:加减求解
第三步:代入求解
第四步:写解
练习:
1、用加减法解下列方程组:
例4、 2台大收割机和5台小收割机均工作2小时共收割小麦3.6公顷,3台大收割机和2台小收割机均工作5小时共收割小麦8公顷。1台大收割机和1台小收割机每小时各收割下麦多少公顷?
分析:若1台大收割机每小时收割x公顷,1台小收割机每小时收割y公顷
2台大收割机和5台小收割机均工作1小时收割小麦 公顷3台大收割机和2台小收割机均工作1小时收割小麦 公顷
解:设1台大收割机每小时收割x公顷,1台小收割机每小时收割y公顷 ,依题意得
①
②
(2x+5y)
(3x+2y)
练习:
2、一条船顺流航行,每小时行20km;逆流航行,每小时
行16km.求轮船在静水中的速度与水流的速度。
3、运输360t化肥,装载了6节火车车厢和15辆汽车;运
输440t化肥,装载了8节火车车厢和10辆汽车。每节火车
车厢与每辆汽车平均各装多少吨化肥?
用加减消元法解二元一次方程组的一般步骤:
第一步:在所解的方程组的两个方程中,如果某个未知数的系数互为相反数,
可以把这两个方程的两边分别相加,消去这个未知数;
如果未知数的系数相等,可以直接把两个方程两边相减,消去这个未知数。
第二步:如果方程组中不存在
某个未知数的系数绝对值相等,
那么应选出一组系数
(选最小公倍数较小的一组系数)
求出它们的最小公倍数
(如果一个系数是另一个系数的整倍,
该系数即为最小公倍数),
然后将原方程变形,
使新方程组的同一个
未知数系数的绝对值相等
(都等于原系数的最小公倍数),
再加减消元。
作业:《学评》P78-80
